作者:九三 来源:蒲公英
目前,国家在以市场机制倒逼企业的质量提升,怎么倒逼呢?市场大面积的抽检!近一段时间以来,国家局、省局乃至市局,大幅提高了对市场的抽检力度,各地各类企业都有各类产品被暴不合格。那么,这些不合格,是各企业放行销售时,没有进行相应的检测吗?应当不会,那么是怎么回事?想来,恐怕有两方面原因不能不提,
其一:抽样方案合适与否,是否有代表性?
其二:测量数据的质量如何?精确度如何?是否误差过大造成…等等?
抽样方案合适与否,生产方风险和使用方风险如何认识,在以前的文章中做过说明,这里不再重复;本次主要从第二个方面“测量数据质量如何?”来谈一下,测量分析系统中的重复性和再现性问题。
以数据(事实)为依据,来驱动管理的要求下,当如何看待数据呢?测量时的波动/误差(波动/误差的大小以其方差来表示的)有多大?是否满足相应产品工艺要求?不同检验员之间检验误差有多大,结果是否可以接受呢?下面,就此做一些讨论,希望大家拍砖,或对大家有些借鉴。
任何实测数据的波动都可以看作过程的波动和测量系统的波动/误差之和,如下面公式:

在本文中,对于生产过程的波动,暂不讨论;仅从测量系统分析看,影响其有6个方面问题,分别是:
分辨力、稳定性、偏倚和线性、重复性和再现性;
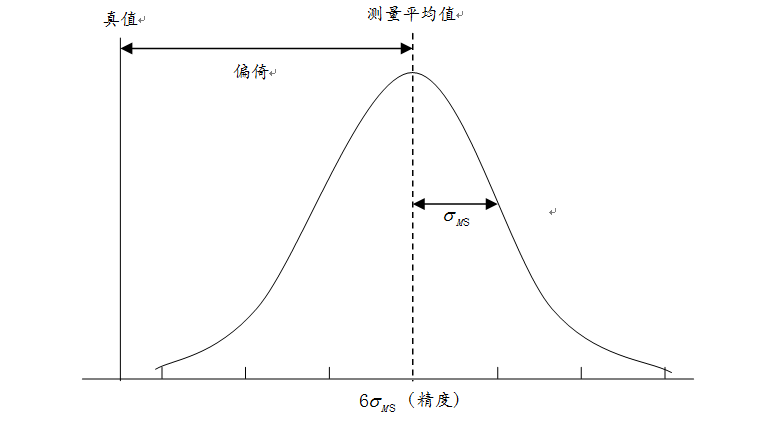
其中,偏倚是测量系统准确度的度量,用来描述测量结果的位置方面的状况,反映的是测量结果平均值与真值的差异程度;
重复性与再现性构成了测量系统的精度,用来描述测量结果的波动/误差状况。
一个测量系统是否足够好,它的关键指标有准确度(偏倚)和精度(重复性和再现性)两方面,其含义可以参见下图:
测量系统分析和计算思路如下: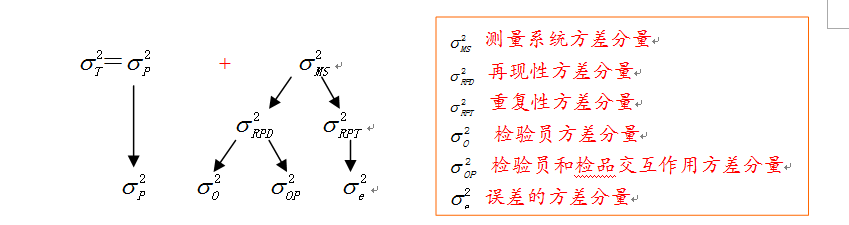
本文将通过一个例子,来讨论一下,精确度(重复性和再现性)对检测结果的影响,以及如何系统科学地考察,这个影响程度和大小,以及是否可以接受。
例:某个产品,标准要求检测相对密度,标准的范围是1.28~1.30。安排3名检验员,分别对10批次产品进行检测,并对这些数据进行MSA(测量分析系统)分析,数据如下:
批次 | 检验员 | 相对密度 | 批次 | 检验员 | 相对密度 | 批次 | 检验员 | 相对密度 |
2 | 1 | 1.2927 | 1 | 1 | 1.2958 | 8 | 3 | 1.2853 |
6 | 1 | 1.2895 | 10 | 2 | 1.2991 | 5 | 3 | 1.2827 |
3 | 1 | 1.2891 | 6 | 2 | 1.2889 | 3 | 3 | 1.2888 |
7 | 1 | 1.2908 | 5 | 2 | 1.2840 | 1 | 3 | 1.2940
|
4 | 1 | 1.2876 | 9 | 2 | 1.2960 | 7 | 3 | 1.2911 |
5 | 1 | 1.2834 | 7 | 2 | 1.2912 | 6 | 3 | 1.2891 |
10 | 1 | 1.3003 | 4 | 2 | 1.2872 | 10 | 3 | 1.2990 |
1 | 1 | 1.2937 | 3 | 2 | 1.2890 | 4 | 3 | 1.2864 |
8 | 1 | 1.2850 | 1 | 2 | 1.2941 | 9 | 3 | 1.2966 |
9 | 1 | 1.2945 | 2 | 2 | 1.2924 | 6 | 1 | 1.2861 |
2 | 2 | 1.2925
| 8 | 2 | 1.2851 | 4 | 1 | 1.2847 |
6 | 2 | 1.2888 | 4 | 3 | 1.2863 | 3 | 1 | 1.2873 |
5 | 2 | 1.2818 | 10 | 3 | 1.2993 | 8 | 1 | 1.2843 |
4 | 2 | 1.2847 | 1 | 3 | 1.2935 | 9 | 1 | 1.2945 |
3 | 2 | 1.2880 | 6 | 3 | 1.2893 | 5 | 1 | 1.2826 |
1 | 2 | 1.2936 | 7 | 3 | 1.2917 | 2 | 1 | 1.2922 |
8 | 2 | 1.2838 | 8 | 3 | 1.2856 | 10 | 1 | 1.2984 |
7 | 2 | 1.2910 | 9 | 3 | 1.2956 | 7 | 1 | 1.2904 |
10 | 2 | 1.2989 | 5 | 3 | 1.2837 | 2 | 3 | 1.2938 |
9 | 2 | 1.2946 | 2 | 3 | 1.2925 | 3 | 3 | 1.2892 |
相对密度的检测,其原理是以某物质与4℃时纯化水的密度进行比较而得,继而可以将体积这个相对大的误差项回避,进而,仅以质量项进行比较,公式如:ρ=m/v,则ρ相对=(m样)/(m水×0.99823);
利用minitab 17中统计/质量工具/量具研究/量具R&R研究(交叉),得如下方差分析结果:
量具 R&R 研究 - 方差分析法
包含交互作用的双因子方差分析表
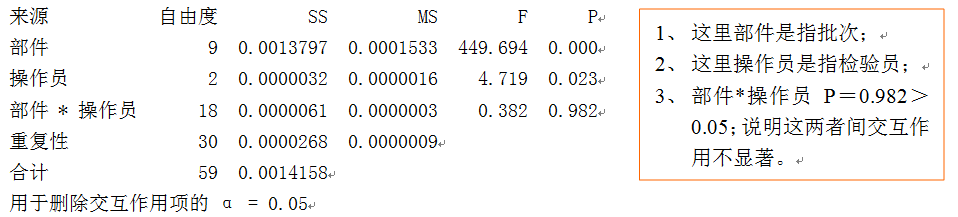
不包含交互作用的双因子方差分析表

量具 R&R
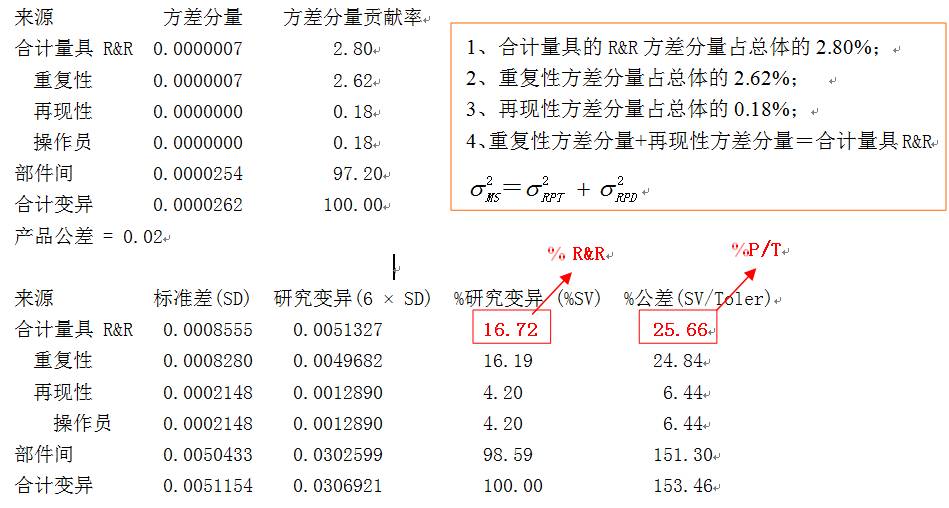
可区分的类别数(ndc) = 8
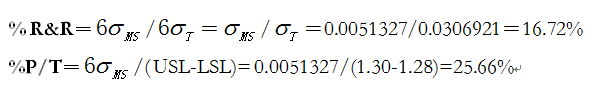
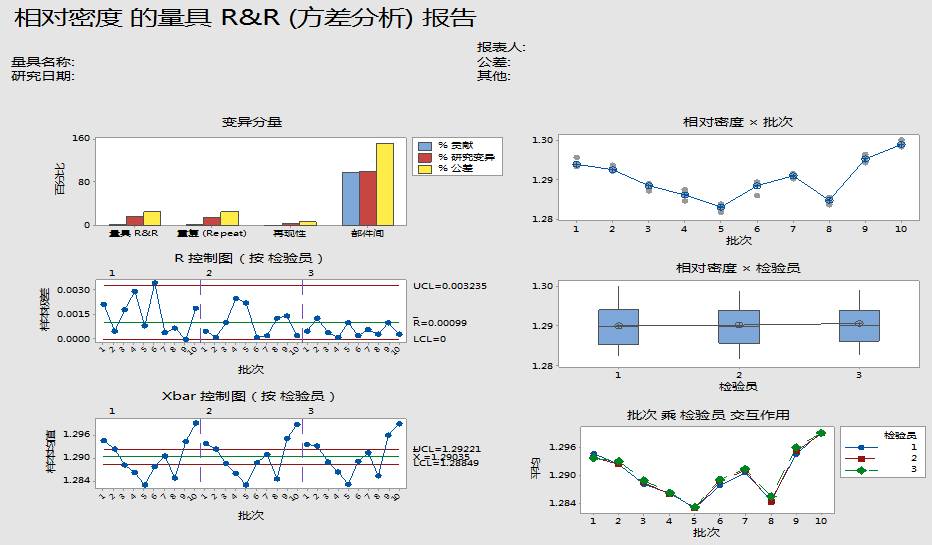
从上面的六合一图的报告卡可得:
1、左上图:
蓝色柱形的百分比贡献:批次间(部件)波动分量的方差与总体波动分量的方差之比占绝大部分(97.2%),说明批次间的波动是主要的。量具和重复性柱形分别为2.8%和2.62%(对应于10%~30%标准,此值应在1%~9%),也就是说,量具R&R柱形高度要小于1%,最好;视检验项目的重要程度,要在1%~9%之内,也是可接受的。
红色柱形的百分比研究变异:批次间(部件)波动分量的标准差与总体波动分量的标准差之比,即方差分析中的“%R&R”从图上看,量具R&R和重复性的柱形高度就比上面的蓝色的百分比贡献高多了,正如方差分析数据所示的分别达到了16.72%和16.19%。从测量分析来讲,介于10%~30%之间,测量系统可接受。
黄色柱形的百分比公差:批次间(部件)的波动分量巨大,说明批次的波动相对其公差0.02来讲是过大了;对于,该测量系统来说,0.02的公差有些小;如果这样小的公差设置是合适而必要的,且该项目相对于产品的安全性和有效性是重要的;那么,该测量系统需要做相应的改善和提高。同时,量具R&R为25.66%,重复性为24.84%;介于10%~30%之间,也说明该测量系统勉强可接受。
2、左中图:3个检验员中第1位有超上限点,可考虑对1号检验加强练习与考核;而第2、3位检验员,过程还可。不过本图在分析测量系统性能上,不是十分准确有效,供参考。
3、左下图:3个检验员的绝大多数平均值点落在控制域外,因为越多的数据点超出Xbar图的控制限,表明过程实际波动越大,同时该测量系统能力越好。不过本图在分析测量系统性能上,不是十分准确有效,供参考。
4、右上图:10批次检验结果运行图可以看出,其连线变化大,也说明其过程实际波动也大;而除第4、6批外,其它批均值周围的多个散点也分布集中,表明其重复性和再现性的波动较小。但需要对第4、6批的测量过程进行调查;本图对改进测量系统的工作有指导意义。
5、右中图:3个检验员检测的结果运行图,从图看,这条均值的连线变化小,比较平坦,表明再现性波动小。本图由于是平均结果,可能会将高低相差悬殊的点平均了,所以本图的参考价值小。
6、右下图:3个检验员10批次测量结果的均值的运行图,从图中可以看出,该连线上下波动大,也说明批次间过程波动大,3个检验员的3条连线接近平行,说明检验员与批次间的交互作用小,不显著。3个检验员在这个检验项目上,其水平相当。
结论:
1、可区分的类别数 ndc = 8≥5,表明测量系统的分辨力合格,能够用于过程参数的测量。
2、从测量系统占过程总波动看,% R&R=16.72%,介于10%~30%之间,小于20%,测量系统是可接受。
3、从测量系统占公差的百分比看,%P/T=25.66%,介于10%~30%之间,大于20%,小于30%,测量系统勉强可接受。
4、对于该测量系统来说,0.02的公差有些小;如果这样小的公差设置是合适而必要的,且该项目相对于产品的安全性和有效性是重要的;那么,该测量系统需要做相应的改善和提高。













