
要理解量子纠缠,首先先要明白一个概念。
什么是量子态。
我们先来看一个高中的物理实验。
我们知道光是电磁波,是有偏正的。
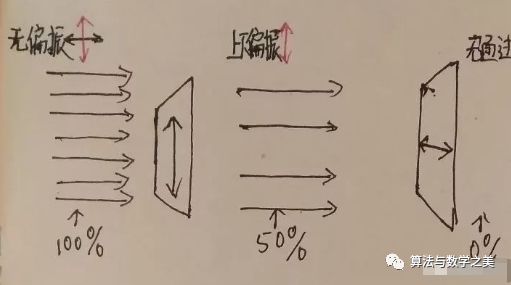
当一束光经过上下偏振的偏振之后,部分光就会被阻隔,只有一半的光会透过去,透过去的光就变成了上下偏振的了。这时候,你在末尾放一个左右偏振的偏振片,因为这时候的光完全是上下偏振的,所以就不会有任何光通过。
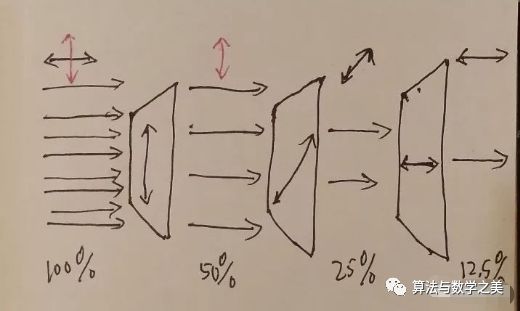
可是,假如说我们在两个偏振片中间再加一个比如说45度角的偏振片,那么反而最后会有50%*50%*50%=12.5%的光通过了最后的偏振片。
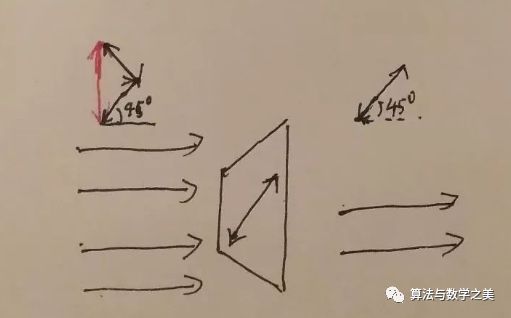
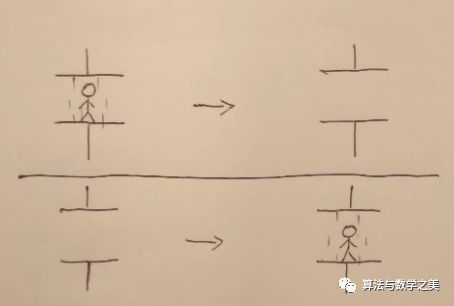
高中物理里的解释是,上下偏振的光可以看做如图两个垂直的偏振的和。所以通过45度斜角偏振的光只留下和偏振片方向相同的那个分量,而另一个分量被偏振片阻挡了。所以会有50%的光通过了这个偏振片。
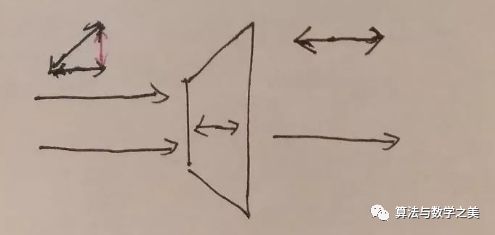
同理最后那个水平方向的偏振片让50%的45度斜方向偏振的光通过。
但是,以上高中知识对于偏振的理解是有不完善的。
首先,我们知道光的量子性,光的能量不是可以随便分的,而是有最小的单位,就是一个光子的能量。一束震动频率为v的光束,其光子的能量E=hv,其中h为普朗克常量。
我们再从光子的角度来看待上面的实验。
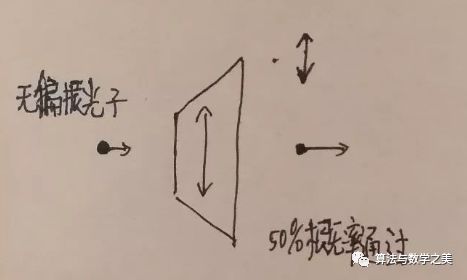
一个没有偏振方向的光子,50%的概率不能通过上下偏振片,50%的概率可以通过上下偏振片,通过后它就变成了上下偏振的光子。
对于单独一个光子来讲,要么就完全通过,要么就完全没有通过,并不存在说有一半通过了。
这就涉及到光子的量子态了。
对于一个没有偏振方向的光子,你可以把它看做是50%概率上下偏振和50%左右偏振的叠加,这个量子态可以记做
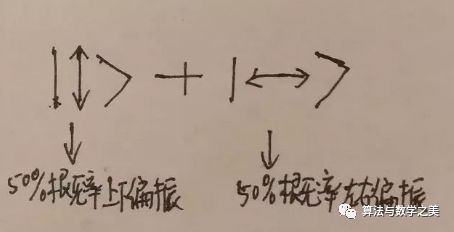
而当你要一个光子通过上下偏振片的时候,其实就是在对它进行一次测量,看它到底是处于哪一种状态,于是这个光子的量子态就会坍缩成一个确定的状态,50%的概率坍缩成上下偏振,50%的概率坍缩成左右偏振。
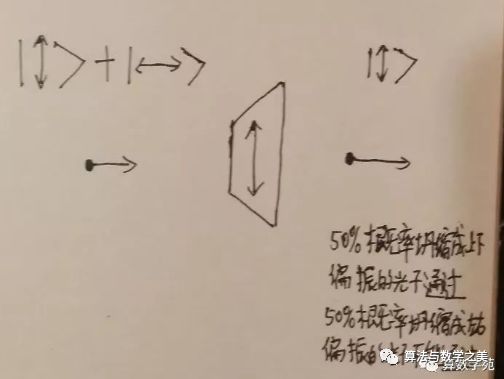
所以
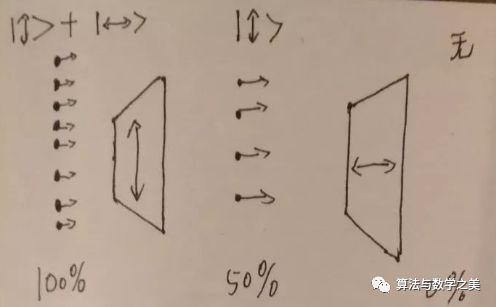
上面的实验一可以这么理解,有50%的光子坍缩成了上下偏振通过一个偏振片,这时候它所有的光子都是上下偏振,所以最后没有光子可以通过第二个偏振片。
在实验二里,
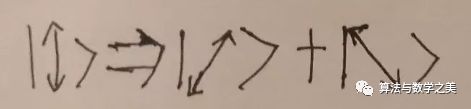
因为上下偏振的光子又可以看做是另两个相垂直的偏振方向的叠加。
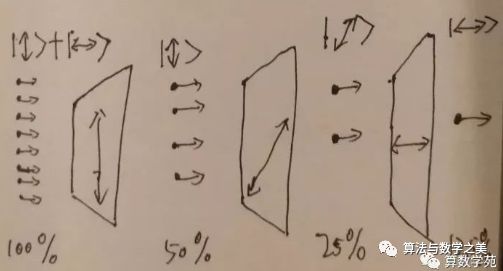
所以上下偏振的光子又有50%的概率坍缩成45度斜偏振的状态,通过第二块偏振片,同理最后又有50%的概率坍缩成左右偏振的光子,通过最后一块的偏振片。
假如说一共有1000个光子,那么最后平均通过所有偏振片的光子是125个。
现在回到量子纠缠。
先来看一个经典世界里面比较容易理解的例子。
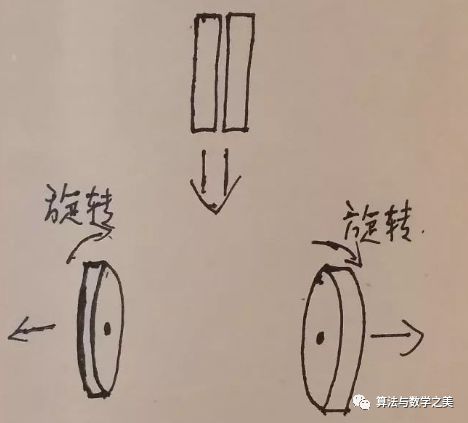
假如说在太空中两个挨在一起静止的相同圆盘,被一个炸弹炸开,它们两个开始有了一个旋转。
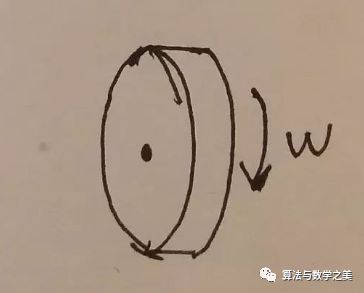
它们飞了很远之后,我们捕获了其中的一个圆盘,对它进行测量,发现它的旋转角速度为w,那么我立刻可以知道,另一个圆盘的角速度一定是-w,因为根据角动量守恒,两个圆盘的角动量之和一定是为零的,所以它们两个的旋转角速度一定是相反的。
而量子纠缠有些类似。
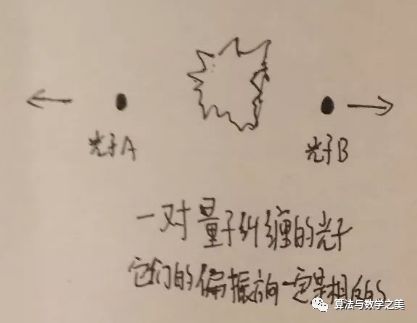
当一对有量子纠缠的光子,往相反方向飞了很远之后,我们捕获了其中的一个光子,测量得到它的偏振方向是逆时针偏振的(这是光偏振的一种,这里不需要具体理解)。那么立刻,我们可以知道在很远的另一个光子它的偏振方向是顺时针偏振的。因为根据量子纠缠我们知道它们两个的偏振方向一定是相反的。
看到这里,有人就会觉得说,那么量子纠缠看上去并没有什么特别的呀。那么为什么会被讨论的那么多?
前面两种情况,量子纠缠的实验和前面那个经典世界里面的实验区别在哪里呢?
最主要的一个区别就是,经典世界里面,在爆炸之后的那一瞬间,两个圆盘的状态就已经是确定了的,只是在于说我们什么时间去测量,无论在什么时间和位置去测量,得到的都会是同样的结果。

可是,在量子纠缠的实验里面,两个光子往相反方向飞行的途中,其中每一个光子的偏振方向并不是确定的,而是处于50%的概率顺时针偏振和50%逆时针偏振相叠加的量子态。
就是说,你测量的结果有50%的概率是顺时针偏振,有50%的概率是逆时针偏振。这个光子的状态只有在你测量的时候才能确定,而且完全是一个概率性事件。
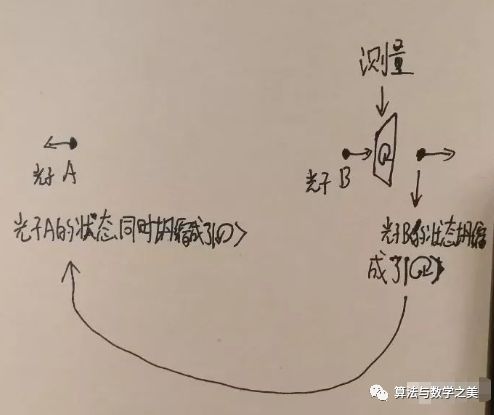
就是说,你测量了其中一个光子,这一个光子的状态坍缩成了比如说顺时针偏振。在遥远地方的另一个光子它的状态就同时坍缩成了确定的逆时针偏振,仿佛这两个光子间有一个可以超越光速的联系,可以让它们瞬间可以达成共识。
但是当然,其实并没有存在说超越光速的信息传递。量子纠缠并不能用作超光速通信,而是只能作为一种加密的手段。这又是另一故事了。
那怎么来解释量子纠缠这一现象呢?
额,其实这根本不需要解释。首先这一现象的提出是物理学家在对量子物理学里面的东西进行计算的时候得出来的,就是说是完全先由纯数学的计算得出的结论,然后物理学家们觉得这一结论太不可思议了,所以才反复进行了讨论,最后实验得到的结果却证实了量子纠缠这一现象。
其实就是说,这一现象本身就是这个宇宙运行的规则,只是因为不符合我们人类一般的思维习惯,所以才会被觉得奇怪。
————
编辑 ∑Pluto
来源:算数学苑
更多精彩:
☞泰勒定理的奇闻轶事
☞丘成桐:漫谈微分几何
☞Leibniz 如何想出微积分?(一)
☞线性相关和秩的物理意义
☞数学史上你认为最丑陋的公式是什么?
☞陶哲轩谈什么是好的数学
☞田渊栋:数学的用处(下篇)
☞你绝对没想过原来数学家这么流氓,一言不合就进行暴力证明
☞世界上最牛的五篇博士论文
☞数学中有哪些巧合让人眼前一亮?
☞算法立功!清华毕业教授美国被抢车,警察无能为力自己用“贪心算法”找回
☞学术史上的奇文:怎样用数学抓狮子
☞台大教授的反思:最难的一课 我们却没教给学生
☞麻省理工学院(MIT)研究生学习指导—— 怎样做研究生
☞分享 数学,常识和运气 ——投资大师詹姆斯·西蒙斯2010年在MIT的讲座
算法数学之美微信公众号欢迎赐稿
稿件涉及数学、物理、算法、计算机、编程等相关领域,经采用我们将奉上稿酬。
投稿邮箱:[email protected]















