(点击上方公众号,可快速关注)
来源: 英雄哪里出来
cppblog.com/menjitianya/archive/2015/10/23/212084.html
如有好文章投稿,请点击 → 这里了解详情
四、动态规划和数据结构结合的常用优化
1、滚动数组
【例题12】例题7(回文串那题)的N变成5000,其余不变。
回忆一下那个问题的状态转移方程如下:
d[i][j] = {
d[i+1][j-1] | A[i] == A[j]
min{ d[i+1][j], d[i][j-1] } + 1 | A[i] != A[j]
}
我们发现将d[i][j]理解成一个二维的矩阵,i表示行,j表示列,那么第i行的结果只取决于第i+1和第i行的情况,对于第i+2行它表示并不关心,那么我们只要用一个d[2][N]的数组就能保存状态了,其中d[0][N]为奇数行的状态值,d[1][N]为偶数行的状态值,当前需要计算的状态行数为奇数时,会利用到d[1][N]的部分状态,奇数行计算完毕,d[1][N]整行状态都没用了,可以用于下一行状态的保存,类似“传送带”的滚动来循环利用空间资源,美其名曰 – 滚动数组。
这是个2D/0D问题,理论的空间复杂度是O(n2),利用滚动数组可以将空间降掉一维,变成O(n)。
背包问题的几个状态转移方程同样可以用滚动数组进行空间优化。
2、最长单调子序列
d[i] = max{ d[j] | j < i && a[j] < a[i] } + 1;
那个问题的状态转移方程如下:
【例题13】例题4(最长递增子序列那题)的N变成100000,其余不变。
首先明确决策的概念,我们认为 j 和 k (j < i, k < i)都是在计算d[i]时的两个决策。那么假设他们满足a[j] < a[k](它们的状态对应就是d[j] 和 d[k]),如果a[i] > a[k],则必然有a[i] > a[j],能够选k做决策的也必然能够选 j 做决策,那么如若此时d[j] >= d[k],显然k不可能是最优决策(j的决策始终比它优,以j做决策,a[ j ]的值小但状态值却更大),所以d[k]是不需要保存的。
基于以上理论,我们可以采用二分枚举,维护一个值 (这里的值指的是a[i]) 递增的决策序列,不断扩大决策序列,最后决策的数目就是最长递增子序列的长度。具体做法是:枚举i,如果a[i]比决策序列中最大的元素的值还大,则将i插入到决策序列的尾部;否则二分枚举决策序列,找出其中值最小的一个决策k,并且满足a[k] > a[i],然后用决策i替换决策k。
这是个1D/1D问题,理论的时间复杂度是O(n2),利用单调性优化后可以将复杂度将至O(nlogn)。
【例题14】
给定n个元素(n <= 100000)的序列,将序列的所有数分成x堆,每堆都是单调不增的,求x的最小值。
结论:可以转化成求原序列的最长递增子序列。
证明:因为这x堆中每堆元素都是单调不增的,所以原序列的最长递增子序列的每个元素在分出来的每堆元素中一定只出现最多一个,那么最长递增子序列的长度L的最大值为x,所以x >= L。
而我们要求的是x的最小值,于是这个最小值就是 L 了。
3、矩阵优化
【例题15】三个小岛,编号1、2、3,老王第0天在1号岛上。这些岛有一些奇怪的规则,每过1天,1号岛上的人必须进入2、3号岛;2号岛上的人必须进入1号岛;3号岛上的人可以前往1、2或留在3号岛。问第n(n <=109)天老王在到达1号岛的行走方案,由于数据比较大,只需要输出 ans MOD 100000007的值即可。
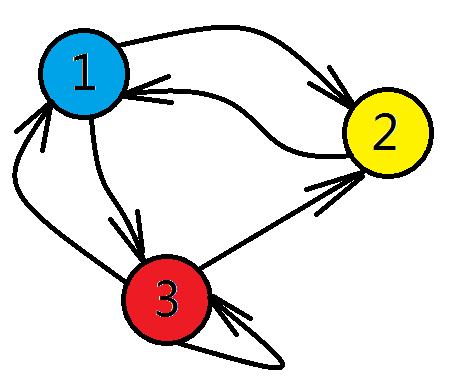
图四-3-1
临时想的一个问题,首先看问题有几个维度,岛和天数,而且状态转移是常数级的,所以这是个2D/0D问题,我们用f[i][j]表示第i天在j号岛上的方案数,那么初始状态f[0][1] = 1, f[0][2] = f[0][3] = 0。
状态转移可以参考图四-3-1,有:
f[i][1] = f[i-1][2] + f[i-1][3]
f[i][2] = f[i-1][1] + f[i-1][3]
f[i][3] = f[i-1][1] + f[i-1][3]
我们要求的结果就是f[n][1],再来看n的范围比较大,虽然是几个简单的加法方程,但是一眼看下去也不知道有什么规律可循。我们把状态转移用另外一种形式表现出来,存储图的连通信息的一种方法就是矩阵,如图四-3-2
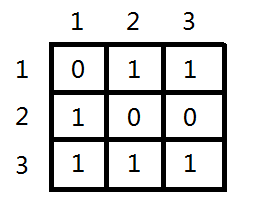
图四-3-2
令这个矩阵为A,Aij表示从i号岛到j号岛是否连通,连通标1,不连通标0,它还有另外一个含义,就是经过1天,从i岛到j岛的方案数,利用矩阵的传递性,A2的第i行的第j列则表示经过2天,从i岛到j岛的方案数,同样的,An 则表示了经过n天,从i岛到j岛的方案数,那么问题就转化成了求AnMOD 100000007的值了。An当n为偶数的时候等于(An/2)*(An/2);当n为奇数的时候,等于(An/2)*(An/2)*A,这样求解矩阵An就可以在O(logn)的时间内完成了,加法和乘法对MOD操作都是可交换的(即 “先加再模” 和 “先模再加再模” 等价),所以可以在矩阵乘法求解的时候,一旦超出模数,就执行取模操作。
最后求得的矩阵T = An MOD100000007,那么T[1][1]就是我们要求的解了。
4、斜率优化
【例题16】n(n <= 500000)个单词,每个单词输出的花费为Ci(1 <= i <= n),将k个连续的单词输出在一行的花费为:
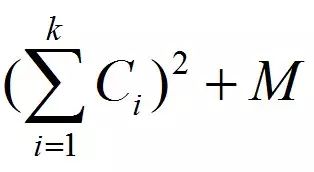
其中M为常数,求一个最佳方案,使得输出所有单词总的花费最小。令d[i]为前i个单词组织出的最小花费,s[i] = sum{Ck | 0 <= k <= i },其中s[0] = 0
状态转移方程 d[i] = min{ d[j] + (s[i] – s[j])2 + M | 0 <= j < i } (1 <= i <= n)这是个1D/1D问题,空间复杂度O(n), 时间复杂度为O(n2),对于500000的数据来说是不可能在给定时间出解的。
令g[j] = d[j] + (s[i] – s[j])2+ M,表示由 j 到 i 的决策。对于两个决策点 j < k,如果k的决策值小于j (即g[k] < g[j]),则有:d[k] + (s[i] – s[k])2+ M < d[j] + (s[i] – s[j])2+ M,然后将左边转化成关于j和k的表达式,右边转化成只有i的表达式。 (中间省略t行推导过程…,t >= 5)
(d[j] – d[k] + s[j]2- s[k]2) / (s[j] – s[k]) < 2*s[i]
令xj = d[j] + s[j]2, yj = s[j],则原式转化成: (xj – xk) / (yj – yk) < 2*s[i]
不等式左边是个斜率的形式,我们用斜率函数来表示 slope(j, k) = (xj – xk) / (yj – yk),那么这里我们可以得出两个结论:
当两个决策j、k (j < k)满足 slope(j, k) < 2*s[i]时,j决策是个无用决策,并且因为s[i]是个单调不降的,所以对于i < i’,则有slope(j, k) < 2*s[i] < 2*s[i'],即j决策在随着i增大的过程中也是一直都用不到的。
对于当前需要计算的值f[i],存在三个决策j、k、l,并且有 j < k < l,如果slope(j, k) > slope(k, l),则k这个决策是个无用决策,证明需要分情况讨论:
slope(k, l) < 2*s[i],则l的决策比k更优;
slope(k, l) >= 2*s[i],则 slope(j, k) > slope(k, l) >= 2*s[i],j的决策比k更优;
综上所述,当slope(j, k) > slope(k, l)时,k是无用决策;那么可以用单调队列来维护一个决策队列的单调性,单调队列存的是决策序列。一开始队列里只有一个决策,就是0这个点(虚拟出的初始决策),根据第一个结论,如果队列里面决策数目大于1,则判断slope( Q[front], Q[front+1] ) < 2*s[i]是否成立,如果成立,Q[front]是个无用决策,front ++,如果不成立那么Q[front]必定是当前i的最优决策,通过状态转移方程计算f[i]的值,然后再根据第二个结论,判断slope(Q[rear-2], Q[rear-1]) > slope(Q[rear-1], i)是否成立,如果成立,那么Q[rear-1]必定是个无用决策,rear –,如果不成立,则将 i 作为当前决策 插入到队列尾, 即 Q[rear++] = i。
这题需要注意,斜率计算的时候,分母有可能为0的情况。
5、树状数组优化
树状数组是一种数据结构,它支持两种操作:
对点更新,即在给你(x, v)的情况下,在下标x的位置累加一个和v(耗时 O(log(n)) )。
函数表示 void add(x, v);
成端求和,给定一段区间[x, y],求区间内数据的和(这些数据就是第一个操作累加的数据,耗时O(log(n)))。
函数表示 int sum(x, y);
用其它数据结构也是可以实现上述操作的,例如线段树(可以认为它是一种轻量级的线段树,但是线段树能解决的问题更加普遍,而树状数组只能处理求和问题),但是树状数组的实现方便、常数复杂度低,使得它在解决对点更新成端求和问题上成为首选。这里并不会讲它的具体实现,有兴趣请参见树状数组。
【例题17】给定一个n(n <= 100000)个元素的序列a[i] (1 <= a[i] <= INF),定义”和谐序列”为序列的任何两个相邻元素相差不超过K,求a[i]的子序列中,”和谐序列”的个数 MOD 10000007。用d[i]表示以第i个元素结尾的”和谐序列”的个数, 令d[0] = 1, 那么sum {d[i] | 1 <= i <= n}就是我们要求的解。列出状态转移方程:
d[i] = sum{ d[j] | j==0 || j < i && abs(a[i] – a[j]) <= K }
这是一个1D/1D问题,如果不进行任何优化,时间复杂度是O(n^2)。我们首先假设K是个无限大的数,也就是不考虑abs(a[i] – a[j]) <= K这个限制,那这个问题要怎么做?很显然d[1] = 1,d[2] = 1 + d[1],d[3] = d[1] + d[2] + 1(这里的1其实是状态转移方程中j == 0的情况,也就是只有一个数a[i]的情况),更加一般地:
d[i] = sum{d[j] | j < i} + 1
对于这一步状态转移还是O(n)的,但是我们可以将它稍加变形,如下:
d[i] = sum(1, INF) + 1; (这里的sum是树状数组的区间求和函数)得到d[i]的值后,再将d[i]插入到树状数组中,利用树状数组第1条操作 add(a[i], d[i]);
基于这样的一种思路,我们发现即使有了限制K,同样也是可以求解的,只是在求和的时候进行如下操作:
d[i] = sum(a[i] – K, a[i] + K) + 1;
这样就把原本O(n)的状态转移变成了 O(logn),整个算法时间复杂度O(logn)。
6、线段树优化
是一种完全二叉树,它支持区间求和、区间最值等一系列区间问题,这里为了将问题简化,直接给出求值函数而暂时不去讨论它的具体实现,有兴趣的可以自行寻找资料。线段树可以扩展到二维,二维线段树是一棵四叉树,一般用于解决平面统计问题,参见二维线段树
这里给出线段树的求区间最值需要用到的函数,即:
insert(x, v) 在下标为x的位置插入一个值v; 耗时 O( log(n) )
query(l, r) 求下标在[l, r]上的最值; 耗时 O( log(n) )
【例题18】详见 例题13
还是以最长单调子序列为例,状态转移方程为:
d[i] = max{ d[j] | j < i && a[j] < a[i] } + 1
这里我们首先要保证 1 <= a[i] <= n,如果a[i]是实数域的话,首先要对a[i]进行离散化,排序后从小到大重新编号,最小的a[i]编号为1,最大的a[i]编号为n。
对于状态转移执行线段树的询问操作: d[i] = query( 1, a[i] – 1 ) + 1
然后再执行插入操作: insert( a[i], d[i] )
状态转移同样耗时O(logn)。
这个思想和树状数组的思想很像,大体思路都是将数本身映射到某个数据结构的下标。
7、其他优化
散列HASH状态表示
结合数论优化
结合计算几何优化
四边形不等式优化
等等
五、动态规划题集整理
1、递推
Recursion Practice ★☆☆☆☆ 几个初级递推
Put Apple ★☆☆☆☆
Tri Tiling ★☆☆☆☆ 【例题1】
Computer Transformation ★☆☆☆☆ 【例题2】
Train Problem II ★☆☆☆☆
How Many Trees? ★☆☆☆☆
Buy the Ticket ★☆☆☆☆
Game of Connections ★☆☆☆☆
Count the Trees ★☆☆☆☆
Circle ★☆☆☆☆
Combinations, Once Again ★★☆☆☆
Closing Ceremony of Sunny Cup ★★☆☆☆
Rooted Trees Problem ★★☆☆☆
Water Treatment Plants ★★☆☆☆
One Person ★★☆☆☆
Relax! It’s just a game ★★☆☆☆
N Knight ★★★☆☆
Connected Graph ★★★★★ 楼天城“男人八题”之一
2、记忆化搜索
Function Run Fun ★☆☆☆☆ 【例题3】
FatMouse and Cheese ★☆☆☆☆ 经典迷宫问题
Cheapest Palindrome ★★☆☆☆
A Mini Locomotive ★★☆☆☆
Millenium Leapcow ★★☆☆☆
Brackets Sequence ★★★☆☆ 经典记忆化
Chessboard Cutting ★★★☆☆ 《算法艺术和信息学竞赛》例题
Number Cutting Game ★★★☆☆
3、最长单调子序列
Constructing Roads In JG Kingdom★★☆☆☆
Stock Exchange ★★☆☆☆
Wooden Sticks ★★☆☆☆
Bridging signals ★★☆☆☆
BUY LOW, BUY LOWER ★★☆☆☆ 要求需要输出方案数
Longest Ordered Subsequence ★★☆☆☆
Crossed Matchings ★★☆☆☆
Jack’s struggle ★★★☆☆ 稍微做点转化
4、最大M子段和
Max Sum ★☆☆☆☆ 最大子段和
Max Sum Plus Plus ★★☆☆☆ 最大M子段和
To The Max ★★☆☆☆ 最大子矩阵
Max Sequence ★★☆☆☆ 最大2子段和
Maximum sum ★★☆☆☆ 最大2子段和
最大连续子序列 ★★☆☆☆ 最大子段和
Largest Rectangle in a Histogram ★★☆☆☆ 最大子矩阵变形
City Game ★★☆☆☆ 最大子矩阵扩展
Matrix Swapping II ★★★☆☆ 最大子矩阵变形后扩展
5、线性模型
Skiing ★☆☆☆☆
Super Jumping! Jumping! Jumping! ★☆☆☆☆
Milking Time ★★☆☆☆ 区间问题的线性模型
Computers ★★☆☆☆ 【例题5】
Bridge over a rough river ★★★☆☆ 【例题6】
Crossing River ★★★☆☆ 【例题6】大数据版
Blocks ★★★☆☆
Parallel Expectations ★★★★☆ 线性模型黑书案例
6、区间模型
Palindrome ★☆☆☆☆ 【例题7】
See Palindrome Again ★★★☆☆
7、背包模型
饭卡 ★☆☆☆☆ 01背包
I NEED A OFFER! ★☆☆☆☆ 概率转化
Bone Collector ★☆☆☆☆ 01背包
最大报销额 ★☆☆☆☆ 01背包
Duty Free Shop ★★☆☆☆ 01背包
Robberies ★★☆☆☆ 【例题8】
Piggy-Bank ★☆☆☆☆ 完全背包
Cash Machine ★☆☆☆☆ 多重背包
Coins ★★☆☆☆ 多重背包,楼天城“男人八题”之一
I love sneakers! ★★★☆☆ 背包变形
8、状态压缩模型
ChessboardProblem ★☆☆☆☆ 比较基础的状态压缩
Number of Locks ★☆☆☆☆ 简单状态压缩问题
Islands and Bridges ★★☆☆☆ 【例题9】
Tiling a Grid With Dominoes ★★☆☆☆ 骨牌铺方格 4XN的情况
Mondriaan’s Dream ★★☆☆☆ 【例题10】的简易版
Renovation Problem ★★☆☆☆ 简单摆放问题
The Number of set ★★☆☆☆
Hardwood floor ★★★☆☆ 【例题10】二进制状态压缩鼻祖
Tetris Comes Back ★★★☆☆ 纸老虎题
Bugs Integrated, Inc. ★★★☆☆ 三进制状态压缩鼻祖
Another Chocolate Maniac ★★★☆☆ 三进制
Emplacement ★★★☆☆ 类似Bugs那题,三进制
Toy bricks ★★★☆☆ 四进制, 左移运算高于&
Quad Tiling ★★★☆☆ 骨牌铺方格 4XN的情况 利用矩阵优化
Eat the Trees ★★★☆☆ 插头DP入门题
Formula 1 ★★★☆☆ 插头DP入门题
The Hive II ★★★☆☆ 插头DP
Plan ★★★☆☆ 插头DP
Manhattan Wiring ★★★☆☆ 插头DP
Pandora adventure ★★★★☆ 插头DP
Tony’s Tour ★★★★☆ 插头DP,楼天城“男人八题”之一
Pipes ★★★★☆ 插头DP
circuits ★★★★☆ 插头DP
Beautiful Meadow ★★★★☆ 插头DP
I-country ★★★★☆ 高维状态表示
Permutaion ★★★★☆ 牛逼的状态表示
01-K Code ★★★★☆
Tour in the Castle ★★★★★ 插头DP(难)
The Floor Bricks ★★★★★ 四进制(需要优化)
9、树状模型
Anniversary party ★☆☆☆☆ 树形DP入门
Strategic game ★☆☆☆☆ 树形DP入门
Computer ★★☆☆☆
Long Live the Queen ★★☆☆☆
最优连通子集 ★★☆☆☆
Computer Network ★★☆☆☆
Rebuilding Roads ★★★☆☆ 树形DP+背包
New Year Bonus Grant ★★★☆☆
How Many Paths Are There ★★★☆☆
Intermediate Rounds for Multicast ★★★★☆
Fire ★★★★☆
Walking Race ★★★★☆
Tree ★★★★★ 树形DP,楼天城“男人八题”之一
10、滚动数组优化常见问题
Palindrome ★☆☆☆☆
Telephone Wire ★☆☆☆☆
Gangsters ★☆☆☆☆
Dominoes ★☆☆☆☆
Cow Exhibition ★☆☆☆☆
Supermarket ★★☆☆☆
11、决策单调性
Print Article ★★★☆☆
Lawrence ★★★☆☆
Batch Scheduling ★★★☆☆
K-Anonymous Sequence ★★★☆☆
Cut the Sequence ★★★☆☆
12、常用优化
Divisibility ★★☆☆☆ 利用同余性质
Magic Multiplying Machine ★★☆☆☆ 利用同余性质
Moving Computer ★★☆☆☆ 散列HASH表示状态
Post Office ★★★☆☆ 四边形不等式
Minimizing maximizer ★★★☆☆ 线段树优化
Man Down ★★★☆☆ 线段树优化
So you want to be a 2n-aire? ★★★☆☆ 期望问题
Expected Allowance ★★★☆☆ 期望问题
Greatest Common Increase Subseq ★★★☆☆ 二维线段树优化
Traversal ★★★☆☆ 树状数组优化
Find the nondecreasing subsequences ★★★☆☆ 树状数组优化
Not Too Convex Hull ★★★★☆ 利用凸包进行状态转移
In Action ★★★☆☆ 最短路+背包
Search of Concatenated Strings ★★★☆☆ STL bitset 应用
13、其他类型的动态规划
Common Subsequence 2D/0D
Advanced Fruits 2D/0D
Travel 2D/1D
RIPOFF 2D/1D
Balls 2D/1D
Projects 2D/1D
Cow Roller Coaster 2D/1D
LITTLE SHOP OF FLOWERS 2D/1D
Pearls 2D/1D
Spiderman 2D/0D
The Triangle 2D/0D
Triangles 2D/0D
Magazine Delivery 3D/0D
Tourist 3D/0D
Rectangle 2D/1D
Message 2D/1D
Bigger is Better 2D/1D
Girl Friend II 2D/1D
Phalanx 2D/1D
Spiderman 最坏复杂度O(NK),K最大为1000000,呵呵
Find a path 3D/1D 公式简化,N维不能解决的问题试着用N+1维来求解
觉得本文有帮助?请分享给更多人
关注「算法爱好者」,修炼编程内功
















