专栏名称: COMSOL 多物理场仿真技术
| 致力于介绍COMSOL多物理场仿真技术,涉及声-结构、MEMS、数学等模块,教学sci文献案例,讲解仿真要点以及定期分享最新的声学超材料文献 |
目录
相关文章推荐
51好读
›
专栏
›
COMSOL 多物理场仿真技术
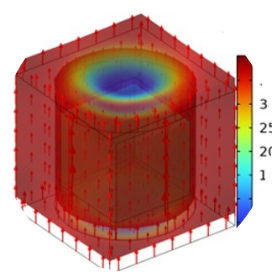
学术前沿 | 湍流激励空腔-板-外部空间耦合系统的振动声学建模
COMSOL 多物理场仿真技术 · 公众号 · · 2024-08-15 21:50
推荐文章

|
青年文摘 · 思考:手机到底拿走了你的什么? 8 年前 |

|
教育百师通 · 管多了怕懦弱,管少了怕养成坏习惯!孩子到底怎么管? 8 年前 |

|
老子道德经 · 致:傻傻的自己 (看了好心酸) 8 年前 |

|
精英点评江西 · 潮玩 | 摸姐嘲笑你是一个没有任何瘾的人 7 年前 |

|
上海译文 · 吉卜力在招聘,你敢去投奔“宁愿在工作中死去的男人”宫崎骏吗? 7 年前 |