2.1 Hull-White 模型
模型介绍
利率类的 Hull-White (HW) 模型下的 SDE 是描述短期利率 (short rate) 的走势:
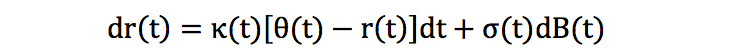
其中
r(t) = 短期利率
k( )=r(t)的均值回归速率
ς( )=r(t)的均值
6(t)= r(t)的波动率
B(t) = 布朗运动
该模型是 John Hull 和 Alan White 在 1990 年提出,其论文题目是
Pricing Interest-Rate Derivative Securities
模型参数
一般情况下
k (t) 当成常数
6(t) 可以是常数,但通常是分段常数
ς(t )是 t 的函数
它们的获取方式为
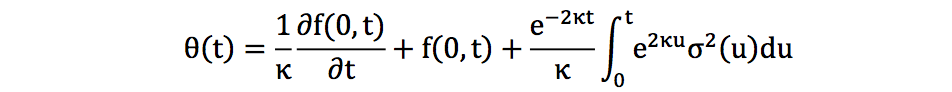
其中 f(0, t)是 0 点观察到的 t 点瞬时远期利率
为了消除 ( ) 这个复杂项,令 x(t) = r(t) – f(0, t),那么 x(0) = r(0) –f(0,0) = 0。原来 r(t) 的 SDE 转换成 x(t) 的 SDE:
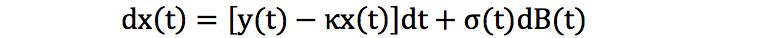
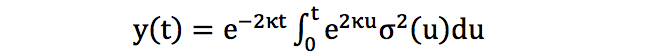
这样在 HW 模型下的零息债券的公式如下:
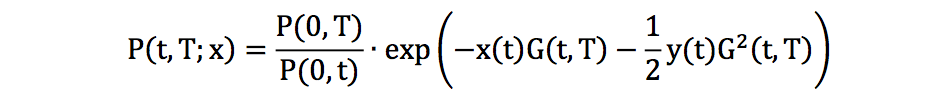

关于上面 ( ) 和 P(t, T) 推导细节,可以参考 Interest Rate Modeling Volumn II, Term Structure Model, Chapter 10, 10.1.2.2.
2.2 市场标准产品和数据
产品定义
利率类市场标准产品包括:
1. 一系列不同行权价格 K 和不同年限 T 利率上限 (cap)
2. 一系列不同行权价格 K,不同期权年限 TO 和不同掉期年限 TU 利率
掉期期权 (swaption) Cap 和 swaption 定义如下:
Cap 和 swaption 定义如下:
在利率上限或下限 (interest rate cap/floor) 合约下,买方和卖方将同意以 下内容:
买方付出期权金 (premium) 便有权利 (right) 去行使,而卖方收取期权金后则有义务 (obligation) 履行买方行使权利的义务。
双方就未来某一时期商定一个固定利率 K 作为利率上限/下限
上限:买方有权利在每期获得市场利率 L 与上限利率 K 的差额 (L – K),而卖方一旦被行使期权时,则有义务将市场利率 L 与上限利率 K 的差额支付给买方
下限:买方有权利在每期获得下限利率 K 和市场利率 L 的差额 (K – L),而卖方一旦被行使期权时,则有义务将下限利率 K 和市场利率 L 的差额支付给买方
其中 L 通常是 LIBOR,但是不是当期定盘,而是上一期定盘的 LIBOR。
市场上流动性强的 cap 以美元、欧元和日元计价,每个 cap 都一连串 caplet 组成
USD cap 每年由 4 个 caplet 组成,每个 caplet 期限是 3 个月,以 USD LIBOR 3M 作标的利率
EUR cap 每年由 2 个 caplet 组成,每个 caplet 期限是 6 个月,以 EUR EURIBOR 6M 作标的利率
JPY cap 每年由 2 个 caplet 组成,每个 caplet 期限是 6 个月,以 JPY LIBOR 6M 作标的利率
在利率掉期期权 (interest rate swaption) 合约下,买方和卖方将同意以下 内容:
买方付出期权金 (premium) 便有权利 (right) 去行使,而卖方收取 期权金后则有义务 (obligation) 履行买方行使权利的义务。
支付类掉期期权 (payer swaption):买方有权利在期权到期日获得 一个“支付固定利率接受浮动利率 (pay fixed receive floating) 的利率 掉期”,而卖方一旦被行使期权时,则有义务将上述利率掉期给买 方
接受类掉期期权 (payer swaption):买方有权利在期权到期日获得一个“接受固定利率支付浮动利率 (receive fixed pay floating) 的利率 掉期”,而卖方一旦被行使期权时,则有义务将上述利率掉期给买 方
其中利率掉期 (interest rate swap, IRS) 是指交易双方以一定的名义本金为 基础,将该本金产生的一种利率计算的利息收入 (支出) 与另一种利率计 算的利息收入 (支出)。交换的只是不同特征的利息,没有实质本金的互 换。
市场上流动性强的以美元、欧元和日元计价的 swaption。其实 swaption 波动率是一个立方 (cube),有行权利率、期权到期日、掉期到期日这三 个维度。通常我们用的最多的是 ATM swaption 波动率,当行权利率等于 远期掉期率,那么波动率立方降维成一个波动率平面,维度为二维。
市场数据
某天的 JPY cap 的真实数据如下:
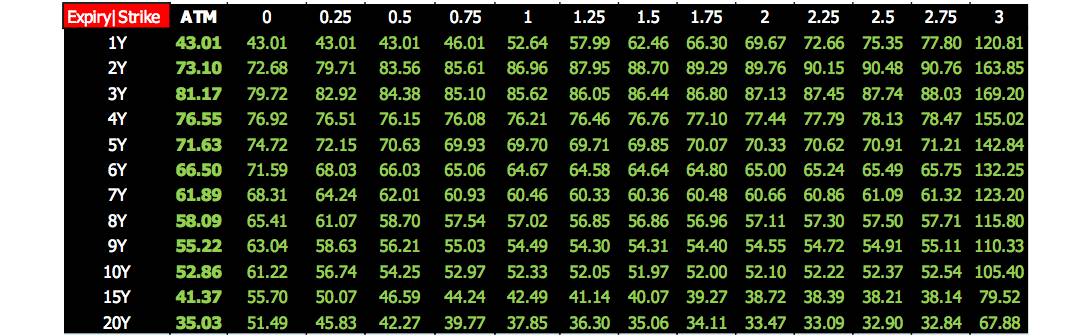
上图数据又称 cap 波动率平面,它是二维数据结构
行对应的年限 (expiry),期权年限从 1 年到 20 年
列对应的行权利率 (strike rate),注意第一列绿色粗体是 ATM 波动率,而每个年限对应的 ATM 行权利率都不同
波动率与行权价格和年限有关,可写成 ς(K, T)
波动率单位是 %,43.01 实际上指的是 43.01%
市场波动率带进 Black 公式得到利率上限的市场价格
某天的 USD ATM swaption 的真实数据如下:
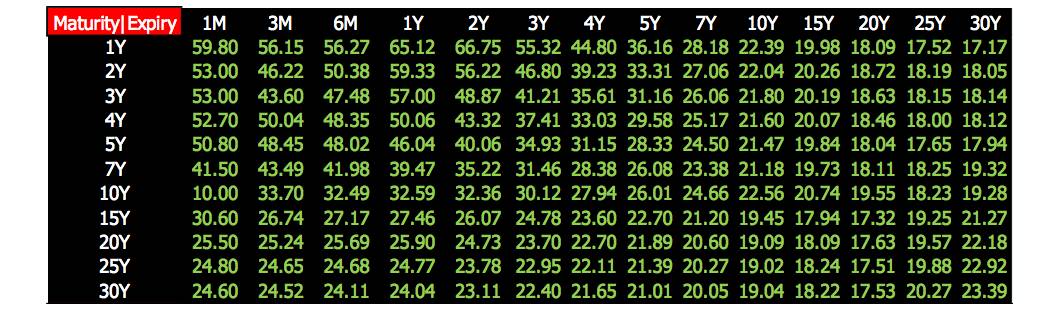
上图数据又称 ATM swaption 波动率平面,它是二维数据结构
行对应的利率掉期的年限 (maturity),年限从 1 年到 30 年
列对应的掉期期权的年限 (expiry),年限从 1 个月到 30 年
ATM 波动率与期权年限和掉期年限有关,可写成 ς(TO, TU)
波动率单位是%,59.80 实际上指的是 59.80%
市场波动率带进 Black 公式得到掉期期权的市场价格
2.3 市场价格和模型价格
定义T0
{T0, T1, ..., TN-1} = LIBOR 定盘日
{T1, T2, ..., TN} = 支付日
N = caplet 的个数
τk =Tk–Tk-1
Cap 市场价格
Cap 市场价格是之后模型校正的基准 (benchmark)。关于 Black 模型的 cap 推导细节,可以参考 Interest Rate Model – Theory and Practice, Chapter 1 and Appendix D.

Cap 模型价格

当模型参数为常数时,关于 HW 模型的 cap 推导细节,可以参考 Interest Rate Model – Theory and Practice, Chapter 3.
function price = HW_IRO( omega, Ds, De, Ts, Te, tau, K, kappa, sigma )
X = 1 + K*tau;
price = X .* HW_ZBO( -omega, Ts, Te, Ds, De, 1./X, kappa, sigma );
end
--------------------------------------
function price = HW_ZBO( omega, T1, T2, PT1, PT2, X, kappa, sigma )
tau = T2 - T1;
if kappa < 1e-12
sigmaP = sigma * tau .* sqrt(T1);
else
sigmaP = sigma * sqrt((1-exp(-2*kappa*T1))/2/kappa) /kappa .* (1- exp(-kappa*tau));
end
h1 = (1./sigmaP) .* log(PT2./(PT1.*X)) + sigmaP/2;
h2 = h1 - sigmaPprice = omega * ( PT2.*normcdf(omega*h1) - X.*PT1.*normcdf(omega*h2) )
end

Swaption 市场价格
定义T0
T0 = swaption 到期日
TN = swap 到期日
τk =Tk–Tk-1

Swaption 市场价格是之后模型校正的基准 (benchmark)。关于 Black 模 型的 Swaption 推导细节,可以参考 Interest Rate Model – Theory and Practice, Chapter 1 and Appendix D.
Swaption 模型价格
Swaption 可看成在期权到期日 T1 时交换 IRS 的固定端和浮动端,因此它在 T1 的支付函数为
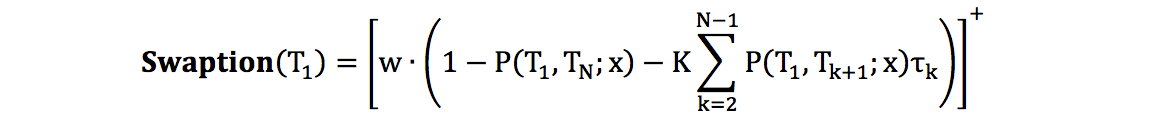
由小节 2.1 可知 P(t, T;x)是 x 的减函数,因此定义一个临界值 x* 使得
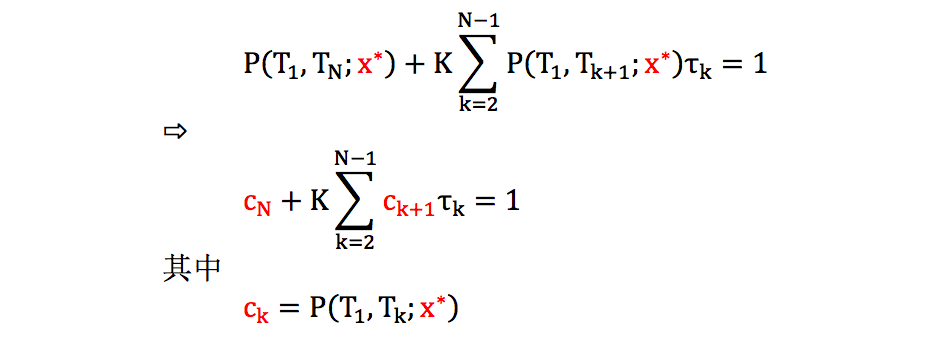
其中
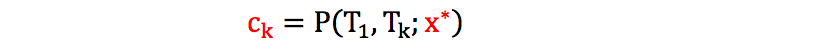
根据 Jamshidian Trick,swaption 只有在 w x(T1) > * 时才有 payout, 为了简化符号引进 P1,k(x) = P(T1,Tk, x),我们有
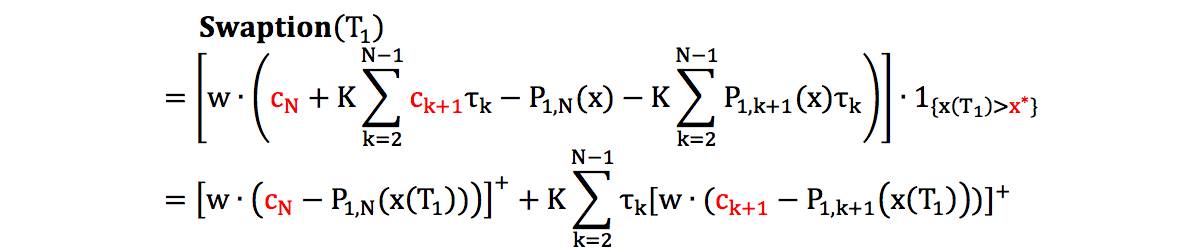
最后 swaption 在 T1 的 payout 可表示为一系列的零息债券期权 (zero- coupon bond option, ZBO) 在的 payout,因此其价值为这些 ZBO 的价值 的组合。

function price = HW_Swaption( D, Tvec, tau, c, kappa, sigma )
Pt = D(1); PT = D(2:end); t = Tvec(1); T = Tvec(2:end);
x_star = fzero( @(x) Jamshidian( Pt, PT, kappa, sigma, t, T, c, tau, x ), 0 );
K = HW_zcb( Pt, PT, kappa, sigma, t, T, x_star )';
price = HW_ZBO( -1, t, T(end), Pt, PT(end), K(end), kappa, sigma ) ... + c*sum( tau.*HW_ZBO( -1, t, T, Pt, PT, K, kappa, sigma ) );
end
function y = Jamshidian( Pt, PT, kappa, sigma, t, T, c, tau, x )
y = HW_zcb(Pt, PT(end), kappa, sigma, t, T(end), x) ...
+ c*sum( tau.*HW_zcb(Pt, PT, kappa, sigma, t, T, x)' ) - 1;
end
--------------------------------------
function PtT = HW_zcb( Pt, PT, kappa, sigma, t, T, Xt )
G = 1-exp(-kappa*(T-t))) / kappa;
y = sigma^2 * (1-exp(-2*kappa*t)) / (2*kappa)
PtT = (PT/Pt) * exp( -Xt*G -0.5*y*G^2 );
end

关于 HW 模型的 swaption 推导细节,可以参考 Interest Rate Modeling – Volumn II, Term Structure Model, Chapter 10, 10.1.3.
2.4 模型校正 (cap)
在 cap 市场上,对每一个标准 K 有 n 个到期的 cap,到期日分别为
0 = T0 < T1 < ... < i < ... < n
而对于每一个 Ti,cap 的行权价格为 K1 ... j ... m。 接下来我们分别讨论当模型参数为常数和分段常数是的校正过程。
常数型参数
当参数为常数时,HW 模型校正本质上是找到“最优” 和 ς,从而最小 化一系列 cap 的市场价格和模型价格之间的差异,其目标函数为:

其中
分段常数型参数
从小节 2.3 的公式出发,

当参数为分段常数时,假设选取 ATM cap 做校正,那么 HW 模型校正的 步骤为:
步骤 1 - 参数 根据历史数据手动输入,或者用常数形式的 HW 模型校 正得出
步骤 2 - 对第 1 个 cap,反解 ς1 使得 Capmkt(T1) = Cap1HW(ς1)
步骤 3 - 对第 2 个 cap,已知 ς1,反解 ς2 使得 Capmkt(T2) = Cap2HW(ς1,ς2)
步骤 4 - 重复上面过程到第 n 个 cap,已知 ς1, ς2 ... ςn-1,反解 ςn 使得 Capmkt(Tn) = CapnHW(ς1,ς2 ... ςn-1,ςn)
sigma = zeros(num_of_T,1);
for i = 1 : num_of_T,
[ itau, iTs, iTe, iDs, iDe ] = reference( (1:nFlt(i)-1), tau, Ts, Te, Ds, De );
sigma(i) = fzero(@(x) Cap_diff( iDs, iDe, iTs, iTe, itau, K(i), kappa, x, mkt_price(i) ), 0.005 );
end
以上过程把 1 个 n 维的优化问题转成 n 个 1 维的优化问题,增加了模型 校正的效率。需要注意的是,上述步骤并不是每次都行得通,这种情况称 为“波动率紧缩 (volatility squeeze)”,出现在当 Ti+1 到期的 cap 比 Ti 到期的 cap 价格小很多的时候。这种情况很少见,一旦出现可以当成是套 利的信号。
2.5 模型校正 (swaption)
在 ATM swaption 市场上,在以下的年限结构上考虑一串特殊的 swaption
0 = T0 < T1 < ... < i < ... < n
此类 swaption 的 option 到期日为 Ti, ... -1,而它们的 swap 到 期日都是 Tn,这样的 swaption 成为 coterminal swaption,记作 aYbY, 指的是 a 年 option 到期可以换一个 b 年 swap 的 swaption。
由于此类结构和市场交易的百慕大期权 (Bermudan swaption) 很类似,因 此 coterminal swaption 经常被当作校正工具来使用。
接下来我们分别讨论当模型参数为常数和分段常数是的校正过程。
常数型参数
当参数为常数时,HW 模型校正本质上是找到“最优” 和 ς,从而最小 化一系列 coterminal swaption 的市场价格和模型价格之间的差异,其目 标函数为:
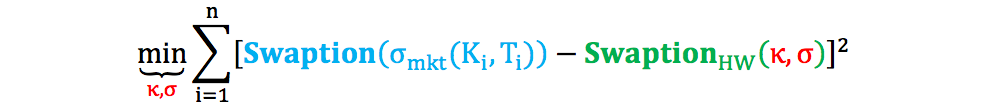
其中
分段常数型参数

当参数为分段常数时,选取 ATM coterminal swaption 做校正,那么 HW 模型校正的步骤为:
步骤 1 - 参数 根据历史数据手动输入,或者用常数形式的 HW 模型校 正而得
步骤 2 - 对第 1 个 swaption,反解 ς1 使得 swaptionmkt(T1) = swaption1HW(ς1)
步骤 3 - 对第 2 个 swaption,已知 ς1,反解 ς2 使得 swaptionmkt(T2) = swaption2HW(ς1,ς2)
步骤 4 - 重复上面过程到第 n-1 个 swaption,已知 ς1, ς2 ... ςn-2,反解 ςn- 1 使得 swaptionmkt(Tn-1) = swaptionn-1HW(ς1,ς2 ... ςn-2,ςn-1)
sigma = zeros(num_of_T,1);
for i = 1 : num_of_T,
T = getTenor( settle, fixedLegDate{i}, 'act/365' );
D = getDiscount( settle, spotDate, fixedLegDate{i}, LiborCurve );
[ iT, iD ] = reference( 1:nFix(i), T, D );
sigma(i) = fzero(@(x) Swaption_diff( iD, iT, fixtau{i,i}, K(i),
kappa, x, mkt_price(i) ), 0.005 );
end
和 cap 校正是遇到的问题一样,波动率紧缩也是 swaption 的校正可能出 现的问题。该情况出现在当 Ti+1 到期的 swaption 比 Ti 到期的 swaption 价格小很多的时候。这种情况很少见,一旦出现可以当成是套利的信号。
2.6 校正结果
下图展示着当 和 ς 为常数时,USD ATM cap 的市场价格 (红圈) 和模型 价格 (蓝线),发现它们在不同 T 时结果相近但不完全吻合,原因是 2 个 未知量来拟合 13 个 cap,只能平均接近不能各个匹配。
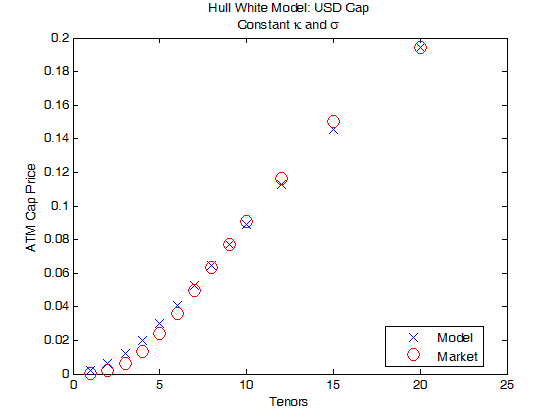
下图展示着当 为已设好的 0.01 和 ς(t) 为分段常数时,USD ATM cap 的 市场价格 (红圈) 和模型价格 (蓝线),发现它们在不同 T 时完全吻合,原 因是当 已知,每个 cap 和 ς 是一一对应关系。
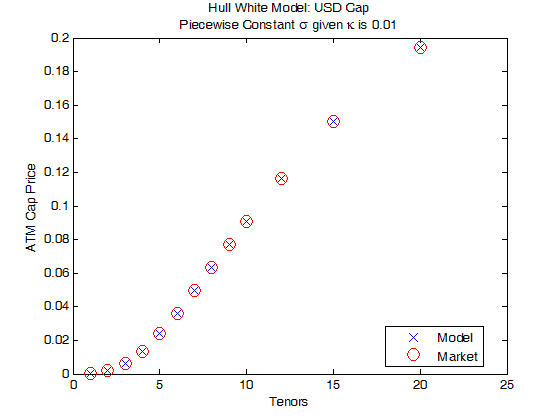
下图展示着当 和 ς 为常数时,USD ATM coterminal swaption 的市场价 格 (红圈) 和模型价格 (蓝线),发现它们在短期 T 时结果相近但长期 T 相 差很远。原因是 2 个未知量来拟合 11 个 cap,只能平均接近不能各个匹 配,而且后面几个 swaption 的到期日从 15 年到 30 年,常数参数很难能 把这么长的掉期期权拟合好。
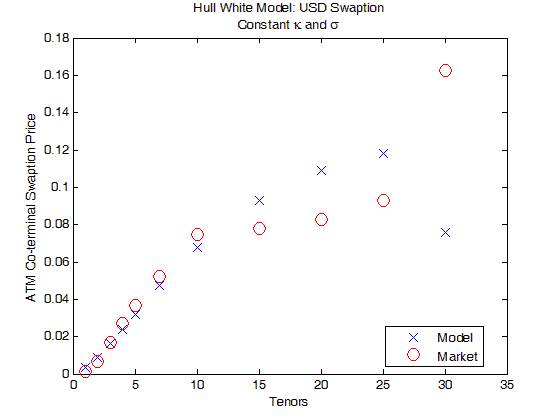
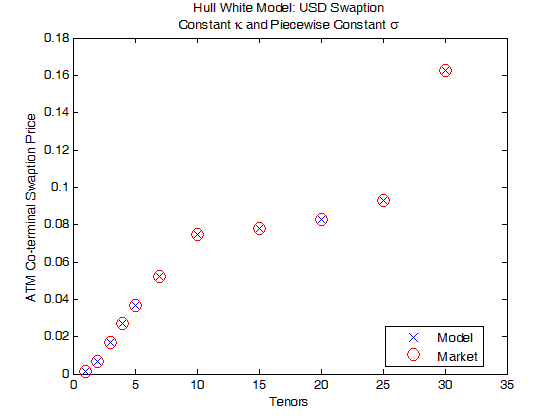
下图展示着当 为常数和 ς( ) 为分段常数时,USD ATM coterminal swaption 的市场价格 (红圈) 和模型价格 (蓝线),发现它们在不同 T 时完 全吻合,原因是当 先校正好,每个 swaption 和 ς 是一一对应关系。