来自:Matrix67
链接:www.matrix67.com/blog/archives/6039
(点击尾部阅读原文前往)
有没有一段代码,让你觉得人类的智慧也可以璀璨无比?
不一定要是完整算法,就是那种看着看着就觉得嗨爆了,惊为天人的结构或语句。
Kyle McCormick 在 StackExchange 上发起了一个叫做 Tweetable Mathematical Art 的比赛,参赛者需要用三条推这么长的代码来生成一张图片。具体地说,参赛者需要用 C++ 语言编写 RD 、 GR 、 BL 三个函数,每个函数都不能超过 140 个字符。每个函数都会接到 i 和 j 两个整型参数(0 ≤ i, j ≤ 1023),然后需要返回一个 0 到 255 之间的整数,表示位于 (i, j) 的像素点的颜色值。举个例子,如果 RD(0, 0) 和 GR(0, 0) 返回的都是 0 ,但 BL(0, 0) 返回的是 255 ,那么图像的最左上角那个像素就是蓝色。
参赛者编写的代码会被插进下面这段程序当中
(我做了一些细微的改动),最终会生成一个大小为 1024×1024 的图片。
// NOTE: compile with g++ filename.cpp -std=c++11
#include
#include
#include
#define DIM 1024
#define DM1 (DIM-1)
#define _sq(x) ((x)*(x)) // square
#define _cb(x) abs((x)*(x)*(x)) // absolute value of cube
#define _cr(x) (unsigned char)(pow((x),1.0/3.0)) // cube root
unsigned char GR(int,int);
unsigned char BL(int,int);
unsigned char RD(int i,int j){
// YOUR CODE HERE
}
unsigned char GR(int i,int j){
// YOUR CODE HERE
}
unsigned char BL(int i,int j){
// YOUR CODE HERE
}
void pixel_write(int,int);
FILE *fp;
int main(){
fp = fopen("MathPic.ppm","wb");
fprintf(fp, "P6\n%d %d\n255\n", DIM, DIM);
for(int j=0;j
for(int i=0;i
pixel_write(i,j);
fclose(fp);
return 0;
}
void pixel_write(int i, int j){
static unsigned char color[3];
color[0] = RD(i,j)&255;
color[1] = GR(i,j)&255;
color[2] = BL(i,j)&255;
fwrite(color, 1, 3, fp);
}
我选了一些自己比较喜欢的作品,放在下面和大家分享。
首先是一个来自 Martin Büttner 的作品:
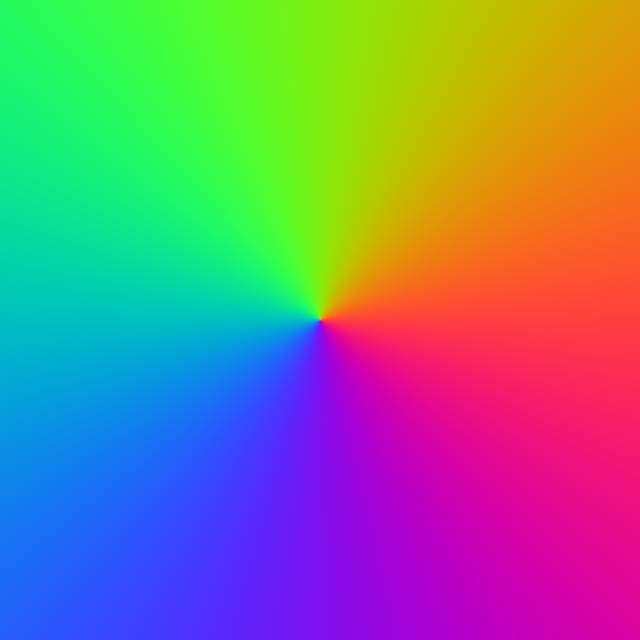
它的代码如下:
unsigned char RD(int i,int j){
return (char)(_sq(cos(atan2(j-512,i-512)/2))*255);
}
unsigned char GR(int i,int j){
return (char)(_sq(cos(atan2(j-512,i-512)/2-2*acos(-1)/3))*255);
}
unsigned char BL(int i,int j){
return (char)(_sq(cos(atan2(j-512,i-512)/2+2*acos(-1)/3))*255);
}
同样是来自 Martin Büttner 的作品:

这是目前暂时排名第一的作品。它的代码如下:
unsigned char RD(int i,int j){
#define r(n)(rand()%n)
static char c[1024][1024];return!c[i][j]?c[i][j]=!r(999)?r(256):RD((i+r(2))%1024,(j+r(2))%1024):c[i][j];
}
unsigned char GR(int i,int j){
static char c[1024][1024];return!c[i][j]?c[i][j]=!r(999)?r(256):GR((i+r(2))%1024,(j+r(2))%1024):c[i][j];
}
unsigned char BL(int i,int j){
static char c[1024][1024];return!c[i][j]?c[i][j]=!r(999)?r(256):BL((i+r(2))%1024,(j+r(2))%1024):c[i][j];
}
下面这张图片仍然出自 Martin Büttner 之手:

难以想象, Mandelbrot 分形图形居然可以只用这么一点代码画出
:
unsigned char RD(int i,int j){
float x=0,y=0;int k;for(k=0;k++4)break;}return log(k)*47;
}
unsigned char GR(int i,int j){
float x=0,y=0;int k;for(k=0;k++4)break;}return log(k)*47;
}
unsigned char BL(int i,int j){
float x=0,y=0;int k;for(k=0;k++4)break;}return 128-log(k)*23;
}
Manuel Kasten 也制作了一个 Mandelbrot 集的图片,与刚才不同的是,该图描绘的是 Mandelbrot 集在某处局部放大后的结果:

它的代码如下:
unsigned char RD(int i,int j){
double a=0,b=0,c,d,n=0;
while((c=a*a)+(d=b*b)
{b=2*a*b+j*8e-9-.645411;a=c-d+i*8e-9+.356888;}
return 255*pow((n-80)/800,3.);
}
unsigned char GR(int i,int j){
double a=0,b=0,c,d,n=0;
while((c=a*a)+(d=b*b)
{b=2*a*b+j*8e-9-.645411;a=c-d+i*8e-9+.356888;}
return 255*pow((n-80)/800,.7);
}
unsigned char BL(int i,int j){
double a=0,b=0,c,d,n=0;
while((c=a*a)+(d=b*b)
{b=2*a*b+j*8e-9-.645411;a=c-d+i*8e-9+.356888;}
return 255*pow((n-80)/800,.5);
}
这是 Manuel Kasten 的另一作品:

生成这张图片的代码很有意思:函数依靠 static 变量来控制绘画的进程,完全没有用到 i 和 j 这两个参数!
unsigned char RD(int i,int j){
static double k;k+=rand()/1./RAND_MAX;int l=k;l%=512;return l>255?511-l:l;
}
unsigned char GR(int i,int j){
static double k;k+=rand()/1./RAND_MAX;int l=k;l%=512;return l>255?511-l:l;
}
unsigned char BL(int i,int j){
static double k;k+=rand()/1./RAND_MAX;int l=k;l%=512;return l>255?511-l:l;
}
这是来自 githubphagocyte 的作品:

它的代码如下:
unsigned char RD(int i,int j){
float s=3./(j+99);
float y=(j+sin((i*i+_sq(j-700)*5)/100./DIM)*35)*s;
return (int((i+DIM)*s+y)%2+int((DIM*2-i)*s+y)%2)*127;
}
unsigned char GR(int i,int j){
float s=3./(j+99);
float y=(j+sin((i*i+_sq(j-700)*5)/100./DIM)*35)*s;
return (int(5*((i+DIM)*s+y))%2+int(5*((DIM*2-i)*s+y))%2)*127;
}
unsigned char BL(int i,int j){
float s=3./(j+99);
float y=(j+sin((i*i+_sq(j-700)*5)/100./DIM)*35)*s;
return (int(29*((i+DIM)*s+y))%2+int(29*((DIM*2-i)*s+y))%2)*127;
}
这是来自 githubphagocyte 的另一个作品:

这是一张使用 diffusion-limited aggregation 模型得到的图片,程序运行起来要耗费不少时间。代码很有意思:巧妙地利用宏定义,打破了函数与函数之间的界限,三段代码的字数限制便能合在一起使用了。
unsigned char RD(int i,int j){
#define D DIM
#define M m[(x+D+(d==0)-(d==2))%D][(y+D+(d==1)-(d==3))%D]
#define R rand()%D
#define B m[x][y]
return(i+j)?256-(BL(i,j))/2:0;
}
unsigned char GR(int i,int j){
#define A static int m[D][D],e,x,y,d,c[4],f,n;if(i+j
return RD(i,j);
}
unsigned char BL(int i,int j){
A;n;n++){x=R;y=R;if(B==1){f=1;for(d=0;d2){B=f-1;}else{++e%=4;d=e;if(!c[e]){B=0;M=1;}}}}}return m[i][j];
}
最后这张图来自 Eric Tressler :
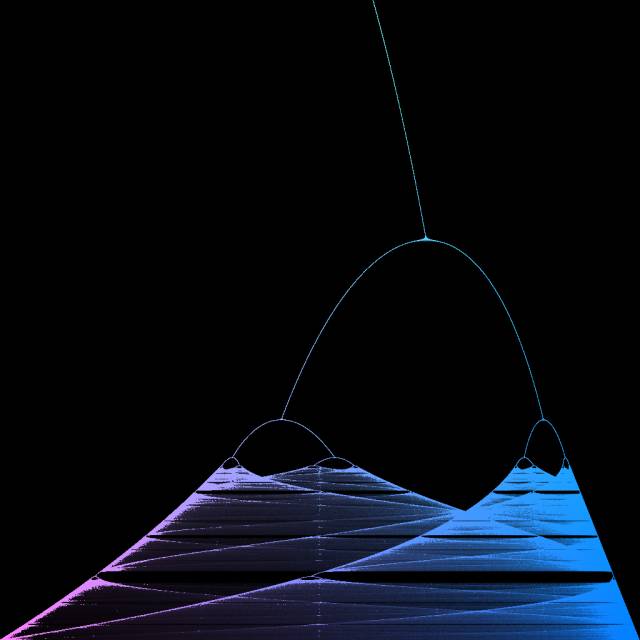
这是由 logistic 映射得到的 Feigenbaum 分岔图。和刚才一样,对应的代码也巧妙地利用了宏定义来节省字符:
unsigned char RD(int i,int j){
#define A float a=0,b,k,r,x
#define B int e,o
#define C(x) x>255?255:x
#define R return
#define D DIM
R BL(i,j)*(D-i)/D;
}
unsigned char GR(int i,int j){
#define E DM1
#define F static float
#define G for(
#define H r=a*1.6/D+2.4;x=1.0001*b/D
R BL(i,j)*(D-j/2)/D;
}
unsigned char BL(int i,int j){
F c[D][D];if(i+jD/2){e=a;o=(E*x);c[e][o]+=0.01;}}}}}R C(c[j][i])*i/D;
}

●
本文编号320,以后想阅读这篇文章直接输入320即可。
●输入m可以获取到文章目录。

Java编程
推荐
:
《
15个技术类公众微信
》
涵盖:程序人生、算法与数据结构、黑客技术与网络安全、大数据技术、前端开发、Java、Python、Web开发、安卓开发、iOS开发、C/C++、.NET、Linux、数据库、运维等。