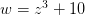复数可以阐释的如此优雅

点击上方 蓝色字体 ，关注我们

复数不仅有意义，而且可以用图示来 优雅 地解释。

1、实函数与数轴变换

大家都认识 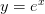，对于这样的初等函数，我们从小就学会使用 直角坐标系 来刻画它们：

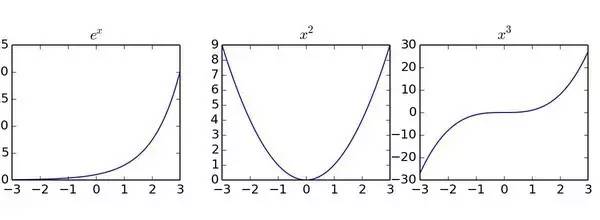
它们的 特点都大同小异 ： 把实数轴对应到实数轴 。然而，既然是一维函数，用二维图像来描述未免太过奢侈。如果我们把 数轴涂上不同颜色，再把一条新数轴上对应的函数值涂上相应颜色 ，就可以清晰地用它们的特点都大同小异：把实数轴对应到实数轴。然而，既然是一维函数，用二维图像来描述未免太过奢侈。如果我们把 数轴涂上不同颜色，再把一条新数轴上对应的函数值涂上相应颜色 ，就可以清晰地用 数轴-数轴 对应来展示函数这一关系：

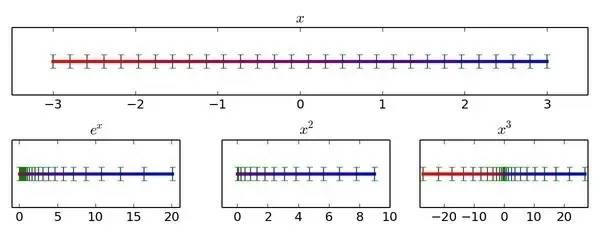
可以发现每个函数的作用无非是在有些地方把数轴往中间压了压，在有些地方又把数轴往两边扯了扯（观察图中小棒棒之间的间距是变窄还是变宽）：

• 越往左越挤压数轴，越往右越拉伸数轴

• 离0越远，对数轴的拉伸越厉害（在图上左半边图像和右半边图像重叠在了一起）。如果有一个小球在实数轴上向右滑行，那么它的像则先向左滑行到0，然后再向右滑行。

• 离0越远，对数轴的拉伸比楼上更厉害，但是不同的是，向右滑行的小球的像也一直向右滑行。

是挤压还是拉伸，就看函数在那一点的导数的绝对值是小于1还是大于1。 因此导数大小的意义就是局部小区间在变换下的伸缩倍数。 导数正负符号的意义是小区间是否反向 ，比如第二个函数在x小于0时导数也小于零，那么指向右方的数轴负数部分经过变换指向了左方。

2. 复数与平面变换

既然可以用上面的数轴-数轴对应来描述一维函数，那么类似地，就可以用 平面-平面 对应来描述二维函数。我们用一个复数表示平面上的点，用字母i区分纵坐标，就可以来研究复数函数 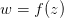的性质，其中 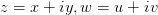。假设我们已经默认了复数的运算：

• 加法：

• 乘法：

• 极坐标分解： ，其中 是复数代表的平面向量到原点的距离， 是和横轴正方向的夹角。

拿出一个涂色的平面网格（从左上开始逆时针依次涂成红黄蓝绿色），把每个网点的像算出来，按顺序连起来，就可以来研究复函数了。

2.1. 复数的加法：

• 从图中可知，加法就是平面的平移，平移量恰好是那个复数对应的平面向量。
  

2.2 复数的乘法：

根据上面的运算法则很容易得到函数 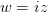的二维对应关系是 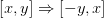，画在图上就是：

仔细看可以发现，各点乘以 的效果是平面逆时针旋转了90度，也就是 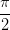弧度。

各点乘以 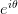的后果是平面逆时针旋转 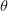弧度，这里是30度。

• 乘以一个一般的复数，就是把整个平面按它对应的角度旋转 弧度，再均匀放大 倍。

  
  

因此， 复数的加法就是自变量对应的平面整体平移，复数的乘法就是平面整体旋转和伸缩 ，旋转量和放大缩小量恰好是这个复数对应向量的夹角和长度。二维平移和缩放是一维左右平移伸缩的扩展，旋转是一个至少要二维才能明显的特征，限制在一维上，只剩下旋转0度或者旋转180度，对应于一维导数正负值（小线段是否反向）。

3. 复变函数与伸缩旋转

如果在每一个点处的旋转、放缩和平移量都不同（导数不同），就可以得到比较复杂的复数函数，举个例子：

3.1.

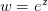
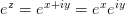，从上一小节的知识可知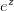， 的作用就是把平面上每个点按自己对应的坐标放大 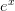倍、旋转 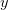弧度。我们立即可以猜测这个函数在x较大的地方放大的倍数更多，因为放大率 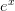更大；在x轴上只伸缩不旋转，因为没有 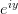旋转分量；在y轴上只旋转不伸缩，因为没有 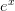放缩分量：

• 请看左图中的横向中轴，它在右图中的像也是横向中轴，只不过左边压缩，右边扩展，这正是我们一开始就提到的一维指数函数。而这个图， 恰好就是一开始那个数轴-数轴对应朝两边扩展形成平面-平面对应的结果。
  

• 再请看左图中的竖直中轴，它在右图发生了弯曲，贴在了单位圆周上，因此变成了一系列纯旋转的复数乘子。这一点在一维中可完全没有类似物，请谨慎类比。
  

• 其他点介于纯粹旋转和纯缩放之间。最后，请你回过头再仔细看看这幅图，你会发现这几段话也适用于图中的每个小正方形。小正方形变换前后的旋转和伸缩比例对应于函数的导数，本例中函数的导数就是原函数自己。

  
  

3.2.

• 加10就是整体向右平移10个单位，可以最后再看。
  

• 咱们来看 ,令 ,可以得到： ,这说明单位圆以内( )函数压缩，单位圆以外( )函数拉伸，离原点越远拉伸越厉害，正方形网格应该越来越大。