
以下文章内容,来自草堂君的新书《人人都会数据分析-从生活实例学统计》。因为新书中增添和细化了很多知识点,所以草堂君会逐步将这些内容补充到统计基础导航页中来,帮助大家建立数据分析思维。
限于篇幅,只截取书中部分内容
。
基础准备
前面为大家介绍了两种常见的离散型概率分布:二项分布及其实际生活应用和泊松分布及其实际生活应用。大家可以点击下方文章链接进行回顾:
今天要给大家介绍一种连续型概率分布:贝塔分布。贝塔分布是二项式分布的共轭先验分布,先验分布和后验分布是贝叶斯统计学研究的主要内容。下面首先了解什么是贝叶斯统计学。
贝叶斯统计
统计学有两大学派:经典统计学学派和贝叶斯学派,两种学派之间的最主要的争议在于是否利用主观概率。前面的文章介绍过,有三种确定概率的方法:古典概率法;统计概率法(频数法);主观概率法。经典统计学派使用的概率为古典概率法和统计概率法(频数法)确定的概率,因为总体情况经常未知,所以频数法又更为常用,由此可见,经典统计学派认为只有“客观”的概率(古典概率法和频数概率法确定的概率)才符合科学要求,才能用于统计分析,而主观概率是“主观的”,顶多对个人决策有用,用于科学的数据统计推断会导致错误。贝叶斯学派却不这样认为,它们认为除了古典概率法和频数法确定的概率以外,主观概率法确定的概率也应该在统计分析中被充分利用,否则是一种极大的浪费。
贝叶斯统计学派将经验和历史资料等信息称为先验信息,如何将人们的经验和过去的历史资料确定概率和先验分布是贝叶斯学派要研究的问题。贝叶斯统计学派认为通过经验和历史资料获得的主观概率对统计推断是有益的,例如,一位从事金银首饰生意十几年的金器店主声称,他能快速辨别出金银首饰的真假,为此进行了
10
次试验,他都做出了正确的判断。在这个试验中,如果认为店主是在猜测,那么每次正确判断的概率仅为
50%
,
10
次都正确的概率为
0.5
10
=0.0009766
,这是一个非常小的概率,几乎不可能发生,因此可以推断店主每次成功判断的概率远远高于
50%
,他不是在猜测,而是利用经验极大提高了判断准确率。
先验分布与后验分布
贝叶斯学派认为任何未知量都可以看作一个随机变量,都应该用一个概率分布去描述,根据概率分布获取途径的不同,可以分为先验分布和后验分布。先验分布是分析者在通过试验获取数据前,根据过去对未知量的认识而确定的概率分布;后验分布是通过抽样(试验),收集未知量的信息,对先验分布进行优化调整后的概率分布。
还有一个共轭先验分布的概念,草堂君也希望大家了解其含义。例如,某未知变量的先验分布为贝塔分布,用贝叶斯估计算得的后验分布仍然是贝塔分布,只是其中的参数不同,那么这样的先验分布(贝塔分布)称为未知变量的共轭先验分布。
贝塔分布
贝塔分布是二项分布的共轭先验分布,其推导过程如下:设某事件A在一次试验中发生的概率为q,为了对该概率做出估计,进行n次独立试验,事件A发生x次,显然概率服从二项分布,表示为:

如果在试验前对事件A没有了解,那么对其发生的概率q也没有任何信息。面对此种局面,贝叶斯采用“同等无知”的原则,认为事件A发生的概率q有同等机会取(0,1)区间内的任意值,也就是将均匀分布U(0,1)作为事件A发生概率q的先验分布。因此事件A发生概率q的先验分布可以表示为:
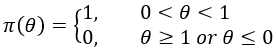
结合试验信息和先验分布,利用贝叶斯公式可以求出事件A发生概率q的后验分布,具体如下:

由此可见,贝塔分布是描述某个事件发生概率的概率分布,有点绕口,大家好好理解一下。需要注意,当贝塔分布的两个参数都为
1
时,也就是
Beta(1,1)
,是等于前面的先验分布,均匀分布
U(0,1)
的。这也就验证了贝塔分布是二项分布的共轭先验分布。
贝塔分布性质
贝塔分布是一个定义在[0,1]区间上的连续概率分布族,它有两个正值参数,称为形状参数,一般用α和β表示。贝塔分布的概率密度函数形式如下:

贝塔分布的均值与方差为:
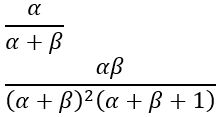
贝塔分布的概率密度函数
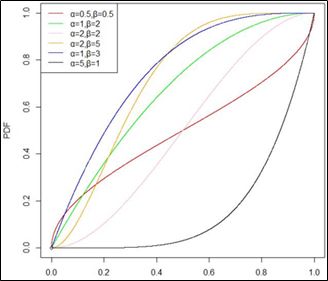
从贝塔分布的概率密度函数的图形可以看出,贝塔分布曲线有很多,随着形状参数α和β的改变而改变,但都是在(0,1)区间内。贝塔分布适合用于某事件发生或者成功概率的建模。
生活实例
贝叶斯学派的关键人物拉普拉斯曾经做过一个著名的试验,用于验证研究男婴的诞生比例是否大于0.5。他随机抽取了493472名婴儿,并登记他们的性别,发现其中有251527个男婴, 241945个女婴。他选用均匀分布U(0,1)作为男婴诞生概率θ的先验分布,于是得到男婴诞生概率θ的后验分布Beta(x+1,n-x+1)/ Beta(α,β)。
分析思路
要验证男婴诞生比例是否大于0.5,可以通过男婴诞生比例θ的后验分布,计算θ<=0.5的概率,如果计算出来的男婴诞生比例θ<=0.5的概率非常小,说明男婴诞生比例大于0.5是几乎可以肯定的事实。
分析过程
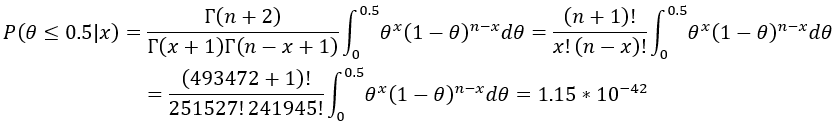
从结果可知,男婴出生概率小于0.5的概率是非常小的,仅为1.15*10^-42,因此拉普拉斯断言男婴的出生概率大于50%。
温馨提示:












