经典信用评分与机器学习应用思考

主要观点：

1 、经典信用评分卡是基于逻辑回归的二分类模型，在变量处理方面采用WOE可以保证特征变量与目标变量之间的单调关系。在建模构建过程中，评分卡模型有着严谨的统计学理论基础做支撑。评分卡建模可以在很多场景，对于正负样本的定义对应着模型的不同应用场景。

2 、机器学习能够适用于高维稀疏和弱关系变量数据，对于模型细分和自适应学习方面可以节省大量人力成本，但机器学习模型复杂度高，需要建立更加完善的监控和迭代优化体系。

3 、根据不同的业务目标、数据质量和应用场景选择合适的建模工具才能实现经典评分卡模型与机器学习模型的优势互补，不断提高风险计量水平。

一、经典信用评分卡介绍

经典 信用评分的本质是基于逻辑回归的二分类模型，所以对经典信用评分的介绍就可以从两个方面着手，一个是逻辑回归，一个是二分类。逻辑回归决定了评分卡的技术内核，分类方式决定了评分卡的应用场景。

1.1 逻辑回归与评分转换

逻辑回归是统计学回归方法的一种，线性回归模型是对连续型目标变量进行预测，而逻辑回归的目标变量取值为0和1，代表不同的类别。针对0-1变量，回归函数应改用限制在[0,1]区间内的连续曲线，而不能再沿用线性回归方程，所以在线性回归模型基础上，应用Logistic分布函数进行变换，将结果投射为[0,1]区间内的连续曲线。逻辑回归可以表示成如下的参数化的Logistic条件概率分布：

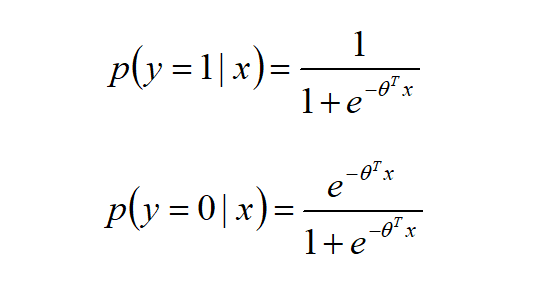
基于二项分布构造极大似然估计，应用梯度下降法即可以求解回归系数向量 θ 。对上式进行变换得到：

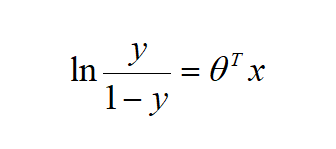
如果定义y是坏客户的比率，那么odds=y/(1-y)即为坏样本与好样本的比值，计算回归系数后，逻辑回归直接得到的是坏客户与好客户的比值的自然对数。如果要以分数形式展现，必须经过转换，其公式为

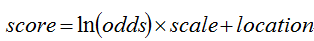
设定odds=1:1时的分数，假定为600分，设定odds每增加1倍，相对减少的分数，假设为20分，将odds=1:1及2:1时的分数套入公式，得到下列两式

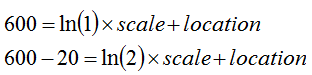
求解得到 location=600，scale=-20/ln(2) ，从而

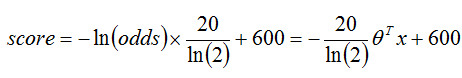
注意到score是一个和式，我们也可以将最后的得分看做是各个变量得分的加和，每一个特征维度都可以计算一个得分，这便有了评分卡的概念。

1.2 变量处理与WOE

在变量的处理方面，首先应该想到的是分类变量的处理，通常分类变量的取值没有实际的数值意义，比如地域和学历。一个常用的办法是使用哑变量，将一个变量编译为n-1个变量（n是分类变量的取值个数），这也是大部分统计教材中介绍的方法。哑变量的编码方式会带来两个问题：

首先是特征变量的维度会增加，如果考虑区域变量的话，一个变量就会衍生出几十个变量。这些变量都是二值变量，由于一个客户只能属于一个区域，所以得到的区域的衍生变量矩阵是非常稀疏的，逻辑回归不太擅长处理这类变量。

其次是模型的可解释性，建模之前和建模过程中都需要经过变量筛选，仍然以区域举例，极有可能出现的一种情况是区域的衍生变量中某几个进入到了最终的模型，大部分变量被筛掉了。区域变量的信息不完整，模型展现的结果就是只考虑某几个区域。上文中提到，评分卡模型是在每一个特征变量上进行评分，进行加和得到最后的评分。如果进入到模型的区域变量是A、B、C、D，那么对于一个来自区域E的客户，就要给他打出非A、非B、非C、非D四个得分，由于没有进入到模型，作为区域E的得分便无法得到。这对于模型的使用者尤其是不太了解建模过程的业务人员来说，是一件困惑的事情。

通常评分卡建模对于分类变量数值化的办法是使用WOE，WOE的计算方法如下：

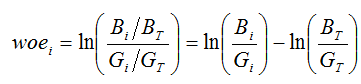
其中 B _i 是第i类取值下的坏样本数， B _T 为全量样本下的坏样本数， G _i 是第i类取值下的好样本数， G _T 为全量样本下的好样本数。不难看出，WOE可以反映出某一类取值项下的好坏样本比与整体的关系，如果该类项下坏客户占比高于整体水平，那么WOE值为正值，且坏客户占比越高，WOE值越大。一方面，WOE可以作为同一变量不同取值下的客群的质量评价指标，即WOE越高，则说明该客群质量越差；另一方面，如果不同取值下的WOE值差异较大，就可以说明变量对目标变量的解释性越好。通常使用IV值来表征特征变量对目标变量的可解释程度，IV可以作为变量筛选的一个参考。IV值得计算如下：

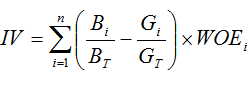
建模时，将分类变量的值用对应的WOE值替代，由于WOE的计算过程加入了特征变量的信息，可以保证的是进行WOE替换后的特征变量与目标变量的单调关系，即特征变量WOE值越大，目标变量取1的概率越高。正是由于有这样的好处，连续变量也有必要进行分段处理，然后用WOE值进入模型。以年龄为例，在信贷业务中，年龄太小或年龄太大的客户坏账率都比较高，也就是坏账率与年龄的关系是U字形的，如果直接将客户的年龄作为变量，这种非线性的关系就不能反映出来，模型的效果也会受到影响。对年龄分组后，就可以计算不同年龄段对应的WOE；相对于原来的年龄变量，分段后的WOE可以看做是重排序，将U字形关系变成了单调性关系。

连续变量分段还有一个好处就是可以将极值纳入到分段中，防止变量的过拟合。另外，缺失值也可以单独作为一类，计算WOE进入模型，不必进行缺失值填充。对于连续变量的分组方法，可以采用等值或等频分段的方法，结合业务经验确定分组边界；也可以使用最优化算法，比如寻找分界点使得分段后的变量IV值尽可能大。需要注意的是，由于WOE的计算加入了目标变量的信息，为了保证模型的稳定性，分段时各段的样本量不能太少，可以将WOE相近的段进行合并。

1.3 评分卡应用

数值变量分段后，与分类变量一样进行WOE计算，然后建立逻辑回归模型，采用逐步回归建立模型，所有变量通过显著性检验和业务解释后就可以得到评分卡。假设一个只考虑性别和年龄的评分卡模型，确定 location=600，scale=-20/ln(2) ，那么得到的评分卡举例如下：

上表中各子项的评分计算为WOE*系数*scale，评分卡在应用时只需要根据客户各个特征的取值在location的基础上进行加减分即可。比如一个男性、20岁的客户，评分就是-6.6-5.0-5.2+600=583.2。

1.4 不同业务场景的评分卡

二分类就是建模中的目标变量分为正类和负类，一般正类就是我们的关注类。正类和负类的划分需要有明确的业务含义。评分卡建模工作可以分为六个部分，分别是业务理解、数据理解、数据预处理、模型构建、模型评估和模型部署；其中业务理解和模型部署作为建模工作的起点和终点，都与业务有着紧密的联系。

按照应用场景的不同，信用评分可以分为申请评分模型、行为评分模型和催收评分卡模型。对于申请评分模型和行为评分模型来说，正、负样本类的业务定义就是违约和非违约；对于催收评分模型来说，由于进入到催收阶段的客户都是违约客户，所以催收模型的正样本就是不还款继续变坏的客户。

当然，评分卡模型可以应用的范围不止信用评估方面，比如客户流失预测模型中，正样本就是流失的客户；在广告点击预测中，正样本是点击广告的客户；在个性化商品推荐中，正样本就是浏览或购买商品的客户。诸如此类应用模式，不一而足。

有些模型中，好坏样本是容易定义的。比如滚动率预测模型是催收评分模型的一种，对于M1-M2滚动率预测模型来说，全量客户就是处于M1的客户，正类样本就是进入M1后一个月内未还款进入M2逾期的客户。而对于申请评分模型，由于客户获得信用卡后，风险暴露需要一定的时间，可能是6个月、12个月、18个月甚至更长，这就需要设置一个阈值，也就是表现期，定义在这个表现期内违约的客户为正类样本。对于会员流失预测模型，客户会员到期后可能过几天就会续费接着购买会员，所以到期后多长时间内不续费才算流失。对于收益评估模型，要定义一个阈值，收益高于这个金额阈值的客户为正样本类，这些阈值是需要通过数据分析得到的。样本分类完成后，就可以着手数据处理和模型构建的过程了，最后的模型部署也要参考样本分类时的业务定义。

二、机器学习在信用评估中的应用