(点击上方公众号,可快速关注)
转自:刘毅
https://www.61mon.com/index.php/archives/215/
好文投稿, 请点击 → 这里了解详情
一:背景
字典树,又称前缀树(英文名:Trie Tree),为 Edward Fredkin 发明。
举个例子,给出一些单词,(and,as,at,cn,com),则其字典树如下:
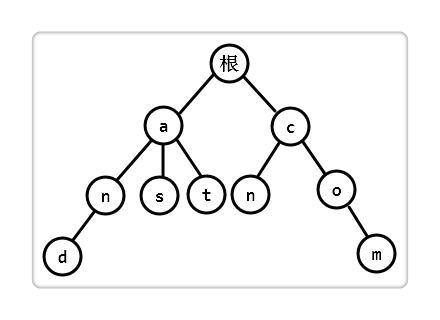
从上图可以发现,它有 3 个基本性质:
1、根结点不包含字符,除根结点外每一个结点都只包含一个字符。
2、从根结点到某一结点,路径上经过的字符连接起来,为该结点对应的字符串。
3、每个结点的所有子结点包含的字符都不相同。
字典树是一个很重要的数据结构,其主要应用为:
1、词频统计:例如,给定一个由 10 万个单词组成的库,现要你判断一个单词是否有在库中出现,若出现,求出共出现多少次。
2、前缀匹配:以上图为例,如果想获取所有以 "a" 开头的字符串,那么从图中可以很明显的看到是:(and,as,at)。因此利用这个特性,可以巧妙地实现搜索提示功能,如输入一个网址,可以自动列出可能的选择。当没有完全匹配的搜索结果,可以列出前缀最相似的可能。
二:算法过程分析
共实现三个对外接口:
1、void add(char * s);:将字符串 s 添加至字典树;
2、int query(char * s);:查询字符串 s 是否存在。若存在,返回其存在的次数;若不存在,返回 0;
3、bool remove(char * s);:删除字符串 s。字符串 s 若存在,则直接删除,返回真;若不存在,则返回假。
结点结构如下:
#define TREE_WIDTH 26
struct Node
{
int path;
int end;
char ch;
Node * next[TREE_WIDTH];
Node(char ch = ' ')
{
this->ch = ch;
this->path = this->end = 0;
for (int i = 0; i < TREE_WIDTH; i++)
this->next[i] = nullptr;
}
};
本文只讨论小写 26 个英文字母的字典集合,故TREE_WIDTH设为 26。
变量end的作用,标记该结点是否是单词结尾。变量path则用来记录结点被路径覆盖的次数。
请注意,下述代码针对的是动态数据集,即一系列添加,查询,删除三种混合操作。因此对于已无路径覆盖的结点,我们并不会释放其内存,这也是引入path的原因(当path = 0,表示该结点已无路径覆盖)。
两个变量的具体使用如下图:
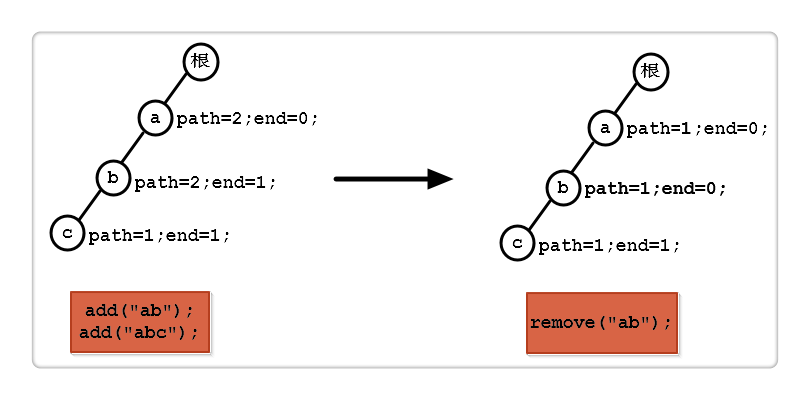
三:完整代码
/**
*
* author : 刘毅(Limer)
* date : 2017-08-08
* mode : C++
*/
#include
#define TREE_WIDTH 26
using namespace std;
struct Node
{
int path;
int end;
char ch;
Node * next[TREE_WIDTH];
Node(char ch = ' ')
{
this->ch = ch;
this->path = this->end = 0;
for (int i = 0; i < TREE_WIDTH; i++)
this->next[i] = nullptr;
}
};
class TrieTree
{
private:
Node * root;
public:
TrieTree();
~TrieTree();
void destroy(Node * t);
void add(char * s);
int query(char * s);
bool remove(char * s);
};
TrieTree::TrieTree()
{
root = new Node;
}
TrieTree::~TrieTree()
{
destroy(root);
}
void TrieTree::destroy(Node * t)
{
for (int i = 0; i < TREE_WIDTH; i++)
if (t->next[i])
destroy(t->next[i]);
delete t;
}
void TrieTree::add(char * s)
{
Node * t = root;
while (*s)
{
if (t->next[*s - 'a'] == nullptr)
t->next[*s - 'a'] = new Node(*s);
t->next[*s - 'a']->path++;
t = t->next[*s - 'a'];
s++;
}
t->end++;
}
int TrieTree::query(char * s)
{
Node * t = root;
while (*s)
{
if (t->next[*s - 'a'] == nullptr || t->next[*s - 'a']->path == 0)
return 0;
t = t->next[*s - 'a'];
s++;
}
return t->end;
}
bool TrieTree::remove(char * s)
{
if (query(s))
{
Node * t = root;
while (*s)
{
t->next[*s - 'a']->path--;
t = t->next[*s - 'a'];
s++;
}
t->end--;
return true;
}
return false;
}
int main()
{
TrieTree tree;
tree.add("strawberry");
tree.add("grandfather");
tree.add("policeman");
tree.add("breakfast");
tree.add("mutton");
tree.add("bus");
tree.add("bus");
tree.add("bustop");
tree.add("computer");
// test "query"
cout << tree.query("bud") << endl; // 0
cout << tree.query("bus") << endl; // 2
// test "remove"
tree.remove("bustop");
cout << tree.query("bustop") << endl; // 0
tree.remove("bus");
cout << tree.query("bus") << endl; // 1
tree.remove("bus");
cout << tree.query("bus") << endl; // 0
return 0;
}
四:不足及改进
我们发现,每个结点,其内部都有一个指针数组,在稀疏树下,大多空间被浪费。
因此针对上面问题,人们提出了两种改进结构:二数组字典树和三数组字典树。具体可阅本系列第二篇。
觉得本文有帮助?请分享给更多人
关注「算法爱好者」,修炼编程内功
















