中药浸膏粉离散元模拟参数标定方法研究

摘  要 ： 目的 采用离散元法（ DEM ）模拟中药浸膏粉休止角，确定颗粒之间、颗粒与几何体之间的接触参数。 方法 以生甘草浸膏粉、独活浸膏粉、微晶纤维素（ MCC ）和乙基纤维素（ EC ） 4 种粉末为研究对象，在 Hertz-Mindlin with JKR Cohesion 接触模型和颗粒缩放的基础上，通过 Plackett-Burman 设计筛选出对休止角模拟测定影响显著的接触参数，进而通过最陡爬坡设计确定关键接触参数的最佳区域。根据 Box-Behnken 试验结果，建立接触参数和模拟休止角之间的回归模型，优选最佳接触参数值并验证。 结果 筛选得到的关键接触参数为颗粒 - 颗粒滚动摩擦系数、颗粒 - 颗粒恢复系数和颗粒 - 不锈钢恢复系数，所建回归模型对休止角的标定范围为 33.30° ～ 43.64° ， 4 种粉末休止角模拟测定值与实验值的相对误差绝对值均小于 2.0% ，表明所建标定方法准确可靠。 结论 证明了通过宏观物性参数间接标定中药颗粒体系 DEM 微观力学参数的可行性，为混合、输送等中药制药过程的精确模拟奠定了基础。

离散元法（ discrete element method ， DEM ）是解决非连续介质问题的数值模拟方法。 DEM 将求解空间离散为单元，并模拟所有单元在任意时刻的位移、速度、加速度、角速度等物理量，进而预测离散群体行为，被广泛应用于岩土、建筑、农业和医药等领域颗粒体系的过程模拟和装备设计等 ^[1-4] 。 DEM 运行原理为（ 1 ）在单个时间步长内使用接触模型计算相邻颗粒或者几何体对每个颗粒施加的作用力；（ 2 ）根据牛顿第 2 定律计算颗粒的速度和旋转速度；（ 3 ）根据时间步长计算颗粒的新位置。这一过程在每个时间步长中应用于每个颗粒，并重复至模拟结束 ^[5] 。近年来，高性能计算的发展极大提高了 DEM 计算效率，可支持百万级和千万级单元的动态仿真 ^[6] ，使之更接近工程实际。 DEM 耦合计算流体力学（ CFD ）、多体动力学（ MBD ）和有限元法（ FEM ）可实现复杂颗粒体系的多学科仿真 ^[7-9] 。

在制药工程领域， DEM 已应用于粉末混合、输送、制粒和压缩等口服固体制剂的制备过程。 Park 等 ^[10] 使用 DEM 对 5 种具有不同桨叶角度设计的连续混合器中双峰分布颗粒的混合过程进行了模拟，提出轴向和横向方差指数以评估颗粒混合均匀度，并指导不同给料条件下的混合器螺杆桨叶角度设计。 Mazor 等 ^[11] 以微晶纤维素（ MCC ） PH 101 为研究对象，采用 DEM 模拟干法制粒进料区的颗粒流动，采用 FEM 模拟 MCC 在辊压区的形变， DEM 与 FEM 联用可以更好的预测螺杆转速和辊轮转速对薄片密度和均匀性的影响。

中药浸膏粉成分复杂，具有易吸湿、黏性大、流动性差等特点 ^[12] ，在 DEM 模拟中缺乏相应仿真参数的报道。 DEM 仿真参数主要指颗粒与颗粒之间、以及颗粒与设备几何体之间的接触参数，如恢复系数、静摩擦系数、滚动摩擦系数等。通常来说，接触参数难以由实验测定，一般通过改变参数值并进行模拟，将模拟结果与真实实验结果进行对比，直到模拟结果与实验结果一致 ^[13] 。为了提高 DEM 在中药制药领域的适用性，本实验以粉末休止角（ α ）的测定过程为例，对接触参数进行标定，研究结果可为中药粉体混合和输送等制剂过程精细化设计奠定基础。

1 材料

生甘草浸膏粉（批号 180421-20180101094 ）、独活浸膏粉（批号 180423-445800-18 ）均由北京康仁堂药业有限公司提供，通过水提、浓缩和喷雾干燥工艺制备。 MCC Vivapur ^® type 200 ，批号 5620030813 ，上海昌为医药辅料技术有限公司；乙基纤维素 N100 Pharm ，批号 44547 ， Ashland Inc. 。

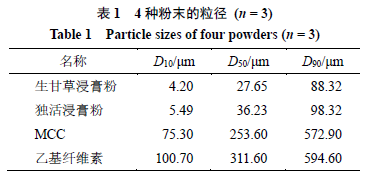
使用 BT-2001 激光粒度分布仪（丹东百特仪器有限公司）对上述 4 种粉末的粒径分布进行测定，累积粒径分布达 10% 、 50% 、 90% 所对应的粒径值 D ₁₀ 、 D ₅₀ 、 D ₉₀ 见表 1 。

2 模拟方法

2.1 接触模型

接触模型是在离散元模拟时颗粒之间相互作用力计算的依据，涉及到了颗粒的表面黏连、接触、变形等。接触模型可根据对研究对象特性的理解进行选择。中药粉末具有一定黏性，因此在本实验中选用 Hertz-Mindlin with Johnson-Kendall-Roberts （ JKR ） Cohesion 接触模型 ^[14] ，该模型为凝聚力接触模型，在接触区域中考虑了液桥力、范德华力等的影响，适于模拟强粘性系统，如细干颗粒或湿颗粒等。在 Hertz-Mindlin with JKR Cohesion 接触模型中，颗粒间的切向阻尼力可由式（ 1 ）求出。

F _t ＝ −2(5/6) ^1/2 β ( S _t m ^* ) ^1/2 v _t ^rel （ 1 ）

m ^* 为等效质量， v _t ^rel 是切向相对速度，系数 β 和切向刚度 S _t 可由下面 2 式求出。

β ＝ ln e /(ln ² e ＋ π ² ) ^1/2 （ 2 ）

S _t ＝ 8 G ^* ( R ^* α ) ^1/2 （ 3 ）

e 为恢复系数， G ^* 为等效剪切模量， R ^* 为等效粒子半径

切向力与摩擦力 μ _s F _n 有关，此处 μ _s 为静摩擦系数，滚动摩擦可以通过接触表面上的力矩来说明。

T _i ＝ − μ _r F _n R _i ω _i （ 4 ）

μ _r 为滚动摩擦系数， R _i 为质心到接触点的距离， ω _i 为接触点处物体的单位角速度矢量

通过选择接触模型、设置接触参数、以及设置几何体物理模型，可对颗粒体系的运动行为进行 DEM 模拟。

2.2 颗粒缩放

颗粒粒径和形状的设置影响模拟的计算速度，本实验采用的中药粉末由喷雾干燥工艺制得，粒径较小且接近球型，为了提高离散元仿真的效率并节约计算时间，将模拟颗粒形状设置为球形。对于由大量微小颗粒组成的粉体系统的模拟通常采用放大颗粒的方法。 Feng 等 ^[15] 提出了颗粒缩放应当遵循 3 个相似原理：几何相似、运动相似、动力相似。几何相似指缩放模型必须严格遵守经典的几何相似性原理，运动相似是指模型与原型中对应点处的速度方向相同，大小成比例，并且具有同一比率；运动相似还要求对应时间间隔成比例并具有同一比率。动力相似是指模型和原型受到相同性质力的作用，并且这些力成比例并具有同一比率。本实验将表 1 中 4 种粉末的颗粒半径均放大为 1 mm 进行后续的模拟试验。

3 粉体休止角试验测定和模拟测定

3.1 休止角实验测定

休止角测定参照《欧洲药典》第 10 版 2.9.16 节，具体操作如下：使用 BEP2 粉体流动性测试仪（英国 Copley 公司），固定底面圆盘，圆盘直径（ Φ ）为 100 mm ，将粉末从喷嘴上方的漏斗缓慢倒入，喷嘴直径为 10 mm ，喷嘴下端距离底面圆盘的高度为 75 mm 。粉末在底面圆盘形成锥体，当锥体高度不再增加时，读取锥体高度（ h ）和底面圆盘的半径（ r ），平行测量 3 次，求平均值，休止角 α （ ° ）的计算公式如下。

α ＝ arctan( h / r ) （ 5 ）

3.2 休止角模拟测定

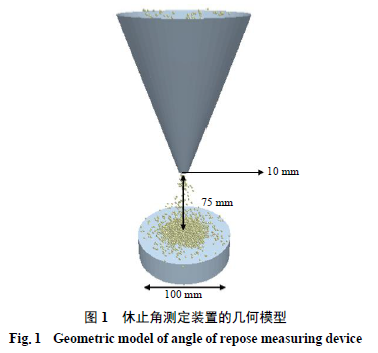
构建 BEP2 粉末流动性测试仪漏斗和底座部分的几何模型，如图 1 所示。使用离散元模拟软件 EDEM2018 （ DEM SolutionsLtd. ， Edinburgh ）进行研究。放大颗粒半径设置为 r ＝ 1 mm ，颗粒生成方式为 Dynamic （即动态生成），生成的总量为 100 g ，产生的颗粒数量为 2 000 个 /s 。待 100 g 的颗粒全部堆积在底面圆盘上并形成堆积的锥体后，采用软件后处理中记录颗粒位置的功能，记录颗粒堆积最高位置随时间变化的趋势，当两个时刻颗粒的高度变化≤ 0.2% ，认为颗粒的堆积相对静止，记录此时锥体的高度 h 并根据式（ 5 ）计算休止角。

4 休止角模拟过程实验方法设计

使用离散元模拟需要设置颗粒、几何体的材料参数，以及颗粒 - 颗粒、颗粒 - 几何体的接触参数。颗粒材料参数包括：颗粒粒径、颗粒密度、颗粒形状、泊松比、剪切模量。几何体物理参数包括密度、剪切模量、泊松比等，由于使用的休止角测量实验工具为不锈钢材质，因此直接使用不锈钢的模拟参数，见表 2 。 EDEM 软件接触参数包括颗粒 - 颗粒恢复系数、颗粒 - 颗粒静摩擦系数、颗粒 - 颗粒滚动摩擦系数、颗粒 - 不锈钢恢复系数、颗粒 - 不锈钢静摩擦系数、颗粒 - 不锈钢滚动摩擦系数以及反映物料粘性的 JKR 表面能。

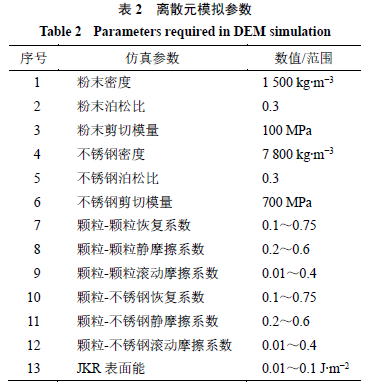
结合文献对药物粉末与不锈钢材料离散元模拟的参数设置 ^[16-18] 以及本课题组建立的中药原辅料物性数据库 ^[19] ，设置模拟参数和（或）参数变化范围如表 2 所示。其中粉末泊松比 0.3 ，固体密度为 1 500 kg/m ³ ，剪切模量 100 MPa 。表 1 中 4 种粉末与几何体的接触参数与模拟材料的密度、形状、粒径等性质有关，文献资料尚无报道，且并非每个接触参数 对模拟结果都有显著性影响，因此，由标定方法获得 ^[20] 。首先采用 Plackett-Burman 试验从 7 个接触参数中筛选出对休止角模拟影响较大的参数，之后进行最陡爬坡试验使得模拟休止角结果进入最佳区域，最后通过 Box-Behnken 试验优化确定模拟休止角的最佳接触参数。

5 结果与分析

5.1 Plackett-Burman 试验

Plackett-Burman 设计是一种 2 水平（ −1 和 +1 水平）的试验设计方法，它试图用最少试验次数筛选并确定对结果影响比较显著的因素。本实验 Plackett-Burman 设计以粉末休止角为响应值，对影响模拟且不易确定的 7 个接触参数颗粒 - 颗粒恢复系数（ particle-particle restitutioncoefficient ， A ）、颗粒 - 颗粒静摩擦系数（ particle-particle static friction coefficient ， B ）、颗粒 - 颗粒滚动摩擦系数（ particle-particle rolling friction coefficient ， C ）、颗粒 - 不锈钢恢复系数（ particle-stainless steelrestitution coefficient ， D ）、颗粒 - 不锈钢静摩擦系数（ particle- stainless steelstatic friction coefficient ， E ）、颗粒 - 不锈钢滚动摩擦系数（ particle-stainless steelrolling friction coefficient ， F ）和 JKR 表面能（ Johnson Kendall Roberts surfaceenergy ， G ）进行筛选。 Plackett-Burman 试验因素水平表如表 3 所示，采用 Design Expert 8.0.6 软件（ Stat-Ease, Inc ， United States ）生成 13 次试验，使用“ 3.2 ”项方法进行休止角模拟测定，试验设计方案及结果见表 3 。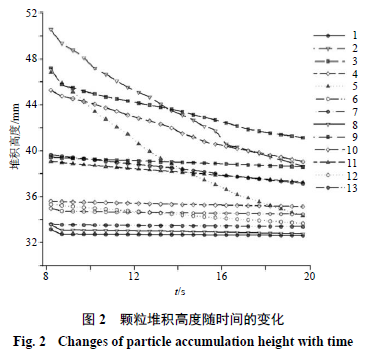颗粒全部下落后，堆积高度随时间的变化曲线见图 2 。图 2 中，曲线起点表示在 8.2 s 时颗粒全部生成，曲线终点表示模拟的休止角测定总时间为 20 s 。

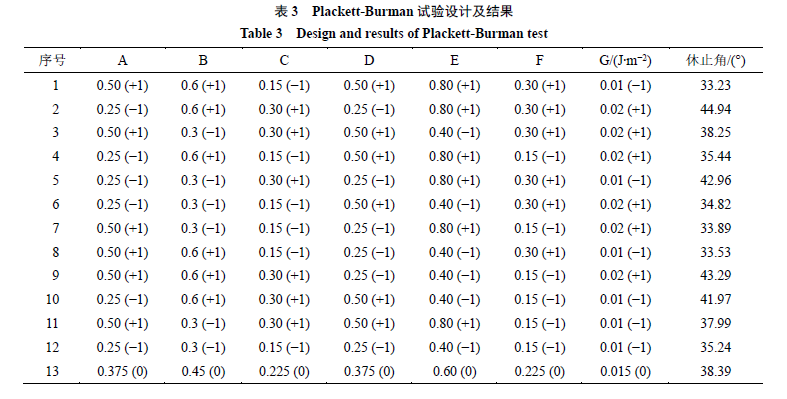
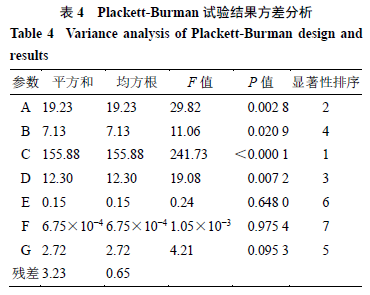
对表 3 模拟的结果进行方差分析，结果如表 4 所示。可见，颗粒 - 颗粒滚动摩擦系数、颗粒 - 颗粒恢复系数、颗粒 - 不锈钢恢复系数的 P 值小于 0.01 ，对粉末休止角的模拟结果影响极其显著；颗粒 - 颗粒静摩擦系数的 P 值 ＜ 0.05 ，对粉末休止角的模拟结果影响显著；其余 3 个因素的 P 值＞ 0.05 ，对粉末休止角的模拟结果影响较小。在后续的最陡爬坡试验以及 Box-Behnken 实验中选择 3 个对休止角的模 拟影响极其显著（ P ＜ 0.01 ）的因素；根据已有的研究以及作者对于药物粉末的理解 ^[21-23] ，将其余参数的数值固定为：颗粒 - 颗粒静摩擦系数 0.6 、颗粒 - 不锈钢静摩擦系数 0.4 、颗粒 - 不锈钢滚动摩擦系数 0.15 、 JKR 表面能 0.01 来进行后续的试验设计。

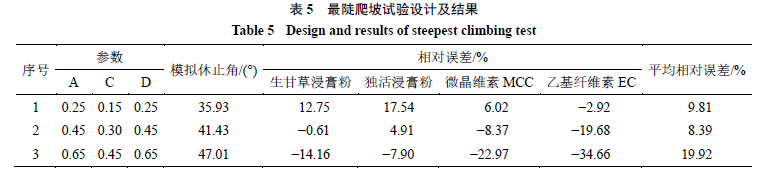
5.2 最陡爬坡试验

Plackett-Burman 试验后，根据筛选出的对模拟影响显著的因素，进行最陡爬坡试验，以便能够快速进入最佳的响应区域。本实验颗粒 - 颗粒恢复系数（ A ）爬坡步长设定为 0.2 ，颗粒 - 颗粒滚动摩擦系数（ C ）爬坡步长设定为 0.15 ，颗粒 - 不锈钢恢复系数（ D ）爬坡步长设设定为 0.2 ，最陡爬坡试验设计如表 5 所示。采用“ 3.1 ”项的方法进行休止角实验测定，生甘草浸膏粉、独活浸膏粉、 MCC 和乙基纤维素的休止角实测值分别为 41.18 ° 、 43.57 ° 、 38.23 ° 、 34.91 ° 。根据 EP 10.0 休止角大小和粉体流动性的关系，生甘草浸膏粉和独活浸膏粉的休止角在 41 ° ～ 45 ° ，属于流动性尚可、可处理的范畴； MCC 休止角在 36 ° ～ 40 ° ，表明流动性适当、无需辅助的范畴；乙基纤维素休止角在 31 ° ～ 35 ° ，说明其流动性良好。

采用“ 3.2 ”项的方法进行休止角模拟测定，结果如表 5 所示。分别计算 4 种粉末休止角和模拟休止角的相对误差＝ ( 实验休止角 － 模拟休止角 )/ 实验休止角，然后计算 4 种粉末分别在每个实验条件下的平均相对误差，结果 1 ～ 3 号实验的平均相对误差分别为 9.81% 、 8.39% 、 19.92% 。可见在 1 、 2 号水 平的平均相对误差较小，且有 3 种粉末的实验测定休止角落在了 1 号水平和 2 号水平的范围内，因此在后续的 Box-Behnken 试验中以 1 号水平为低水平， 2 号水平为高水平进行休止角模拟测定实验。

5.3 Box-Behnken 试验及回归模型

根据“ 5.2 ”项确定的因素范围，对颗粒 - 颗粒恢复系数、颗粒 - 颗粒滚动摩擦系数、颗粒 - 不锈钢恢复系数 3 个因素进行 Box-Behnken 试验设计，因素水平见表 6 。采用“ 3.2 ”项下方法进行休止角模拟测定，结果见表 6 。

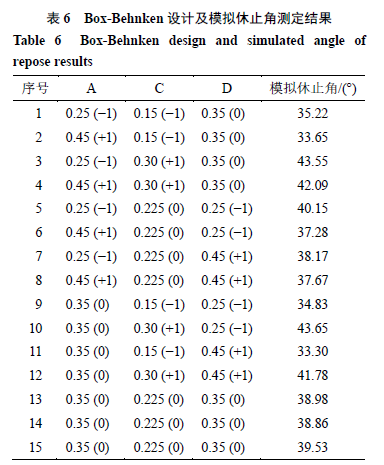
根据表 6 实验结果对自变量和响应变量进行全项 2 次多项式回归拟合，得到模型 1 ： α ＝ 26.22 － 9.88 A ＋ 76.42 C ＋ 12.19 D ＋ 3.73 AC ＋ 59.22 AD － 11.43 CD － 28.10 A ² － 37.67 C ² － 52.25 D ² 。模型方 差分析结果表明所得拟合模型 P ＜ 0.000 1 ，失拟项 P _L ＝ 0.482 5 ＞ 0.05 ，决定系数 R ² ＝ 0.995 4 ，表明回 归模型拟合良好。颗粒 - 颗粒恢复系数（ A ）、颗粒 - 颗粒滚动摩擦系数（ C ）、颗粒 - 不锈钢恢复系数（ D ）的 P 值均小于 0.01 ，对休止角的影响极其显著；颗粒 - 颗粒恢复系数颗粒 - 不锈钢恢复系数（ AD ）以及颗粒 - 不锈钢恢复系数的二次项（ D ² ） P 值 ＜ 0.05 ，对休止角的影响显著。将对休止角影响不显著（ P 值 ＞ 0.05 ）的项（ AC 、 CD 、 A ² 、 C ² ）移除，得到 优化的 2 次多项式回归模型，即模型 2 ： α ＝ 32.33 － 28.71 A ＋ 56.77 C ＋ 7.15 D ＋ 59.22 AD － 48.73 D ² 。模型 2 的 P ＜ 0.000 1 ，失拟项 P _L ＝ 0.575 3 ＞ 0.05 ，决定系数 R ² ＝ 0.992 5 ，表明优化后的模型仍具有良好的可靠性。响应值的范围为 33.30 ° ～ 43.64 ° ，该范围涵盖了表 1 中 4 种物料实验测定休止角，表明模型 2 可用于表 1 中 4 种物料的接触参数 A 、 C 和 D 的标定。

5.4 模拟参数优化和验证

以生甘草浸膏粉接触参数 A 、 C 和 D 的标定为例，以休止角试验测定值 41.18 °为目标，基于“ 5.3 ”项优化后的回归模型 2 ，应用 Design Expert 软件数值优化求解功能，得到生甘草浸膏粉的接触参数为颗粒