
Python部落(python.freelycode.com)组织翻译,禁止转载,欢迎转发。
逻辑回归是现在监督分类算法中比较流行的一种,一般用来解决二元分类问题。不过一直以来人们认为逻辑回归只能用来解决二元分类问题,当然,这是不对的,逻辑回归算法也能够用来解决多元分类问题。所以,在这篇文章中我们将会在python中用2种方法实现逻辑回归算法解决多元分类问题。
本文目录如下:
1、二元分类和多元分类的不同
1.1、二元分类问题介绍
1.2、多元分类问题介绍
2、多元逻辑回归介绍
3、玻璃分类问题数据集介绍
4、在python中实现多元逻辑回归
5、总结
1、二元分类和多元分类的不同
从名字中就可以看到二元分类和多元分类的不同,不过下面的例子将会让你对这两者有更深刻的认识。首先来看下二元分类。
二元分类:
1、根据邮件主题及内容判断是否是垃圾邮件
2、根据天气信息判断是晴天还是雨天
3、银行根据顾客信用判断是否给顾客贷款
多元分类:
1、给定物体维度信息判断物体形状
2、识别不同种类的车辆
3、根据颜色强度判断颜色类型
从上面的例子中想必你会理解二元分类和多元分类的不同,如果要是还不明白下面就详细的来解释下这二者的不同。
1.1、二元分类问题介绍
二元分类就是先用训练数据集得出一种分类算法,之后用训练过的分类器来预测给定特征的目标,不过最终的结果只能有两种可能。就像在上面的例子中,邮件要么是垃圾邮件要么不是。总而言之,二元分类就是从两种可能的结果中预测出一种最可能的结果。
1.2、多元分类问题介绍
和二元分类不一样的是,多元分类最终的可能结果不止有两种,即多于两种。就像上面预测物体形状的例子,最终物体形状可以是三角形,矩形,正方形或其它可能的形状,其它例子也一样。总之多元分类就是从多于2种可能的结果中预测出一种最可能的结果。
经过上面的比较,想必你应该理解二者的不同了吧!接下来,让我们看下多元逻辑回归。
2、多元逻辑回归介绍
多元逻辑回归是逻辑回归算法的衍生物,将逻辑回归算法应用到多元分类问题上就可以将其称为多元逻辑回归。和一般逻辑回归算法不同的是,多元逻辑回归不仅在分类任务上不同,更深入的它们使用的是不同的函数。
在逻辑回归中,根据输入特征就能计算出最终可能结果的函数是Sigmoid函数,随后的高可能预测结果来自逻辑回归分类器提供的预测结果分类。但是在多元逻辑回归中采用的是Softmax函数。在这里,我们不打算讨论这两种函数工作的细节,可以参看以前的文章。不过,在进一步深入阅读时,希望你花费点时间了解一下下面的概念:
1、逻辑回归算法在机器学习中是如何工作的
2、Softmax和Sigmoid函数
3、多元逻辑回归分类器在机器学习中是如何工作的
4、逻辑回归模型在python中的实现方式
希望你能清楚了解上面的概念,接下来就开始最精彩的部分:构建多元逻辑回归模型。下面有两种不同的方法;
1、使用python的scikit-learn包中的二元逻辑回归分类器
2、将scikit-learn中的逻辑回归分类器改成多元逻辑回归模型
3、玻璃分类问题数据集介绍
在这一节中将用多元逻辑回归算法根据不同玻璃的特性来对玻璃进行分类,判断出它是哪一种类型的玻璃。在看玻璃类型之前,先来看下鉴别玻璃的一些关键指标:

特性和目标信息
从上表中可以看到1个玻璃鉴别数据集包含10个特性,接下来详细看一下:
特性:
1、编号:1到214
2、RI:折射率
3、Na:钠(单位测量:相应氧化物中的质量百分数,以下都是如此)
4、Mg:镁
5、Al:铝
6、Si:硅
7、K:钾
8、Ca:钙
9、Ba:钡
10、Fe:铁
玻璃类型
在最终的目标中有7种不同类型的玻璃,下面是根据用途分类的:
1、建筑用浮法玻璃
2、建筑用非浮法玻璃
3、车用浮法玻璃
4、车用非浮法玻璃(数据库没有)
5、容器类
6、餐用类
7、吊顶灯用
4、在python中实现多元逻辑回归
我们将根据下面的流程来构建多元逻辑回归模型:
1、安装必要的python包
2、下载数据集
3、可视化数据集
4、将数据分为训练和测试两类
5、为多元分类构建逻辑回归
6、实现多元逻辑回归
7、比较结果准确性
首先先来导入必要的python包。
必要python包
下面是一些常用的python机器学习包,如果还没有安装的请尽快安装。
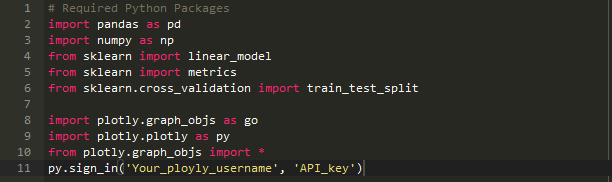
1、Pandas:一个数据分析包,本例中主要用来进行表格分析
2、NumPy:主要用来数值计算
3、Sklearn:是Python机器学习的算法工具包,主要有
3.1:linear_model:用来构建逻辑回归模型
3.2:metrics:用来计算训练的逻辑回归模型的准确性
3.3:train_test_split:用来将数据集分为训练和测试数据集
4、Plotly:将数据可视化
现在来下载数据集。
下载路径
可以从这个网址下载:
https://archive.ics.uci.edu/ml/datasets/Glass+Identification
或是从GitHub上克隆完整代码;
https://github.com/saimadhu-polamuri/DataAspirant_codes/tree/master/Multinomial_Logistic_regression

下载数据
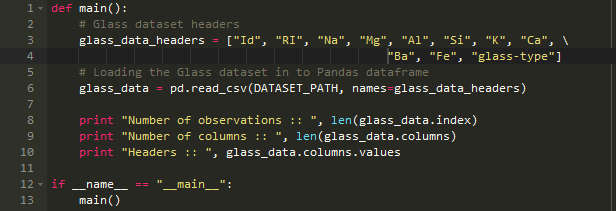
1、下载的数据没有标题,我们加个glass_data_headres标题
2、将数据传递到Pandas中的DataFrame去
3、打印出数据的列和标题
结果输出:

在用两种方法实施多元逻辑回归前,先来了解下数据。为了了解每个特性与玻璃类型的关系,我们首先创建个密度图,从密度图中可以观察到单个特性与玻璃类型之间的变化关系。不知道什么是密度图不要紧,接下来的实例将会展示。首先写个代码来创建密度图并将结果存在本地;
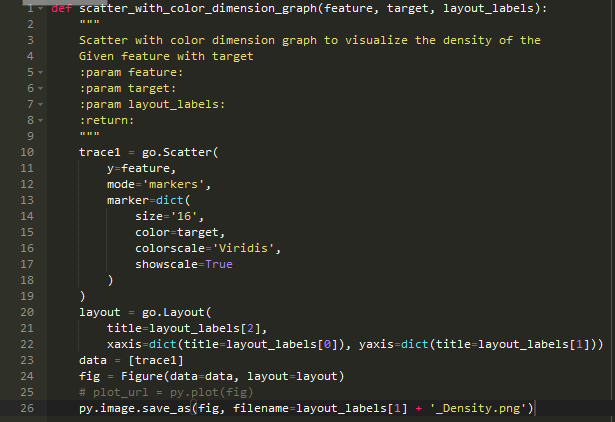
1、函数scatter_with_color_dimension_graph将会接受玻璃特性为输入参数,然后生成前面说的密度图
2、将生成的密度图保存在本地
3、上面的代码只是个画图的模板,可以用其它参数来作为输入得到不同的结果
现在用虚拟特征来调用这个函数:

结果输出:

1、glass_data_RI:这是玻璃折射率的特征值,结果只是前十个数据
2、glass_data_target:结果和不同玻璃类型之间的对应关系
现在将结果可视化:

调用函数scatter_with_color_dimension_graph得到下面的图:
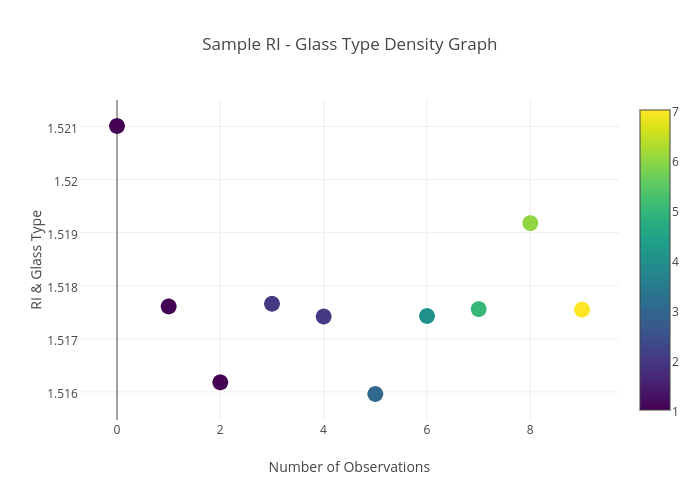
1、上图可以看出物体特性和目标之间的关系
2、黄色圆圈代表的为7号玻璃类型
3、右边栏可以知道对应的玻璃类型,左边是对应的特征值
4、如果绘制更多的观测图这个特征值将会归为类型7
现在来创建密度图以及其它特征的图:
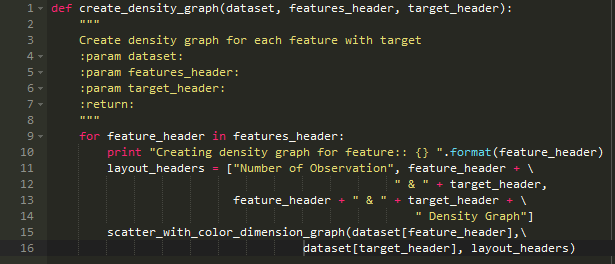
1、函数create_density_graph将会把features_header和target_headers作为输入参数
2、在函数内部认为features_header包含feature_header,并且调用函数scatter_with_clolor_dimenstion_graph.
现在将上述函数放在主函数里

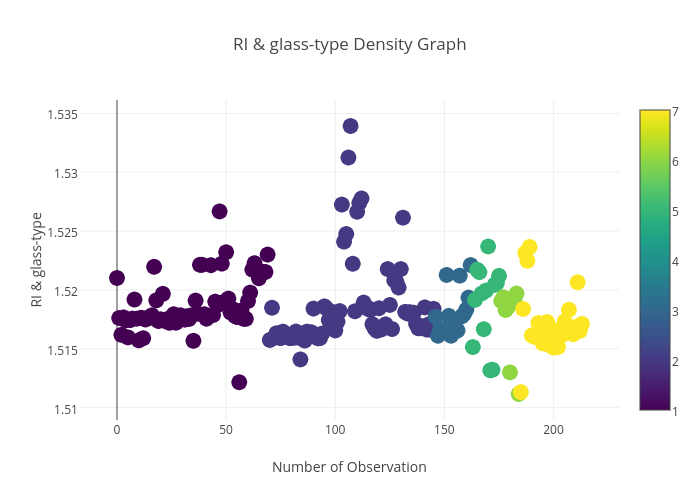
上面的代码将会画出下面的图形,每一个图形给出特性与玻璃种类之间的关系。
折射率与玻璃种类之间的关系:
Na与玻璃种类之间的关系:
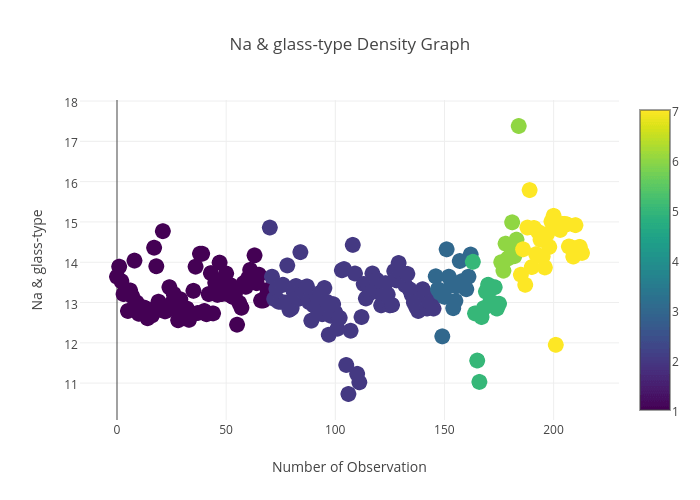
Mg与玻璃种类之间的关系:
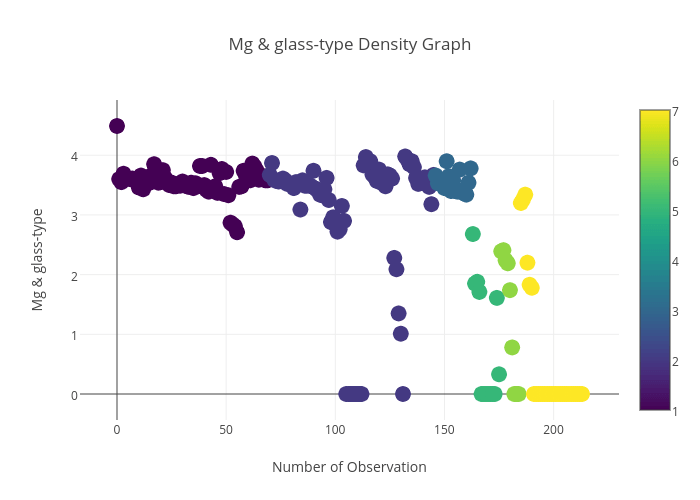
Al与玻璃种类之间的关系:

Si与玻璃种类之间的关系:

K与玻璃种类之间的关系:
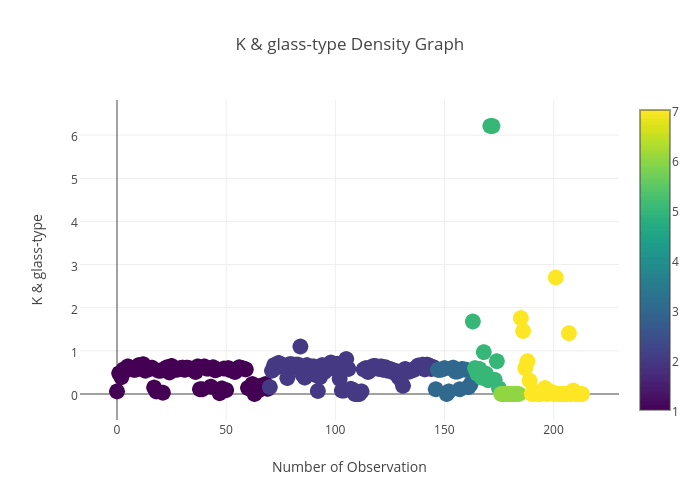
Ca与玻璃种类之间的关系:
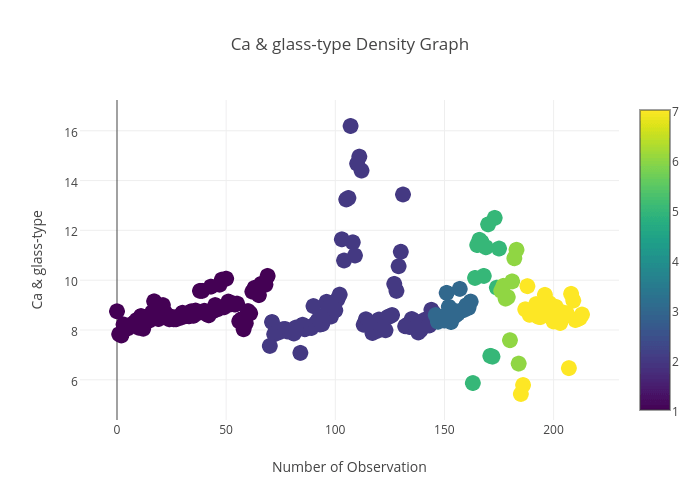
Ba与玻璃种类之间的关系:
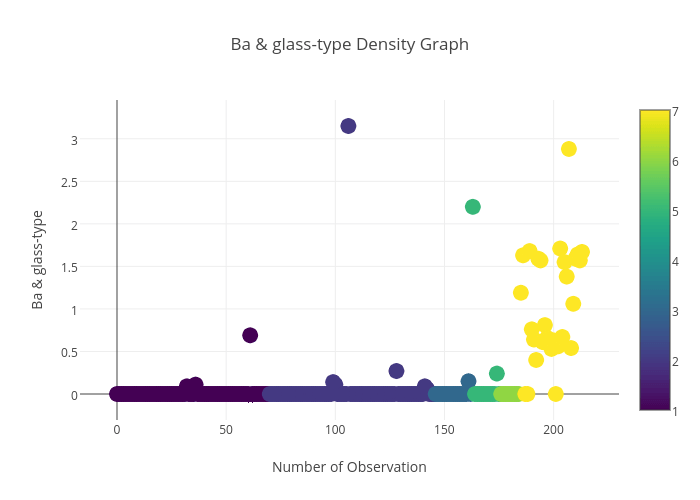
Fe与玻璃种类之间的关系:
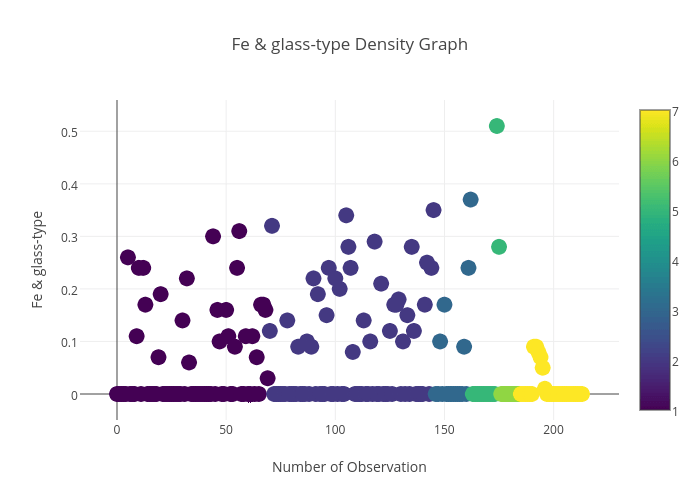
请花点时间仔细理解每幅图中特性与玻璃种类之间的关系,接下来我们将用这些特性来构建多元逻辑回归模型。为了构建多元逻辑回归模型,我用了玻璃分类的所有特征,当然你可以使用你认为最合适的特征来构建。训练多元数据模型需要特征与玻璃种类相匹配,为此,我将数据集分成四部分;
1、train_x
2、test_x
3、train_y
4、test_y
接下来,我们用train_x和train_y来构建多元逻辑回归模型,用tesst_x和test_y来计算模型的准确性。
将数据集分成训练和测试两部分
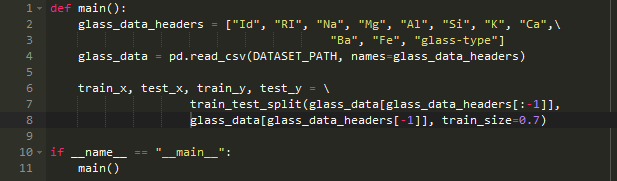
1、我们用scikit-learn中的train_test_spilt函数来划分玻璃数据集
2、随机将数据集中的70%划分为训练用,剩下的用来测试
为多元分类构建逻辑回归
在第一种方法中,我们用scikit-learn中的逻辑回归分类器来构建多元分类分类器

1、用scikit-learn中linear_model下的LogisticRegression函数来构建逻辑回归模型
2、接下来,将train_x和train_y作为玻璃分类中逻辑回归模型的训练数据
实验多元逻辑回归
在第二种方法中,在修正模型之前传入多元变量:
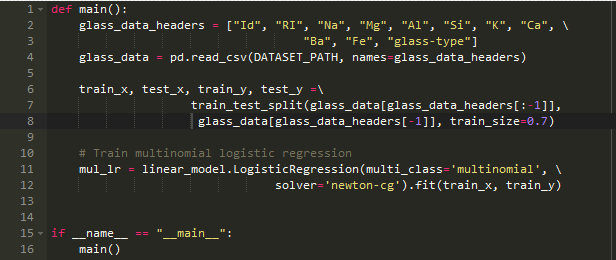
比较准确性
两个模型中都没有比较训练数据和测试数据的准确性
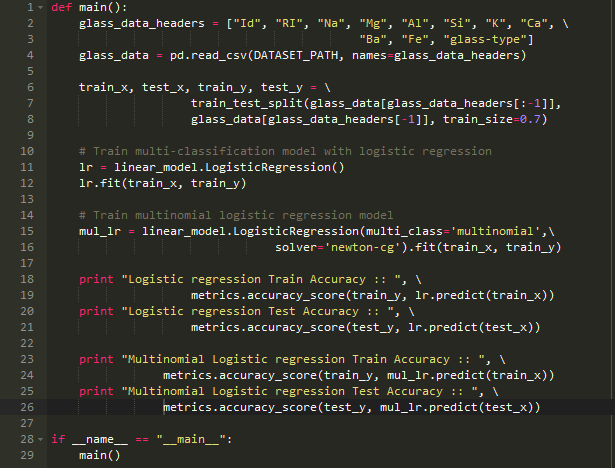
1、为了计算训练的多元逻辑回归模型的准确性,我们用scikit-learn中的metrics方法
2、在accuracy_score中的metrics方法来计算实际和预测结果的准确性
多元逻辑回归模型的准确性

从上面的结果中我们可以看到直接使用scikit-learn中的逻辑回归的准确性是比多元逻辑回归模型低的,现在可以使用这个代码了。
多元逻辑回归的完整代码

可以在这个地址下载完整的代码:
https://github.com/saimadhu-polamuri/DataAspirant_codes/tree/master/Multinomial_Logistic_regression
5、总结
读完这篇文章,你应该学会以下技能;
1、知道二元分类和多元分类的不同
2、明白多元逻辑回归的概念
3、最后,学会用pyhon的scikit-learn库以两种方法来构建多元逻辑回归模型
最后,如果有问题的话,欢迎在评论栏里留下你的评论。
英文原文:http://dataaspirant.com/2017/05/15/implement-multinomial-logistic-regression-python/
译者:Mr Chen















