
数学思维
数学之美
数学功底是什么?一言以蔽之,
数学的思维方式
。
数学的思维方式学得好,就算拿到一个新概念,也能快速理解并用来解决问题。就算不知道,只需要在遇到的时候现学就可以了。
那数学的思维方式有哪些呢?
▼▼▼
严格
这里说严格是区别于严谨。严谨更强调对细节的注意。而这里说的严格,就是
严格套定义
!定义说什么就是什么,不要掺入自己的想法!然后严格按定义严格判断和证明!
不要去想什么理不理解,定义就是那个样子,我经常很头疼的一个问题就是我不理解xx(概念),你给我讲一下。我直觉就是,有什么不理解的,定义就在那里,符合就对,不符合就错,没什么不理解的。
定义就在那里,非空集合,二元运算(从名字上就可以理解,二元就是两个元素,二元运算,显然就是两个元素参与的运算),封闭性,结合律,单位元,逆元的概念就在那里,清晰明了,没什么可以说的。然后问一个问题:实数对加法是否构成一个群?实数显然非空,加法也显然是一个二元运算。
来看定义。
(1)封闭性。对实数集中任意两个数a,b,a+b=c,c是唯一的吗,c也属于G吗?显然是肯定的,这条符合;
(2)结合律成立。任意(a+b)+c是否等于a+(b+c),太明显了,肯定成立;
(3)单位元存在。是否有某个实数e,使得实数a+e=e+a=a,什么数e加上一个另一个数会等于那个数本身呢,显然是0 ,单位元存在;
(4)逆元存在,任意一个数a ,是否存在b,使a+b=0呢,显然是对应的负数。成立
。
所以,实数集对加法构成群。
根据这个定义,也很容易判断,实数集对乘法不构成群。0不存在逆元。
这里用到了那些知识?除了
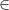 可能有人不认识,其他的都应该是一个初中生都能知道的。
可能有人不认识,其他的都应该是一个初中生都能知道的。
换句话说,给一个初中生看完群的概念,再让他判断实数集对加法能否构成一个群,都应该能判断出来!!
但是有多少初中生能独立判断出来?
严格按定义,看起来不值一提,但这是一种很深刻的数学素养,没见过的数学知识太多,如何在第一次遇到就迅速学习?就是严格看定义,不要去想什么理不理解。
▼▼▼
思想方法
其中最核心的是分析和综合。
综合
,就是从已知条件进行推导,看能得到什么东西。
分析
,就是从问题出发,看要解决问题,需要哪些东西。
一个综合的例子:对于一个非齐次线性方程组Ax=B,
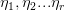 是其中r个解,记
是其中r个解,记
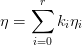 ,若
,若
 也是方程组的解,求
也是方程组的解,求
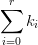 。
。
已知A*
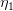 =B,A*
=B,A*
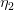 =B,A*
=B,A*
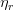 =B,
=B,
 也是解,那么A*
也是解,那么A*
 =B,
=B,
 是个什么呢?
是个什么呢?
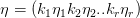 ,于是A
,于是A
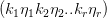 =B,
=B,
但是又注意到A*
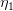 =B,A*
=B,A*
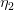 =B,A*
=B,A*
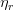 =B,于是
=B,于是
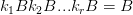
然后
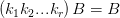 ,一目了然,
,一目了然,
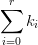
一个分析的例子:
我们现在将上一个例子改为证明
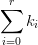 ,就是证明
,就是证明
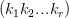 =1,为了证明这一串式子等于1,要是能证明
=1,为了证明这一串式子等于1,要是能证明
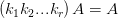 或
或
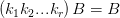 就好了。对于后面一个,一看,
就好了。对于后面一个,一看,
 ,于是
,于是
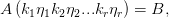
显然是成立的,就证明成功了。写过程的时候到去就可以了。这个例子可能不是很好⊙▽⊙只是为了说明从问题出发到已知条件的过程。
分析和综合多半是同时应用的,分析遇到难点就综合一下,然后继续推进。分析和综合的时候可能会得出一些没有用的推论,比如
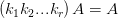 ,就不是很有用,用排除法,去掉没有用的就可以了。
,就不是很有用,用排除法,去掉没有用的就可以了。
▼▼▼
问题转化
对问题进行转化有两种很重要的思维方式:构造和映射。
构造就是构造一个函数、方程、新定义来解决和证明问题。
比如为了证明一个多项式比另一个大,构造一个差函数,用导数来证明差大于0。
映射就是将问题映射为一个模型或其他的东西,这个可能在科研里用得比较多。
图论里面也有很多例子。比如著名的七桥问题。
▼▼▼
多说几句
那么,数学功底究竟指的是什么?是建立模型解决问题的能力?是对纯数学的理解?是题海战术后会有的必然结果?还是只要认真思考,保持好奇心和求知欲后,对数学的那种不再惧怕,反而更加喜欢?
数学功底,如我开头所说,最本质是一种思维方式,但是这种思维方式一般要经过大量的练习和知识的积累才能形成。
我也是做了很多题之后才逐渐明晰这些想法。
平常看证明,看问题解析的时候的时候,不妨多想想,是如何来构造、对问题进行转化的,证明的结构是什么,先证明什么后证明什么。
有意识地培养上面提到的数学的思维方式,
抓定义,分析,综合,构造,映射
。
做题的时候也要有意识地运用分析综合的思想,想想从已知条件得到什么,哪些是有用的,哪些是没有用的。如果要构造一个东西来解决问题,应该怎么办…………多学习新知识。多接触新的领域,才能逐渐融会贯通。对知识有深入的理解,建立模型解决问题的能力才能逐渐增强。所谓以不变应万变。















