编者按:
长短时记忆网络(LSTM)是序列建模中被广泛使用的循环结构,LSTM利用门结构来控制模型中信息的传输量。但在实际操作中,LSTM中的门通常都处于“半开半关”的状态,没有有效地控制信息的记忆与遗忘。为此,微软亚洲研究院机器学习组提出了一种新的LSTM训练方法,让模型的门接近“二值化”——0或1,可以更准确地去除或者增加信息,进而提高模型的准确性、压缩比以及可解释性。
在很多实际场景中,深度学习模型都要面临
输入长度不固定或者说输入变长(variable-length input)
的问题:例如在文本判别中,我们需要判断一个句子的语义是积极还是消极的,这里输入句子的长度是多种多样的;在时间序列预测问题中,我们需要根据历史上信息的变化预测当前的数值,而历史信息的长度在不同时间点也是不同的。
普通的神经网络模型,比如卷积神经网络(CNN),无法解决此类输入变长的问题。为此,人们首先提出了循环神经网络(Recurrent Neural Network),简称RNN。
循环神经网络的核心是通过循环的方式,将历史信息和当前信息不断整合
。例如,当你看美剧第N集时,需要通过对前N-1集的剧情的理解(记忆),以及当前这一集的剧情(当前输入),更新自己对这部剧的理解。
在深度学习早期,RNN结构在很多应用中取得了成功,但同时,这个简单模型的瓶颈也不断显现,这不仅涉及到优化本身(如梯度爆炸、梯度消失)的问题,还有模型的复杂度的问题。例如一句话“小张已经吃过饭了,小李呢?”,这句话是在询问“小李是否吃过饭”,但在RNN看来,信息是从左到右不断流入的,所以最后很难分清到底是在问小张是否过饭,还是在问小李是否吃过饭。于是带有遗忘机制的新结构就诞生了——
长短时记忆网络(Long Short Term Memory Network,LSTM)
。
LSTM是由
Hochreiter & Schmidhuber在1997年
提出的RNN的一种特殊类型,可以学习长期依赖(long-term dependency)信息。在很多自然语言处理问题以及增强学习问题中,LSTM都取得相当巨大的成功,并得到了广泛的使用。
LSTM的关键构成是一种被称作“门”的结构,
LSTM通过精心设计的门结构去除或者增加信息
。门是一种让信息选择通过的方法。一般情况下,在一个维度上,一个门是一个输出范围在0到1之间的数值,用来描述这个维度上的信息有多少量可以通过这个门——0代表“不许任何量通过”,1代表“全部通过”。
LSTM拥有三类门,分别是
输入门、输出门、和遗忘门
。
首先,LSTM需要通过遗忘门决定应该从历史中丢弃什么信息。在每一维度,遗忘门会读取历史信息和当前信息,输出一个在0到1之间的数值,1表示该维度所携带的历史信息“完全保留”,0表示该维度所携带的历史信息“完全舍弃”。例如在前面的例子中,当我们读到“小张已经吃过饭了,小李呢?”时,我们会把“主语”信息中的小张忘掉,这个操作就是通过遗忘门实现的。
然后,要确定需要把什么新信息存放在当前内容中,例如前面的例子中,我们把小张“忘掉”后,需要把主语信息换成小李,这个“增加”操作是通过输入门实现的。而对于不同任务而言,我们需要将当前信息整理输出以方便做决策,这个整理输出信息的过程,是通过输出门实现的。LSTM如下图右所示。
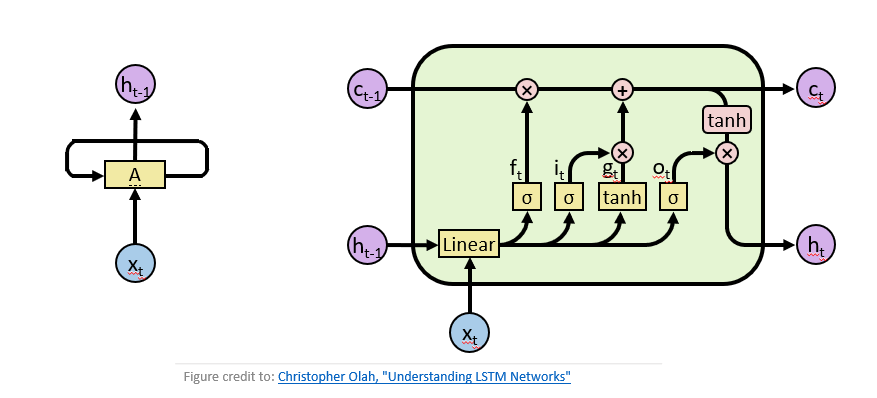
图1 左:经典循环神经网络,右:长短时记忆网络
在实际操作中,门是通过激活函数实现的:给定一个输入值x,通过sigmoid变换,可以的到一个值域在[0,1]之间的值,若x大于0,则输出值大于0.5,若x小于0,则输出值小于0.5。
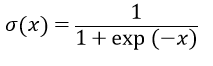
门是否真的具有我们上述描述的意义呢?这也是我们这篇论文的出发点。为了探究这个问题,我们分析了IWSLT14德语-英语的翻译任务,这个翻译任务的模型是基于LSTM的端到端(sequence-to-sequence)结构。
我们在训练集中随机抽取10000对平行语料,画出在这些语料上LSTM输入门与遗忘门的取值分布直方图,如下图所示。
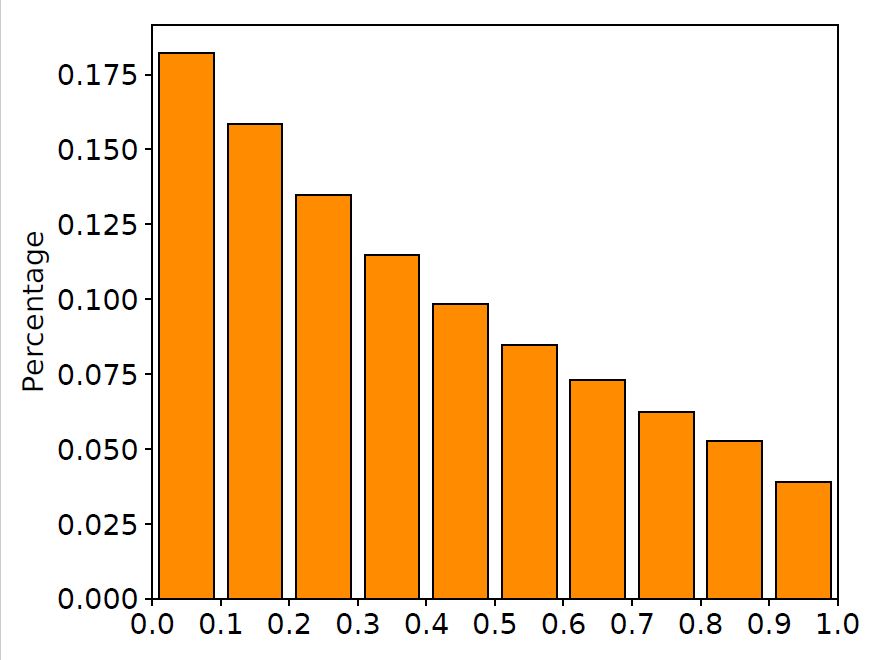
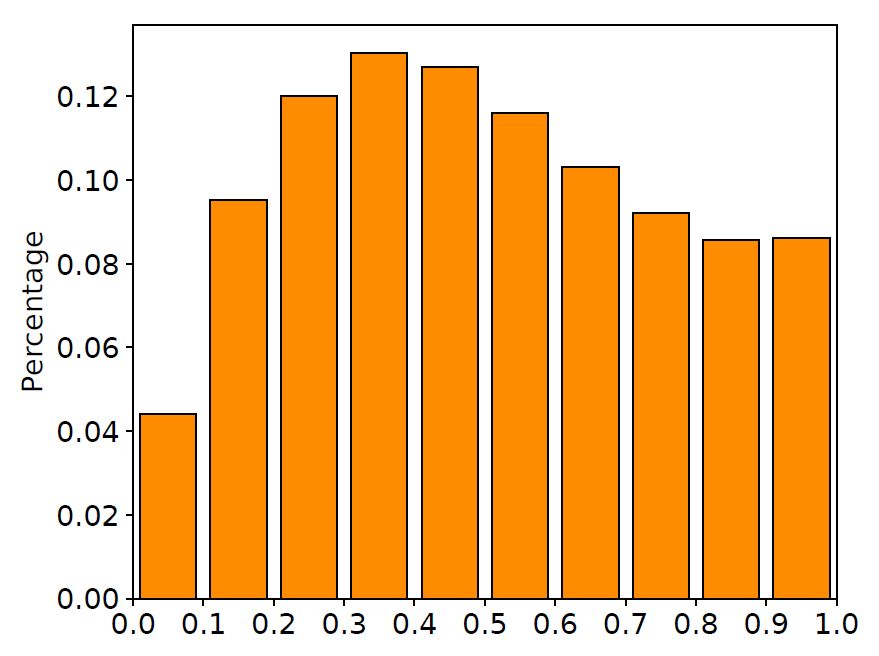
图2 输入门与遗忘门取值分布
从图中可以清晰地看到,很大一部分门的取值都在0.5附近。换句话说,
LSTM中的门都处于一种模棱两可的“半开半关”的状态
。这种现象与LSTM网络的设计有所出入:这些门并没有显式地控制信息的记忆与遗忘,而是以某种方式“记住”了所有的信息。与此同时,许多工作也指出LSTM中的大部分门都很难找到实际意义,这也进一步印证了我们的发现(相关讨论详见文末论文)。
从上面的例子中可以看到,虽然LSTM在翻译任务中取得了很好的效果,但是门并没有想象中的明显作用。同时也有一些前人的工作指出:LSTM的绝大多数维度并没有明显的可解释信息。那么如何能够学到一个更好的LSTM呢?这个问题引领我们去挖掘门结构更大的价值:既然门是一个开关的概念,那么有没有可能学习出一个接近“二值化”(binary-valued)的LSTM呢?一个接近“二值化”的门(binary-valued gate)有以下几点好处:
1
.
门的作用更加符合真实意义下门的概念:
通常意义下,门其实更多的是指其“开”、“关”两种状态。而我们去学习一个接近“二值化”的门的目的,也与LSTM的核心思想非常一致。
2
. “二值化”更适合模型压缩:
如果门的值非常接近0或者1,说明sigmoid函数的输入值x是个很大的正数,或者很小的负数。这时输入值x的微小改变对输出值影响甚微,由于输入值x通常也是参数化的,所以“二值化”可以方便对于这部分参数的压缩。通过实验我们发现,即使达到很大的压缩比,我们的模型仍然有很好的效果。
3
. “二值化”带来更好的可解释性
:要求门的输出值接近0或1,会对模型本身有更高的要求。在信息取舍的过程中,某个节点保留或者遗忘掉该维度全部信息。我们认为这种学习得到的门更能体现自然语言的结构、内容以及内部逻辑,如前面提到的关于吃饭的例子。
如何让训练后的模型的门接近二值化?我们借鉴了ICLR17上关于变分法(variantional method)的一个新进展:Categorical Reparameterization with Gumbel-Softmax。简单而言,将门的输出“二值化”的最好办法是训练一个随机神经网络(stochastic neural network),其中门的输出是一个概率p,在伯努利分布中得到0/1的随机采样,借此去得到不同位置取0/1时的损失,进而优化参数得到最优p。而在隐层节点上进行离散操作时,梯度回传遇到问题,我们采用的方法就是用Gumbel-Softmax Estimator近似多项分布的概率密度函数,进而达到既可学习又方便优化的目的(具体方法见文末论文)。我们将这一方法命名为Gumbel-Gate LSTM,简称G
2
-LSTM。
我们在
LSTM
网络的两个经典应用——语言模型和机器翻译上测试了这一方法,在准确率、可压缩性与可解释性三方面与之前的
LSTM
模型进行比较。
准确率
语言模型是
LSTM
网络最基本的应用之一。语言模型要求
LSTM
网络根据一句话当中之前已知的词语准确预测下一个词的选取。我们使用广泛使用的
Penn Treebank
数据集作为训练语料,该训练集总共包含约一百万个词。语言模型一般使用
perplexity
作为评价指标,
perplexity
越小说明模型越精准,实验结果如下图所示。
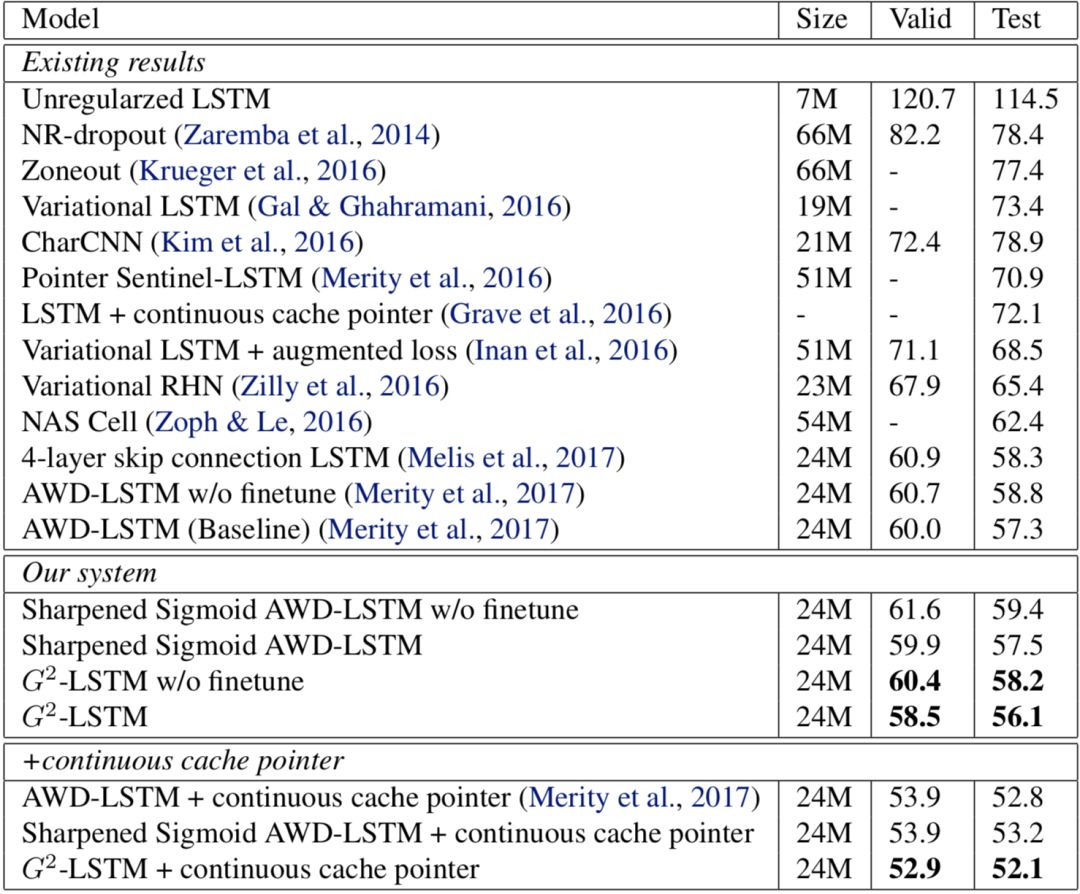
图
3
语言模型实验结果
从图中可以看到,通过将
LSTM
中的门进行“二值化”,模型的表现有所提升:我们模型的
perplexity
为
56.1
,与基线模型的
perplexity57.3
相比,有
1.2
的提升。而在加入了测试时后处理(
continuous cache pointer
)的情况下,我们的模型达到了
52.1
,较基线模型的
52.8
有
0.7
的提升。
机器翻译是目前深度学习应用最为成功的领域之一,而基于
LSTM
的端到端(
sequence-to-sequence
)结构是机器翻译中被广泛应用的结构。我们在两个公开数据集:
IWSLT14
德语到英语数据集和
WMT14
英语到德语数据集上测试了我们的方法。
IWSLT14
德英数据集包含约
15
万句平行语料,
WMT14
英德数据集包含约
450
万句平行语料。对于
IWSLT14
德英数据集,我们使用了两层编码器
-
解码器(
encoder-decoder
)结构;而由于
WMT14
英德数据集大小更大,我们使用了更大的三层编码器
-
解码器结构。机器翻译任务一般由测试集上的
BLEU
值作为最后的评价标准,
BLEU
值越高说明翻译质量越高,机器翻译的实验结果下图所示。

图
4
机器翻译实验结果
与语言模型的实验结论类似,我们的模型在机器翻译上的表现同样有所提升:在
IWSLT14
德英数据集上,我们模型的
BLEU
值达到了
31.95
,比基线模型高
0.95
;而在
WMT14
德英数据集上,我们模型的
BLEU
值为
22.43
,比基线模型高
0.54
。
可压缩性
将模型进行“二值化”能够使得我们的模型对于参数的扰动更加鲁棒。因此,我们比较了不同模型在参数压缩下的性能。我们采用了两种方式对与门相关的参数进行压缩:
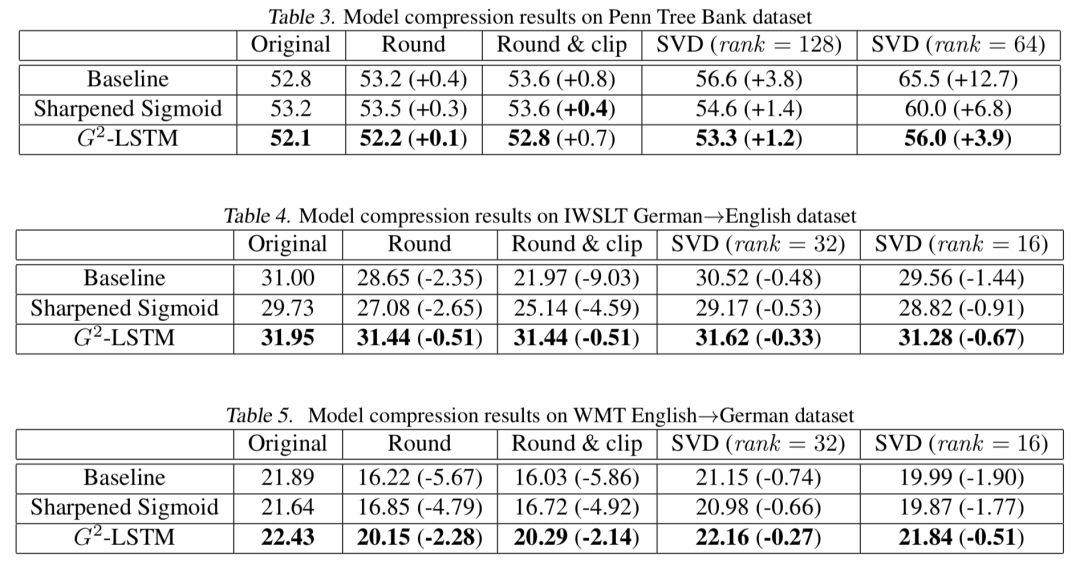
图
5
压缩后实验结果
具体的实验结果如上图所示。我们可以看到,不论在哪种情况下,我们的模型都显著优于压缩后的模型,这说明这一模型的鲁棒性较之前的
LSTM
有大幅度的提升。
可解释性
除了比较数值实验结果外,我们进一步地观察了模型中门的取值,用同样的语料画出了我们的模型中门的取值分布直方图,如下图所示。

















