现在的深度学习发展似乎已经陷入了大型化、深度化的怪圈，我们设计的模型容易被对抗样本欺骗，同时又需要大量的训练数据——在无监督学习上我们取得的突破还很少。作为反向传播这一深度学习核心技术的提出者之一，Geoffrey Hinton 很早就意识到反向传播并不是自然界生物大脑中存在的机制。那么，在技术上，反向传播还有哪些值得怀疑的地方？
反向传播的可疑之处
Geoffrey Hinton 对人工智能的未来非常担忧。在最近的一次人工智能会议上，Hinton 表示自己对于反向传播「非常怀疑」，并提出「应该抛弃它并重新开始」。
在人工智能多年的发展过程中，反向传播已经成为了深度学习不可或缺的一部分。研究人员发现，只要层是可微分的，我们就可以在求解时使用任何计算层。换句话说，层的梯度是可以被计算的。更为清楚地说，在寻物游戏中，准确表现出被蒙住眼睛的玩家与他的目标之间的距离。
在反向传播上，存在着几个问题：第一个是计算出来的梯度是否真的是学习的正确方向。这在直观上是可疑的。人们总是可以寻找到某些看起来可行的方向，但这并不总是意味着它最终通向问题的解。所以，忽略梯度或许也可以让我们找到解决方案（当然，我们也不能永远忽略梯度）。适应性方法和优化方法之间存在着很多不同。
现在，让我们回顾一下反向传播思想的起源。历史上，机器学习起源于曲线拟合的整体思路。在线性回归的具体情况下（如对一条线进行拟合预测），计算梯度是求解最小二乘问题。在优化领域，除了使用梯度找到最优解之外，还有许多其他方法。不过，事实上，随机梯度下降可能是最基本的优化方法之一。所以它只是我们能想到的很多方法中最为简单的一个，虽然也非常好用。
大多数研究优化的学者很长一段时间以来都认为深度学习的高维空间需要非凸解，因此非常难以优化。但是，由于一些难以解释的原因。深度学习使用随机梯度下降（SGD）的效果却非常好。许多研究人员对于为什么深度学习用 SGD 优化如此简单提出了不同解释，其中最具说服力的说法是这种方法倾向于找到真正的鞍点——而不是小范围内的谷地。使用这种方法的情况下，总是有足够的维度让我们找到最优解。
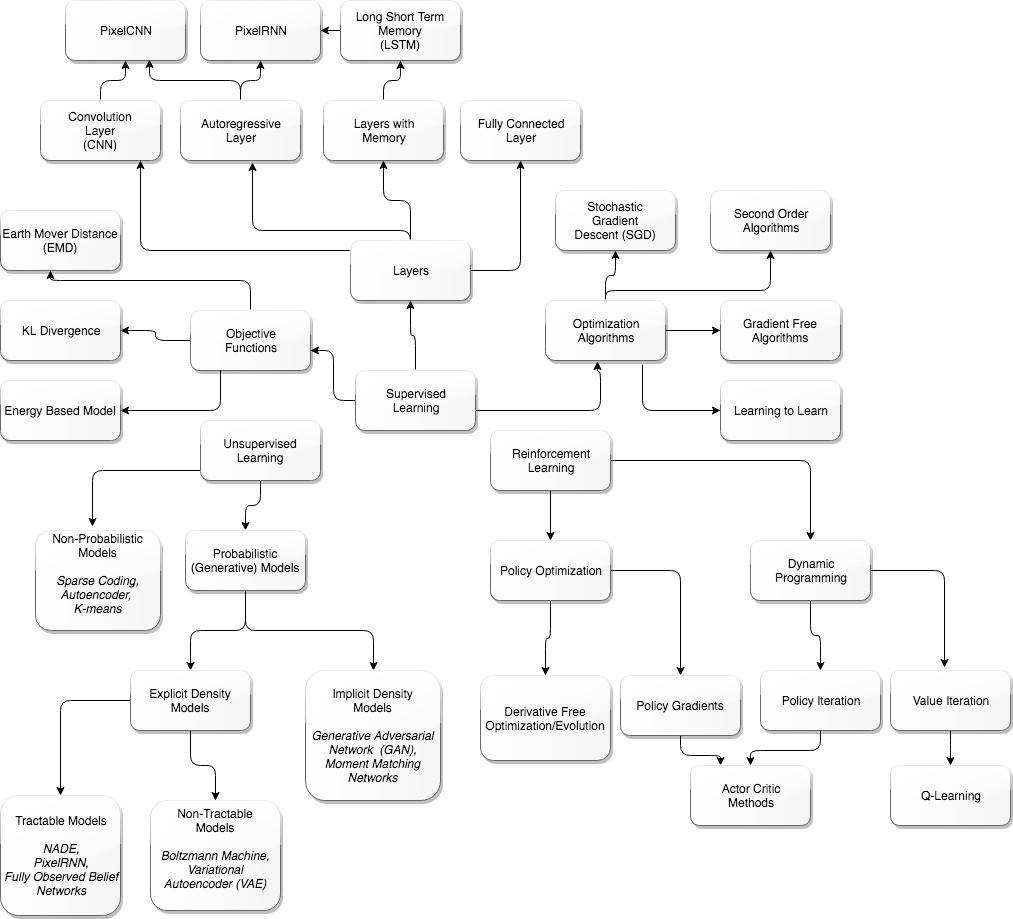
一张指导图，防止迷失
DeepMind 研究的合成梯度是一种解耦层方法，以便于我们不总是需要反向传播，或者梯度计算可推迟。这种方法同样非常有效。这一发现可能也是一种暗示，正在产生更通用的方法。好像关于这个方向的任何升级都是有益的（随意提了一下合成梯度），不管效果是不是一样。
还有一个使用目标函数的典型问题：反向传播是相对于目标函数计算的。通常，目标函数是预测分布与实际分布之间差异的量度。通常，它是从 Kullback-Liebler 散度衍生出来的，或者是像 Wassertsein 这样的其他相似性分布数值。但是，在这些相似性计算中，「标签」是监督训练必不可少的一部分。在 Hinton 抛出反向传播言论的同时，他也对于监督学习发表了自己的看法：「我认为这意味着放弃反向传播……我们确实不需要所有数据都有标签。」
简而言之，没有目标函数就无法进行反向传播。如果你无法评估预测值和标签（实际或训练数据）的 value 值，你就没有目标函数。因此，为了实现「无监督学习」，你需要抛弃计算梯度的能力。
但是，在我们把这一重要能力丢掉之前，先从更通用的角度看一下目标函数的目的。目标函数是对自动化内部模型预测所处环境的准确率的评估。任何智能自动化的目的都是构建准确率高的内部模型。但是，模型和它一直或持续所处的环境之间不需要任何评估。也就是说，自动化不需要执行反向传播进行学习。自动化可以通过其他途径改善其内部模型。
其他途径就是「想象力」（imagination）或「做梦」（dreaming），不用立刻把预测与事实对比然后更新参数。今天最接近的体现就是生成对抗网络（GAN）。GAN 包括两个网络：生成器和鉴别器。你可以把鉴别器当作使用目标函数的神经网络，即它可以用现实验证内部生成器网络。生成器自动化创造近似现实。GAN 网络使用反向传播，执行无监督学习。因此，无监督学习可能不需要目标函数，但它或许仍然需要反向传播。
看待无监督学习的另一种方式是，某种程度上，它是一种元学习。系统不需要监督训练数据的一种可能原因是学习算法已经开发出自己的最佳内部模型。也就是说，仍然存在一定程度的监督，只不过在学习算法中更加隐晦。学习算法如何具备这种能力尚不可知。
总之，现在判断我们是否可以抛弃反向传播还为时尚早。我们当然可以使用没有那么严格的反向传播（即合成梯度或其他启发）。但是，逐步学习（或称爬山法）仍然是必要的。我当然对找到驳斥逐步学习或爬山法的研究很感兴趣。这实际上可以类比为宇宙的运行，具体来说就是热力学的第二定律。再具体点就是熵一直在提高。信息引擎将降低熵，以交换所处环境中的熵提高。因此，没有一种方法可以完全避免梯度，除非存在「永动信息机器」（perpetual motion information machine）。
Hinton 与他的谷歌同事 Sara Sabour 和 Nicholas Frosst 共同完成的论文《Dynamic Routing Between Capsules》已被 NIPS 2017 大会接收，他们在研究中提出的 capsule 概念正是 Hinton 对于未来人工智能形态的探索。不可否认的是，在无监督学习的道路上，我们还有很长的一段路要走。
反向传播的推导过程
神经网络在权重的变化和目标函数的变化之间不再是线性关系。在特定层级的任何扰动（perturbation）将会在连续层级中进一步变化。那么，我们该如何计算神经网络中所有权重的梯度，从而进一步使用梯度下降法（最速下降法）呢？这也就是我们为什么要使用反向传播算法的地方。反向传播算法的核心即对整个网络所有可能的路径重复使用链式法则。反向传播算法真正强大的地方在于它是动态规划的，我们可以重复使用中间结果计算梯度下降。因为它是通过神经网络由后向前传播误差，并优化每一个神经节点之间的权重，所以这种算法就称之为反向传播算法（backpropagation algorithm）。实际上神经网络反向传播与前向传播有紧密的联系，只不过反向传播算法不是通过神经网络由前向后传播数据，而是由后向前传播误差。
大多数反向传播算法的解释都是直接从一般理论推导开始，但是如果从手动计算梯度开始，那么就能很自然地推导出反向传播算法本身。虽然下面的推导部分较长，但我们认为从数学基本理论开始是最好的方式来了解反向传播算法。
下文由单路径神经网络开始，进而推广到存在多层和多个神经元的神经网络，最后再推导出一般的反向传播算法。
反向传播算法的基本原则
我们训练神经网络的最终目标是寻找损失函数关于每一个权重的梯度：
当我们计算出偏导数时就能进一步使用随机梯度下降或小批量梯度下降更新每一层神经网络的权重：
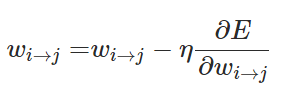
通常在一般神经网络的每一个单元会存在以下几种情况：
该神经元有且仅有一个输入和一个输出
该神经元有多个输入
该神经元有多个输出
该神经元有多个输入和输出
因为多输入与多输出是独立的，我们能自由组合输入与输出神经元的数量。
这一部分将从相对简单的结构到多层神经网络，并在这个过程中推导出用于反向传播的一般规则。最后，我们会将这些规则组合成可用于任意神经网络的反向传播算法。
单一输入与单一输出的神经元
在上面的神经网络中，每一个变量都能够准确地写出来。
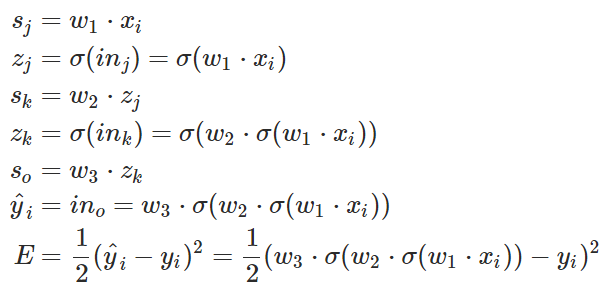
注意，上面方程式中 x 是输入，w 是权重，Sigamm 是神经元的激活函数。s 是前一个神经元通过权重传递到后一个神经元的数据，它等于前一个神经元的输出乘以两个神经元的连接强度，即权重 w。z 是神经元输入经过激活函数 Sigamma 计算后得到的输出。
对于这样一个简单的案例来说，我们很容易就找到其偏导数项。现在我们将求导后的一部分标以蓝色，然后看看我们是否能推导出可以在迭代算法中使用的模式。首先我们需要了解 k 层到 o 层之间的权重（w_k→o），也可以理解成这两个神经元之间的连接强度。如果我们的输出是线性单元，那么（
）：
E 就相当于系统做出的判断与正确标注之间的损失。E 对权重 w 求偏导并最小化，即在损失函数 E 最小的情况下求得权重 w，上述方程式表明需要求得 k 神经元到 o 神经元之间最优权重 w。
那么从 j 到 k 和从 i 到 j 的权重更新都是相同的步骤了。
上面的推导表达式展示了损失函数对第 j 层和第 k 层之间权重的偏导数，而下面的推导表达式则展示了损失函数对第 i 层和第 j 层之间权重的偏导数：
现在也许我们能总结一个可以使用反向传播算法的权重更新模式。当我们计算神经网络前面层级的权重更新时，我们重复使用了多个数值。具体来说，我们观察到的就是神经网络损失函数的偏导数，上面三个推导表达式可以总结为：
在上述方程式中由后一个神经元向前推导，最后一层的权重更新梯度最简单，而前面层级的更新梯度则需要向前推导，这一推导的过程或者方式就是根据求导的链式法则。
多个输入
可以思考一下稍微复杂一点的神经网络，即一个神经元将有多个输入：
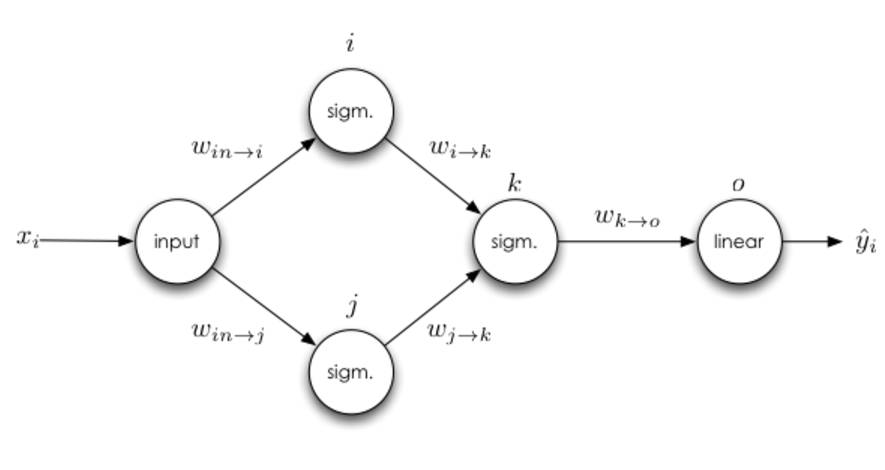
如果一个神经元有多个输入端怎么办，从 j 到 k 的权重更新规则会不会影响从 i 到 k 的权重更新规则？为了弄清这个问题，我们可以对 i 到 k 的权重手动求导。
我们可以从上面看到从 i 到 k 的权重更新是不依赖于从 j 到 k 权重的导数的，因此第一条准测就是损失函数对权重的导数不依赖于同层级神经网络上的其他任何权重的导数，所以神经网络同层级的权重可以独立地更新。同时该法则还存在更新的自然顺序，这种自然顺序仅仅只依赖于神经网络同一层级其他权重的值，这种排序是反向传播算法的计算基础。
多个输出
接下来我们可以思考下有多个输出的隐藏层神经元。
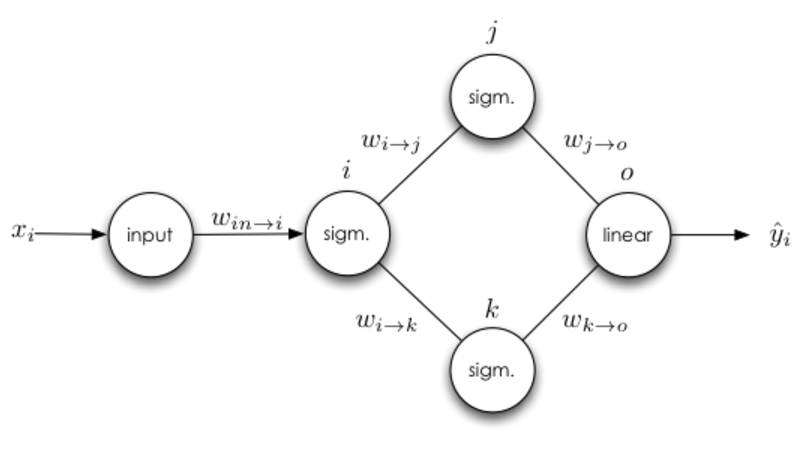
在前面的基础上，唯一和前面权重更新有差别的是输入神经元与 i 神经元之间的求导法则。神经元多输出端的情况就是其有多个直接后继神经元，所以我们必须沿着以神经元 i 为根结点的所有路径来计算误差的总和。接下来我们可以详细地写出损失函数对权重求导而更新的过程，并且我们定义σ(⋅) 就是神经元 i 的激活函数：
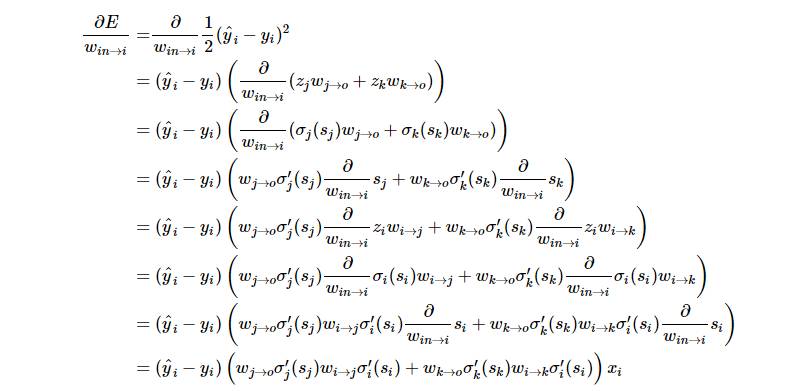
现在有两点需要注意，首先就是第二条推导准则：具有多个输出的神经元权重更新依赖于所有可能路径上的导数。
但是更重要地是我们需要看到反向传播算法和正向传播算法之间的联系。在反向传播的过程中，我们会计算神经网络输出端的误差，我们会把这些误差反向传播并且沿着每条路径加权。当我们传播到了一个神经元，可以将经权重反向传播过来的误差乘以神经元的导数，然后就可以同样的方式反向传播误差，一直追溯到输入端。反向传播非常类似于正向传播，是一种递归算法。接下来会介绍误差信号，然后再改写我们的表达式。
误差信号
手动求出所有权重的更新是十分棘手的，特别是在有上百神经元和多层神经网络的情况下。但是我们在最后的几部分看到一种模式，即误差是沿着神经网络向前传播的。因此我们可以定义误差信号为每一个神经元的累积误差，即使用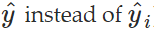
我们定义神经元 j 的迭代误差信号为：
其衡量了随着数据输入到神经元 j，神经网络的误差改变了多少。使用误差信号有很好的性能，也就是我们可以用更紧凑的形式来表达反向传播。为了理解这之间的变化，我们可以展开方程式。
如果神经元 j 是一个输出节点，这也就意味着
(如果神经元 j 的激活函数是 f_j(⋅)），所以
就可以简单地写为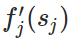
，因此就可以求出
。
另外，如果神经元 j 是一个隐藏神经元，那么另一层的神经元 k 属于 j 的输出神经元。我们可以使用链式求导法则进一步解释
：
注意最后的偏导项 ∂y^ /∂zj，多神经元取决于 z_j，确切的说是所有 k∈outs（j）的神经元。我们在多个输出端的部分中看到，导致具有多个输出神经元的权重确实对这些输出神经元有影响。但对于每个神经元 k，我们有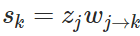
，每个 s_k 不取决于任何其它同层的结点。因此，我们可以再次使用链式规则并对 k∈out（j）的输出结点求和：
将这个方程式带入
，我们就能得到：
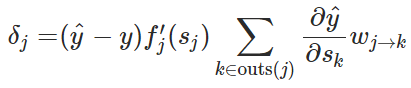
基于我们对误差信号的定义，我们已经知道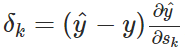
，所以如果我们 (y^−y) 放入求和中，我们就能得到以下递归关系：
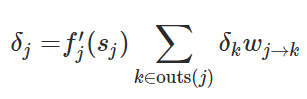
现在我们能用紧凑的方程式表征反向传播误差。
反向传播算法的普遍形式
先回忆下第一部分的简单神经网络:
我们能使用 δ_i 的定义导出整个神经网络的所有误差信号：
在这一个神经网络中，准确的权重更新模式是以下方程式：
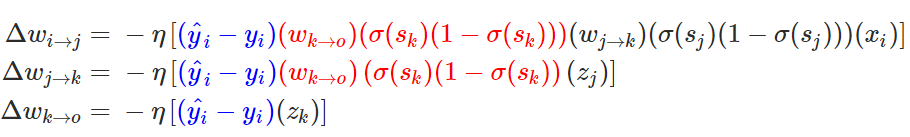
如果使用误差信号代替，我们可以得到以下形式：
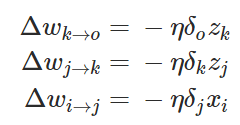
还有另外一个复杂一点的神经网络，即有多个输出神经元：
同样我们能得出所有的误差信号：
然后我们再一次将误差代入到权重更新方程式中：
现在也许我们就可以推导出权重更新的简单通用形式：
最后我们需要考虑的是我们要不要使用小批量梯度下降。因为我们将每一个 y_i 都看成独立的，所以我们可以将所有训练样本求和来计算完整的权重更新。对每一个独立的训练样本 y_i，我们加上一个上标表示（y_i）表示随每一个训练样本而改变的参数值，因此通用的更新形式可以写为：
最后，反向传播算法更新权重的一般形式可以表示为以下几个步骤：
1. 将训练样本沿整个网络前向传播，并且记录每一个
。
2. 对于所有的神经元 j 和每一个训练样本 y_i 计算误差信号
，如果 j 是输出神经元，那么有：
如果 j 不是输出神经元，那么有：
3. 通过以下更新法则更新权重：
上面是一般反向传播算法的推导和建立过程，我们从最简单与直觉的概念一步步完善并推导出最后的更新规则。虽然反向传播算法有着很多的局限性与不足，并且也有学者提出如解耦方法等理论解决反向传播算法的不足，但反向传播算法仍然是目前神经网络中最主流与强大的最优化方法。最后我们同样期待 Hinton 等人所提出的capsule能对反向传播算法有本质上的提升！
原文链接：
本文为机器之心编译，转载请联系本公众号获得授权。
✄------------------------------------------------
加入机器之心（全职记者/实习生）：[email protected]
投稿或寻求报道：[email protected]
广告&商务合作：[email protected]
