长按二维码进哲园书屋
相关知识
连续统
连续统是一个数学概念。当人们笼统地说：“在实数集里实数可以连续变动”，也就可以说实数集是个连续统；更严格的描述需要使用序理论、拓扑学等数学工具。这里的连续是相对于离散的概念而言的。在不讨论精确的定义前，有时人们也会谈到一个量可以在某范围内连续取值，或者说该量的变化范围是一个连续统。在数学上，连续统这一术语至少有两种精确定义，但并不等价。另外，连续统一词有时即指实数线或者实数集，这是较旧的叫法；见连续统假设。
目录
1 有序集
1.1 连续统的基数
2 拓扑学
有序集
在集合论中，连续统是一个拥有多于一个元素的线性序集，而且其序满足如下性质（具此性质的序称为“稠密无洞”的）：
稠密：在任意两个元素之间存在第三个元素
无洞：有上界的非空子集一定有上确界
实数集即为连续统的例子；实际上它是连续统的原型。以下是连续统的几个例子：
序结构与实数集同构（序同构）的集合，例如实数集里的任何开区间
扩展的实数轴，以及序同构于它的，比如单位区间。
实的半开半闭区间如 (0,1] 等，以及其序同构。
拓扑学中有一种比实数线还要长的“长线”（en:long_line）
非标准分析中的超实数集
连续统的基数
主条目：连续统的势
康托的连续统假设有时会被叙述成“在连续统的基数和自然数的基数之间不存在任何基数”，这里的“连续统”指的是实数集；连续统的基数即特指实数集的基数。
拓扑学
在点集拓扑学中，一个连续统是指任何非空的紧致连通度量空间（或者非空的紧致连通豪斯多夫空间，但较少用）。
按照以上定义，一个单点集也是连续统。拥有多于一个点的连续统称为非退化的连续统；由连通性和豪斯多夫性质，可知它一定含有无穷个点。连续统理论即是拓扑学中研究拓扑连续统的分支。其中一个有趣的问题是不可分解连续统的存在性：
是否存在这样的连续统 C ，它可以写成两个连续统的并集，且这两个都是 C 的真子集？
答案是肯定的，第一个例子由鲁伊兹·布劳威尔给出[1]。
连续统假设
在数学中，连续统假设（德语：Kontinuumshypothese；英语：Continuum hypothesis，简称CH）是一个猜想，也是希尔伯特的23个问题的第一题，由康托尔提出，关于无穷集的可能大小。其为：
不存在一个基数绝对大于可列集而绝对小于实数集的集合。
康托尔引入了基数的概念以比较无穷集间的大小，也证明了整数集的基数绝对小于实集的基数。康托尔也就给出了连续统假设，就是说，在无限集中，比自然数集{0，1，2，3，4......}基数大的集合中，基数最小的集合是实数集。而连续统就是实数集的一个旧称。
更加形式地说，自然数集的基数为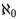
（读作“阿列夫零”）。而连续统假设的观点认为实数集的基数为
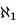（读作“阿列夫壹”）。于是，康托尔定义了绝对无限。
等价地，整数集的基数是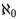而实数的基数是
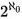，连续统假设指出不存在一个集合 S使得
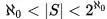，假设选择公理是对的，那就会有一个最小的基数
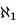大于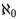，而连续统假设也就等价于以下的等式：
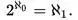
连续统假设有个更广义的形式，叫作广义连续统假设（GCH），其命题为：
对于所有的序数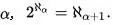
库尔特·哥德尔在1940年用内模型法证明了连续统假设与ZFC的相对协调性（无法以ZFC证明为误），保罗·柯恩在1963年用力迫法证明了连续统假设不能由ZFC推导。也就是说连续统假设独立于ZFC。
目录
1 作为希尔伯特第一问题
2 集合的大小
3 证明或证否的不可能性（在ZFC系统下）
4 支持和反对连续统假设的辩论
5 广义连续统假设
6 参考条目
7 参考资料
8 外部链接
作为希尔伯特第一问题
主条目：希尔伯特的23个问题
1900年，大卫·希尔伯特以“连续统假设是否成立”作为“希尔伯特第一问题”。Kurt Godel和Paul Cohen确定了连续统假设在ZFC系统下，加上了选择公理，也不能证明或证否。 连续统假设简记CH。选择公理简记AC。
集合的大小
主条目：基数
要正式地列出这个猜想，我们需要一些定义：假如两个集合S与T之间存在着一个双射，我们会说这两个集合拥有相同的基数。直观的意思是在“T的每个元素只能配上仅仅一个S的元素，反之亦然”这个前提下，把S与T的元素拿出来配对是可能的。因此，集合{蕉，苹果，橙}与集合{黄，红，绿}拥有相同基数。
当情况去到如整数集或有理数集等无穷集的情况时，事件就变得复杂得多。当考虑所有有理数的集合时，有些初学者可能会直觉地认为有理数理所当然地多于整数，而有理数又显然少于实数，因此把连续统假设证否。但透过简单集合论的方法，我们能证明有理数集能与整数集形成一双射，因此有理集跟整数集有着一样的大小，而它们都被称为可列集。对角论证法则证明了整数集跟连续统（实数集）的基数并不一样。
连续统假设亦指出，实数集中每一个子集，要么和整数集有相同的基数，要么和实数集有相同的基数。
如果一一映射的两个集合的基数不一定相等，那么怎么办？ 这时，ZF需要增加FAC（AC的升级版本）。FAC主要用于解释AC。定义 若一一映射的若干集合的基数一定相等，则这些集合叫做标集；否则，这些集合叫做泛集。标集有基数，泛集无基数。定义 对于若干泛集，若强制按其中一个，来解释这些泛集的基数，则这些泛集叫做标泛集。标泛集有基数。定义 标集之间的一一映射叫做标射。泛集之间的一一映射叫做泛射。标泛集之间的一一映射叫做标泛射。性质 标射假设等价于有限元AC，标泛射假设等价于AC，泛射假设等价于FAC。[来源请求]
证明或证否的不可能性（在ZFC系统下）
康托尔相信连续统假设是对的，花了很多年尝试证明它，结果徒劳无功。它成为了希尔伯特那重要难题名单中的第一条，并在1900年巴黎的国际数学家大会上宣布此事。在那个时候，还没有公理化集合论的概念。
库尔特·哥德尔在1940年指出连续统假设不能在ZFC系统下证否，即使接受了选择公理为前提。保罗·寇恩在1963年证明了连续统假设同样不能在ZFC下被证明。因此，连续统假设“逻辑地独立于”ZFC。这些结果都是以ZFC的公设系统本身并不存在自相矛盾（相容性）为假设大前提，而这个大前提是被广泛接受为对的。
连续统假设并非被证明跟ZFC互相独立的第一个命题。哥德尔不完备定理一个立即的结论在1931年被发表，那是“‘存在着一个正式命题表达ZFC的相容性’乃独立于ZFC”。有别于纯粹数学的，这个一致的命题乃是有着在数学之上的特性。连续统假设和选择公理乃是最先被证明跟ZF集合论独立的命题。在Paul Cohen在1960年代发展出力迫法以前，这些独立性的证明并没有完成。
连续统假设与数学分析、点集拓扑学和测度论中很多的命题有紧密关系。由于其独立性，很多这些范畴中的猜想也就被证明了其独立性。
支持和反对连续统假设的辩论
哥德尔相信连续统假设是错的，而他对于连续统假设相容性的证明，只表示了ZF系统的公理有缺陷。哥德尔是一个柏拉图主义者，因此独立于一个命题的可证性而宣称其正确或错误，对他来说并无问题。寇恩也倾向于反对连续统假设。
历史上，喜欢一个“丰富”而且“大”的全集的数学家倾向反对连续统假设；而喜欢一个“整齐”而且“可控制”的全集的数学家则倾向支持连续统假设。对于能推导出连续统假设的可建造公理，一直以来也有一些支持与反对的争论。最近，Matthew Foreman更指出本体论的多元主义对支持连续统假设有利（Maddy 1988, p. 500）。这是因为在各种模型里面，支持连续统假设的模型往往会存在更多集合。
另一个观点是对于集合的幼稚概念并不足够明确地使我们能分辨究竟连续统假设是对是错。这个观点被“连续统假设对于ZFC系统的独立性”所支持，由于这些公理足够建立集合与基数的基本特性。要反对这一观点，要是能展示一条既能被直观所支持、又能从证明或证否面解决连续统假设的新公理，那就很足够了。尽管可建造公理能解决连续统假设，但它比较起连续统假设的反题并不显得更直观地正确。
至少有另外两个可推导出连续统假设的公理被提出，即使它们目前还没有被数学社群所广泛接受。在1986年，Chris Freiling展示了一个反连续统假设的论点，透过显示连续统的反题跟Freiling对称公理──一个跟概率有关的命题──等价。Freiling相信这条公理“直观正确”，但其它人反对。一个由W. Hugh Woodin发展的困难论点同样反连续统假设，并自2000年开始获得了值得考虑的注意。Foreman (2003)并没有完全反对Woodin的论点但敦促小心谨慎。[来源请求]
可以证明，直观正确的Freiling对称公理是个假命题。[来源请求]也可证明，貌似正确的AC也是一个假命题。[来源请求]AC的创立者策梅罗，用一双鞋与一双袜，比喻选择公理。然而，他凭什么让选择公理是一双鞋呢？只为确定与方便。[原创研究？]类似，康托尔他凭什么让“一一映射的两个集合的基数相等”？只为确定与方便。[原创研究？]确定性固不可少，方便性未必就好。[原创研究？]
广义连续统假设
GCH意味着这个严格的不等式对无限序数和有限序数都成立。
最新的FAC表明，GCH拥有多个实例。不妨GCH的两个实例是GCH1与GCH2。GCH1的第n个基数可不等于GCH2的第n个基数。GCH有一个特殊的实例，这个实例是唯一的，叫做终极连续统假设（Final continuum hypothesis，简记FCH）。
参考条目
阿列夫数
希尔伯特的23个问题
Beth数
序数
ZFC系统无法确定的命题列表
首个不可数序数
参考资料
Arens, Tilo; Frank Hettlich, Christian Karpfinger, Ulrich Kochelkorn, Klaus Lichtenegger, Hellmuth Stachel. Mathematik, Aufl. 3. Springer Spektrum. 2015. ISBN 978-3-6424-4918-5.
Cohen, P. J. Set Theory and the Continuum Hypothesis. W. A. Benjamin. 1966.
Cohen, Paul J. The Independence of the Continuum Hypothesis. Proceedings of the National Academy of Sciences of the United States of America. Dec 15, 1963, 50 (6): 1143–1148.
Cohen, Paul J. The Independence of the Continuum Hypothesis, II. Proceedings of the National Academy of Sciences of the United States of America. Jan 15, 1964, 51 (1): 105–110.
Dales, H. G.; W. H. Woodin. An Introduction to Independence for Analysts. Cambridge. 1987.
Foreman, Matt. Has the Continuum Hypothesis been Settled? (PDF). 2003 [February 25, 2006].
Freiling, Chris. Axioms of Symmetry: Throwing Darts at the Real Number Line. Journal of Symbolic Logic. 1986, 51 (1): 190–200.
Gödel, K. The Consistency of the Continuum-Hypothesis. Princeton University Press. 1940.
Gödel, K.: What is Cantor's Continuum Problem?, reprinted in Benacerraf and Putnam's collection Philosophy of Mathematics, 2nd ed., Cambridge University Press, 1983. An outline of Gödel's arguments against CH.
Kemmerling, Andreas. Informationsimmune Unbestimmtheit. Bemerkungen und Abschweifungen zu einer klaffenden Wunde der theoretischen Philosophie. Forum Marsilius Kolleg. 2012, 01: 1–43. doi:10.11588/fmk.2012.0.9407.
Maddy, Penelope. Believing the Axioms, I. Journal of Symbolic Logic. June 1988, 53 (2): 481–511.
Martin, D. (1976). "Hilbert's first problem: the continuum hypothesis," in Mathematical Developments Arising from Hilbert's Problems, Proceedings of Symposia in Pure Mathematics XXVIII, F. Browder, editor. American Mathematical Society, 1976, pp. 81–92. ISBN 978-0-8218-1428-4
McGough, Nancy. The Continuum Hypothesis.
Woodin, W. Hugh. The Continuum Hypothesis, Part I (PDF). Notices of the AMS. 2001a, 48 (6): 567–576.
Woodin, W. Hugh. The Continuum Hypothesis, Part II (PDF). Notices of the AMS. 2001b, 48 (7): 681–690.
左孝凌, 李为鉴, 刘永才. 离散数学. 上海科学技术文献出版社. 1982. ISBN 978-7-8051-3069-9.
