“反直觉”
让我们应接不暇,疲惫不堪
勇于抛弃既有观念,坦然面对一切
你就会发现
生活也并没有变的更好
恩,看视频吧
扩展猫粮
1. 这不是你的体重
我见过很多‘不笑的猫’,但我从来没见过‘不猫的笑’
本小节特别鸣谢:BBC NEWS
刘易斯·卡罗尔(Lewis Carroll)的代表作《爱丽丝漫游奇境》中有一幕经典场景:柴郡猫(Cheshire Cat)的身体逐渐消x容却奇迹般的保留了下来。见到此情此景,爱丽丝不禁惊呼:“我见过很多‘不笑的猫’,但我从来没见过‘不猫的笑’,这简直不可思议!”

这种
物体和属性分离
的现象完全脱离了我们的日常生活。这就好像在说,你在1号轨道扔了一个保龄球出去,它的旋转却出现在2号轨道。怎么可能呢?
根据量子力学,确实可能发生类似的事儿。比如说在某些特殊条件下,一个中子能和它的某个物理属性脱离开来,二者分别处于空间中两个不同的位置。
为了验证这一观点,科研人员在法国著名的
劳厄-朗之万研究所
(ILL)做了一个实验:他们利用硅晶体将中子束一分为二——就像在机场安检时,乘客和行李分开一样,然后通过专业设备检测中子的磁矩。
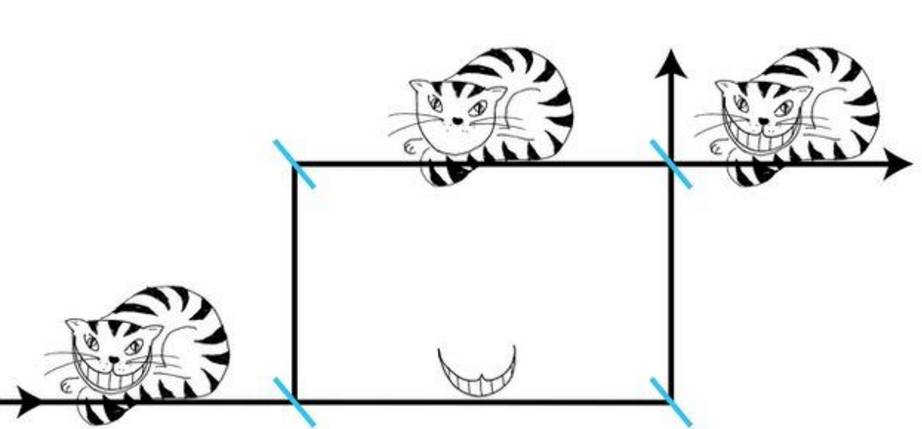
“看上去就好像中子走了一个通道,而中子的磁矩却走了另一个通道。”一位实验人员说道,“这种量子柴郡猫效应有很大应用价值。
有时粒子的磁矩会干扰某项重要的待测数据,现在我们或许能把磁矩甩到一旁了
。”
(原文地址 http://www.bbc.com/news/science-environment-28543990)
2. 靠谱的霍格沃兹特快列车
“这个章节看上去很复杂,可以直接跳到下个章节”
——鲁迅
本小节转载自 Matrix67 的 Blog
如果公交车发车的时间足够随机,概率均等地分布在时间轴上
(假设平均间隔仍是 10 分钟),那么当你来到车站时,平均需要多久才能等到公交车呢?答案或许很出人意料——
平均等待时间就是 10 分钟
。下面我们就来证明这一点。
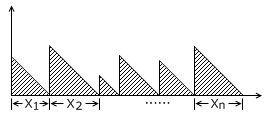
首先注意到,如果发车间隔依次为 X1, X2, …, Xn ,出现在车站的时刻不同,等候时间也会不同,其函数图象大致是锯齿形的。而平均等待时间,就是这个函数图象的平均高度,或者说所有阴影部分的面积和(也就是 X1, X2, …, Xn 的平方和的一半)除以这段时间总长(也就是 X1, X2, …, Xn 的和)。如果用 W 来表示平均等待时间的话,则
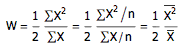
另外,由于公交车的发车时间是完全随机的,因而发车间隔长度服从
指数分布
λe^(
-λx
),它的平均值 μ = 1/λ ,方差 σ
^
2= 1/λ^2 ,后者正好是前者的平方。如果把上述所有 X 的方差记作 Var(X),那么
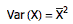
但是
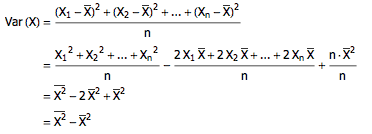
因此
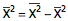
也就是
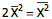
所以说
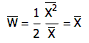
这就表明,
平均等待时间就是平均间隔时间
!
当然,转念一想,你会发现这其实并不难理解。由于发车时间是完全随机的,过去的都已经过去了,并不会对未来造成影响。也就是说,当你开始等车时,知道前面那趟车已经走了很久了,并不意味着下一班车就会更快到来。不管你出现在时间轴的什么位置,等到下一班车的期望时间都是一样的——平均的间隔时间。
(原文地址 http://www.matrix67.com/blog/archives/4349)
3. 虽然长度短,但不一定快呀
这个问题在17世纪欧洲数学圈激起了轩然大波儿
本小节特别鸣谢:果壳用户 @aifreedom
在忽略摩擦力、只考虑重力的情况下,
一个速度为零的质点站在高处的A点,只有沿着摆线下滑,才能用最短的时间到达低处的B点
。这就是
最速降线问题




