比方说，神经网络不见得比决策树好，同样反过来也不成立。

最后的结果是有很多因素在起作用的，比方说数据集的大小以及组成。

当然，你要选适合解决你问题的算法来尝试。

比方说，要打扫房子，你会用真空吸尘器，扫把，拖把；你绝对不会翻出一把铲子来开始挖坑，对吧。

00 大的原则

不过呢，对于所有预测建模的监督学习算法来说，还是有一些通用的底层原则的。

机器学习算法，指的是要学习一个目标函数，能够尽可能地还原输入和输出之间的关系。

然后根据新的输入值X，来预测出输出值Y。精准地预测结果是机器学习建模的任务。

So，Top10机器学习算法，了解一下。

01 线性回归

统计学与机器学习领域里研究最多的算法。

做预测建模，最重要的是准确性（尽可能减小预测值和实际值的误差）。哪怕牺牲可解释性，也要尽可能提高准确性。

为了达到这个目的，我们会从不同领域（包括统计学）参考或照搬算法。

线性回归可用一条线表示输入值X和输出值Y之间的关系，这条线的斜率的值，也叫系数。

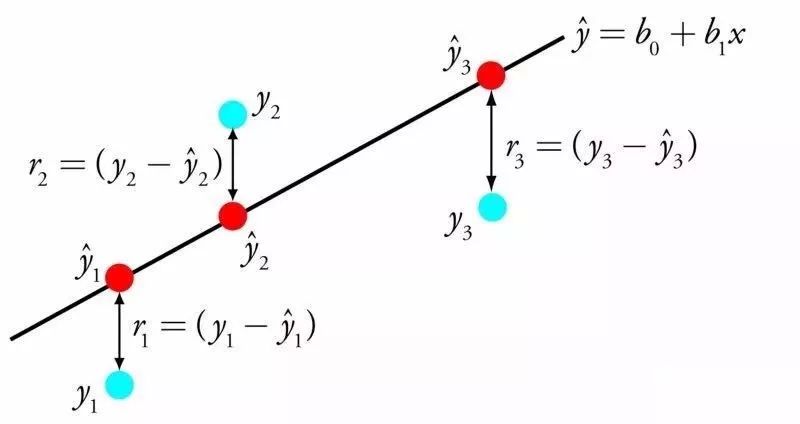
比方说，y = B0 + B1*x

我们就可以根据X值来预测Y值。机器学习的任务就是找出系数B0和B1。

从数据中建立线性回归的模型有不同的方法，比方说线性代数的最小二乘法、梯度下降优化。

线性回归已经存在了200多年，相关研究已经很多了。用这个算法关键在于要尽可能地移除相似的变量以及清洗数据。

对算法萌新来说，是最简单的算法了。

02 逻辑回归

这方法来自统计学领域，是一种可以用在二元分类问题上的方法。

逻辑回归，和线性回归相似，都是要找出输入值的系数权重。不同的地方在于，对输出值的预测改成了逻辑函数。

逻辑函数看起来像字母S，输出值的范围是0到1。

把逻辑函数的输出值加一个处理规则，就能得到分类结果，非0即1。

比方说，可以规定输入值小于0.5，那么输出值就是1。

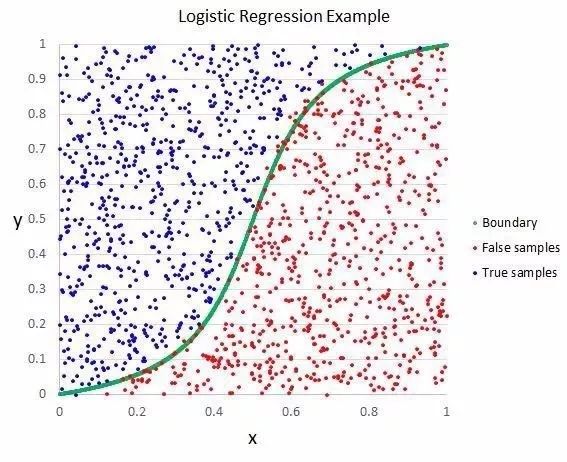
▲逻辑回归

这个算法还可以用来预测数据分布的概率，适用于需要更多数据论证支撑的预测。

和线性回归相似，如果把和输出不相干的因子或者相近的因子剔除掉的话，逻辑回归算法的表现会更好。

对于二元分类问题，逻辑回归是个可快速上手又有效的算法。

03 线性判别分析

逻辑回归算法，只能用于二分问题。

当输出的结果类别超过两类的时候，就要用线性判别分析算法了。

这种算法的可视化结果还比较一目了然，能看出数据在统计学上的特征。这上面的结果都是分别计算得到的，单一的输入值可以是每一类的中位数，也可以是每一类值的跨度。

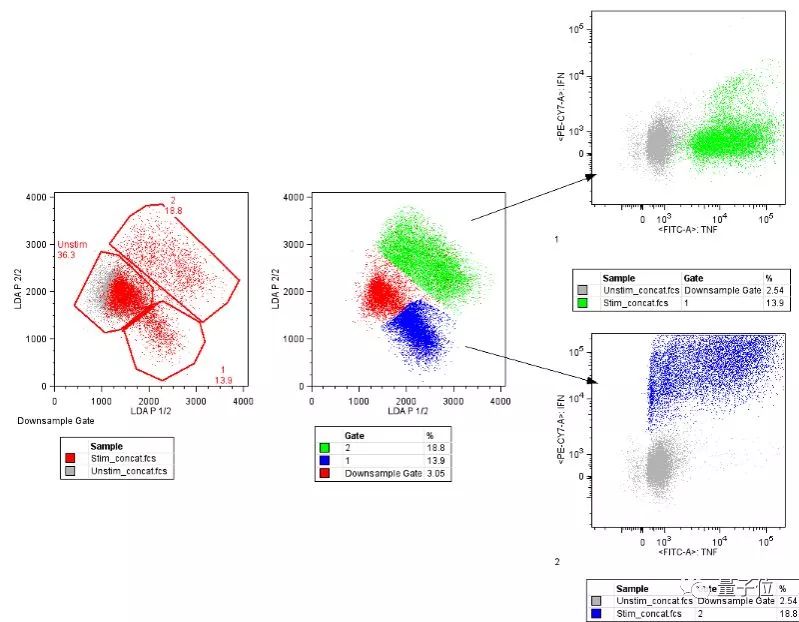
▲线性判别分析

基于对每种类别计算之后所得到的判别值，取最大值做出预测。

这种方法是假定数据符合高斯分布。所以，最好在预测之前把异常值先踢掉。

对于分类预测问题来说，这种算法既简单又给力。

04 分类与回归树

预测模型里，决策树也是非常重要的一种算法。

可以用分两叉的树来表示决策树的模型。每一个节点代表一个输入，每个分支代表一个变量（默认变量是数字类型）

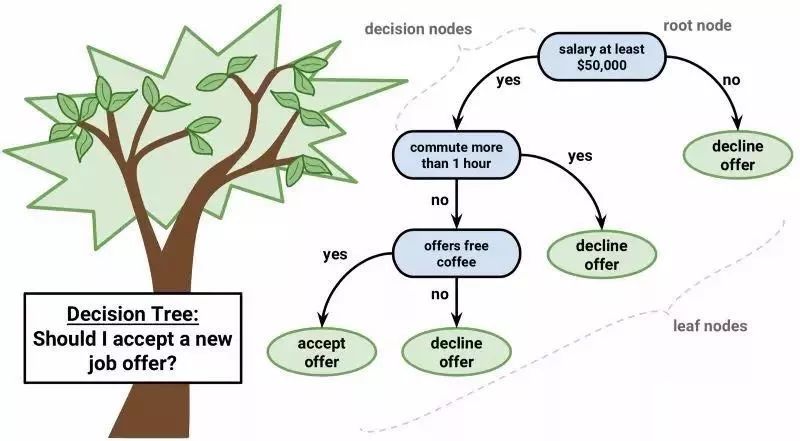
▲决策树

决策树的叶节点指的是输出变量。预测的过程会经过决策树的分岔口，直到最后停在了一个叶节点上，对应的就是输出值的分类结果。

决策树很好学，也能很快地得到预测结果。对于大部分问题来说，得到的结果还挺准确，也不要求对数据进行预处理。

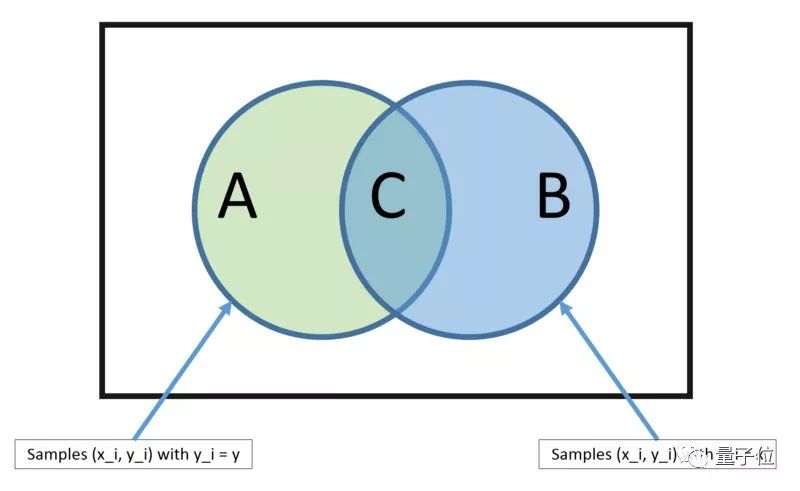
05 朴素贝叶斯分类器

这种预测建模的算法强大到超乎想象。

这种模型，可以直接从你的训练集中计算出来两种输出类别的概率。

一个是每种输出种类的概率；另外一个，是根据给定的x值，得到的是有条件的种类概率。

一旦计算之后，概率的模型可以用贝叶斯定理预测新的数据。

当你的数据是实数值，那么按理说应该是符合高斯分布的，也就很容易估算出这个概率。

▲贝叶斯定理

朴素贝叶斯定理之所以名字里有个“朴素”，是因为这种算法假定每个输入的变量都是独立的。

不过，真实的数据不可能满足这个隐藏前提。尽管如此，这个方法对很多复杂的问题还是很管用的。

06 K近邻算法

最近K近邻的模型表示，就是整个训练集。很直截了当，对吧？

对新数据的预测，是搜索整个训练集的值，找到K个最近的例子（literally的邻居）。然后总结K个输出的变量。