
欢迎投稿计量经济圈邮箱:
[email protected]
上一篇文章 第二篇因果推断经典,工作中断对工人随后生产效率的影响?
由于小编的失误,在文章末尾处写着“获得PDF版本,给推文作者打赏1元”。推文作者本意是公开这个推文PDF的,以方便大家的查阅和交流,而且附在了文章评论区。给推文作者带去的烦扰和读者带来的不便,咱们所有小编都感到很抱歉。
通告:请圈友 闫文收 和 王阳,联系计量经济圈公邮,你们可以进入Ca文献交流小组。
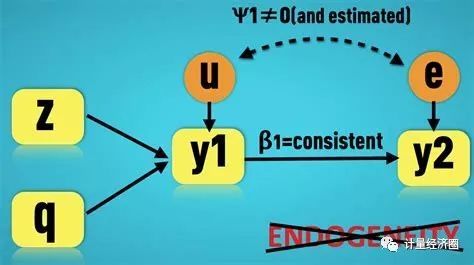
内生性(endogeneity)的概念跟内生变量(endogenous variable)的概念息息相关。而内生变量这一概念的兴起又跟社会科学的模型化和系统化密不可分。比如曼昆在他的经济学原理(或者是宏观经济学?)一开头就举了一个汉堡包的例子:在汉堡包的生产中,有投入(原料、劳动、工厂),有产出(汉堡包),我们感兴趣的是中间的制作流程。那么研究者应该做的,是通过一个模型来刻画上述制作流程(比如一个生产函数),从而给定模型的输入(各类投入品的消耗),就能计算出对应的输出(汉堡包产量)。在得到了准确的模型之后,我们就可以进一步对汉堡包的生产进行预测和改进,达到理解世界和改造世界的目的。在这个例子中,投入就是汉堡包制造模型中的外生变量,而产出则是内生变量。换言之,外生变量是模型中的 “原因”,而内生变量是模型中的 “结果”。
很明显,这种思考问题的方法带有浓重的控制论色彩,将任何社会现象都看作一个包含了输入、输出和模型三部分的系统(或许是二战期间大批巨型工程,比如曼哈顿工程的遗产?)。在政治学里,这种视角导致了大卫·伊斯顿(David Easton)的系统主义尝试(今天的影响力已然不大)。而在经济学中,其结果是学者们开始将宏观经济的运行作为一个包含了数十乃至数百种输入和输出的巨大系统加以处理,以至于联立方程模型在五六十年代变得非常流行。学者们认为,可以用一大堆线性方程来表示各个宏观指标(比如物价、失业率、利率等等)之间的关系,从而为政府的经济政策指定提供参考(当然凯恩斯主义的发展在其中也扮演了重要角色)。
我们都知道,在一个回归方程里,等号左边是因变量,右边是自变量。在联立方程模型里,我们有几十乃至几百个方程,所以每个变量都可能同时出现在方程 A 的左手边和方程 B 的右手边。也就是说,这些变量的值既被其他变量决定,又能够影响另外一些变量。它们在整个模型中起了中间环节的作用,因此被称为 “内生变量”(只出现在左手边的变量显然也是内生的)。如果我们假设每个变量都是内生的,那模型中的参数就会太多,以至于根本无法估计(不可识别)。所以,研究者必须根据理论或者现实观察,对模型加以简化,假设某些变量只出现在各个方程的右手边,这些纯粹的 “输入” 就被称为 “外生变量”。正是外生变量的存在,使得我们可以 “识别(identify)” 模型中的参数。
举个最简单的例子,经济学里基本的供求模型告诉我们,供给曲线(p = a + bq)和需求曲线(p = c - dq)共同决定了价格(p)和交易量(q)。然而现实中我们能够观察到的,只是一组均衡时的 p 和 q,基于这个数据,我们用回归只能得到斜率和截距两个参数的估计值。但供给曲线和需求曲线里一共有四个参数(a b c d)。此时,通过回归这种 “简约式(reduced form)” 估计得到的参数,无助于我们得知 “结构式(structural form)” 模型中的 “深层参数(deep parameter)”。我们的系统里的p和q都是内生变量,所以才会出现无法识别的情况。怎么解决这个问题呢?经典的办法是,假定存在着某个不影响需求,只影响供给(或者反过来)的外生变量。比如在渔业中,海上的坏天气很可能阻碍渔船出海,形成一个供给侧的冲击,但应该不会改变人们对海产品的需求。根据天气的变化,我们就有可能估计出全部的四个参数。事实上,这也是 “工具变量(instrumental variable)” 这一估计方法的起源。
从今天的角度来看,联立方程模型当然充满了各种问题:为什么方程都是线性的?这么多关系式是从何推导而来?因此在经济学和政治学中,这套方法已经不再时兴。但是,这整个体系时至今日,还在很大程度上左右着社会科学家们对实证研究的评判。当我们写下一个回归方程的时候,其实已经假定了:1. X 是 “外生变量”,而 Y 是“内生变量”,2. 整个系统中或者不存在其他方程,或者其他方程的存在不影响当前方程的估计结果。因此,当人们说你的模型有内生性问题的时候,他们的意思其实是:有没有可能真实的系统中实际上有另外一个方程,在其中当前的 X 位于等号左边?在这个方程中,如果右端是 Y,我们就说 X 和 Y 互为因果;如果右端是另一个变量 Z,我们就说存在遗漏变量。这也就是导致内生性的两个基本原因。假如真实系统里有两条方程,你只用 OLS 估计了一条,那么因果链条的一部分就被忽视了,得到的估计也就无法反映系统中的实际情况。
那么,怎么避免出现内生性问题呢?基本的思路有两种。一是用 “简约式(Reduced Form)” 估计,亦即做实验或者找一个自然实验。这种情况下,X 完全由实验者或者 “自然” 决定,从而在系统中不会出现在任何方程的左手端。工具变量从本质上来说,就是一个自然实验。二是用 “结构式(Structural Form)” 估计,也就是写一个模型,从 “深层参数”,比如偏好、技术条件、资源禀赋等要素出发,推导出整个体系中各个 agent 之间的相互关系。这时候,我们可以 argue 说,我们的模型准确地反映了现实情况,也就是穷尽了变量之间可能存在的各种关系(或者从联立方程的视角出发,找到了系统中全部的方程)。接下来,我们可以用最大似然或者广义矩估计这样的方法,同时估计从模型中推导出的全部关系式,得到相应的参数。
两种思路各有优劣。简约式依赖于实验或者自然实验的有效性,而在社会科学中这很多时候都无法保证。另外,即使估计出了准确的参数,我们得到的也只是整个系统之中一条逻辑链条(一个方程)所包含的信息。对于系统中可能存在的其他关系,我们还是一无所知。而且在自然实验中得到的结论,能在多大程度上代表一般性的情况,也是个很大的问题。相比之下,结构式估计可以告诉我们整个系统的普遍性规律。利用估计出的深层参数,我们可以很方便地得到各种假想情况下会出现的结果(反事实推断)。但怎么保证我们的模型确实是现实世界的近似呢?其实还是要依赖于(甚至比自然实验更强的)假设。经济学目前的潮流,是把两种思路结合起来:写出模型之后,用自然实验来推断参数。这种方法更加可信,但对于研究者的要求也更高。
上面讲了半天好像都是在讲经济学。从我个人的观点来看,“内生性” 确实是一个经济学家喜欢用的名词。对社会规律的模型化和系统化在经济学中进行得格外彻底,而只有从模型和系统的角度出发,内生性这个词才显得比较有意义。相比之下,政治学和社会学中的理论更像是散落各处的命题,而非完整体系中的一个部分。所以,这两个学科中 formal model 比较少,用 model 来做结构化估计的尝试就更加罕见。政治学和社会学中的实证研究,其实更加贴近统计学的路数,不愿意仰仗模型(回归方程),而更偏好 agnostic 的估计方法(匹配,机器学习等等)。只是因为 “经济学帝国主义” 的渗透,内生性的概念才进入到了其他社会科学之中,并在很多时候被当作了 “unconfoundedness”(即给定协变量之后 treatment 和 potential outcome 相互独立)的同义词。不过,如果我们不从 Rubin Model 出发,而是把 Pearl 的因果图作为实证研究的参照系,那么内生性在因果推断中还是有其位置的。
内生性问题是计量经济学中必须重视无法回避的问题,内生性一般就是认为扰动项中存在和解释变量相关的可能,这会导致参数估计的有偏甚至不一致,所以一般都要检验模型的内生性问题,可以找本书学下Hausman检验判断内生性的方法和IV估计的使用。
注:上文来自王也/ 纽约大学政治学博士生。
从最根本的定义来说,内生外生首先是取决于系统的,在一个系统内部决定的变量,自然就是内生变量,在系统决定的变量,就是外生变量。比如,给一个系统,比如地球,那么当前情况下地球上一切可以统计的变量都是内生变量,但是阳光就是外生变量。那么如果以太阳系为研究的系统,那么自然,阳光此时也是内生变量了。
这样说内生性外生性似乎很容易理解,但是涉及到经济问题似乎不是那么好办了,因为经济系统中,所有的变量很难说是完全独立的,比如货币发行量,似乎是央行决定,按理说是外生的吧,但是慢着,央行的货币不是随便发的,也是因为有经济体有需求才会向社会发行货币,这个就是货币外生和货币内生的讨论,研究的文章有很多。
还是先说外生性吧,Leamer定义,如果y对x的条件分布(这个就是给出x值,对应随机变量y)不随x的生成过程的修正而发生变化,那么x就是外生变量。外生性似乎还是可以分为两类,前定性(前定变量是指独立于方程中同期和未来误差项的变量),严格外生(严格外生变量是指独立于方程中所有同期、未来,和过去误差项的变量)。
依照这个定义,我什么也看不出来,倒是可以从CLRM假定cov(Ut,Xt)≠0情况考虑。既然cov(Ut,Xt)≠0可以叫成内生性,那么cov(Ut,Xt)=0大概可以叫外生变量了吧。chris的书前面把这个假定强化为X是非随机变量,当显然这一假定是靠不住的,X更多情况下是随机变量。这里涉及到前面曾经困惑的一个概率,随机解释变量,随机解释变量就是说解释变量是随机的,原因根据我的思考总结,大概是这两类,1.观测值存在误差2.根据Y=α+θX+μ,如果Y能影响X,由于Y是随机的,自然X也就带有随机性了。
随机解释变量容易带来内生性的问题,但却也不是必然,比如X是随机解释变量,但是X和u是独立的,也就是说cov(Ut,Xt)=0的时候,是不违背CLRM假设的。其实到这里,我们讨论的一切,什么内生性,自相关,异方差,这些为什么要讨论呢,就是因为我们经常用OLS模型进行估计,而CLRM的五个假定就是为了使得OLS的估计具有一致性,无偏性,有效性。这时候,你看,即使X是随机变量,如果cov(Ut,Xt)=0,那么是用OLS模型估计的值仍然是具有上面三条性质的,也就是说回归没有问题。什么时候会出问题,cov(Ut,Xt)≠0,这个时候的回归就不是一致的了,这个可以从无偏定义推出来通过估计式,然后将cov(Ut,Xt)≠0代入入就可以发现E(β)≠β等等类似,这个不是今天论述的重点。
顺带第一下CLRM第五条假设,残差u服从正太分布,这个和估计值的一致无偏有效性没有关系,但是在进行有效性检测是,就要用到这个假设了,如果残差不符合正太分布,根本就没办法进行任何检测了。不过好在根据中心极限定理,样本够多的时候,可以渐进趋向正太分布,拿来做有效性检测也不会有太大问题。
回到内生性的话题,解释变量的内生性指的是模型中的解释变量与扰动项相关,这个问题可以的原因大体有以下几条:
1 模型设定偏差,遗漏了变量,这样,被遗漏的变量就被放进了残差项了,如果对被解释的变量和其他解释变量相关,自然,就会出现cov(Ut,Xt)≠0也就是内生性问题了。
2测量误差,测量误差也有两种,一种是对被解释变量Y的测量误差,这个其实不会引起内生性,另一种是对解释变量X的测量误差。说明一下,被解释变量Y的测量误差,设y的真实值y*,测量值y,测量误差e0=y-y*,假设理论的回归方程为y*=β0+β1x1+….将测量误差带入方程得y*=β0+β1x1+….ε+e0=y*=β0+β1x1+….ν其中ν=ε+e0表示实际回归方程的残差,显然由于y的测量误差和xi是相互独立的,那么实际回归方程的残差v也与各解释变量相互独立(无关),所以还是满足外生性的。至于解释变量x的测量误差,回归式y=β0+β1x1+….ε中,测量误差产生于xk, ek=xk-xk*,将测量误差带入回归式y=β0+β1x1+….ε+βke那么如果cov(x*k,ek)=0,那么cov(xk,ek)=cov(x*k+ek,ek)=σ^2,此时的测量误差便会引起内生性的问题了。
3双向交互影响(或者同时受其他变量的影响)这种情况引起的内生性问题在现实中最为常见。其基本的原理可以阐述为,被解释变量y和解释变量x之间存在一个交互影响的过程。x的数值大小会引起y取值的变换,但同时y的变换又会反过来对x构成影响。这样,在如下的回归方程中:y=β0+β1x1+….ε如果残差项ε的冲击影响了y的取值,而这样的影响会通过y传导到x上,从而造成了x和残差项ε的相关。也就是引起了内生性问题。这里举几个简单、但经常遇到的例子说明。
例1:金融发展与经济增长 例2:外商直接投资FDI与经济增长 例3:犯罪率与警备投入。而我们通常最难以确定的内生性问题就是这个问题,因为经济学领域,变量大多都是相互影响的,毕竟都是在这样一个社会系统里面。而我们之前那些讨论的内容,通常都不是我们遇到的主要问题,因为测量误差是既成事实,改进很困难,而遗漏变量,这个是模型设定的时候,如果你遗漏了,别人挑刺也很难找出你遗漏了什么。倒是最后的交互影响,因为几个解释变量放在那里,他想挑刺就说内生性,因为经济系统内部内生性很多,如果你不能很好的解释,检验,这一道关就不能让别人信服。
网上有人说,内生变量和外生变量很好区别:外生变量就像函数中的参量一样,不受模型内部变量的影响。而内生变量受模型中的变量影响,比如X+Y=a (1)X-Y=1 (2)将上面两个方程联立,可以得到一个模型,其中变量X 和Y是可以通过解方程从“模型中”解出的,故是内生变量。但是变量a无法通过解方程来决定,只能由外在因素决定,所以是外生的,相当于一个参数。这种说法倒是简单明了,很容易理解,也符合我们的直觉,但是在简历模型的时候,很多时候没有办法就是说a他就是外生的,他不是另外一个变量Z。
计量经济圈内生性交流小组
写在后面:各位圈友,咱们的计量经济圈社群里面资料和计量咨询都很多,希望大家能够积极加入咱们这个大家庭(戳这里)。之后我们会逐步邀请社群里的圈友再直接建立微信群与圈圈对话,进去之后一定要看“群公告”,不然接收不了群信息。
提议
欢迎各位投稿给计量经济圈,各种文献笔记、计量技巧和最新发现都可以实名在这里发出来,让你在这个圈子积累声誉和将来的合作文章合作机会。


















