五、曲线运动
1
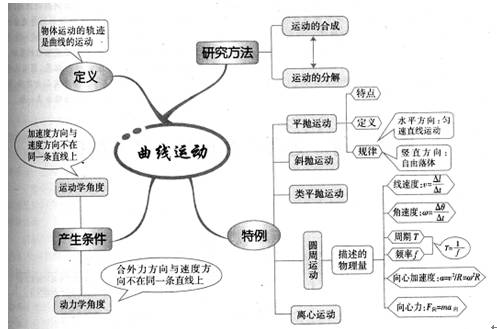
.曲线运动
⑴物体作曲线运动的条件:
①初速度和
合外力不为零
。②两者
不在一直线上
。
⑵速度:
①合外力的作用是改变速度(大小、方向)。
②任一点的速度方向在该点曲线的切线方向上。
③
运动中速度不断改变,是一种变速运动,如果合外力是恒定的,属匀变速运动。
2
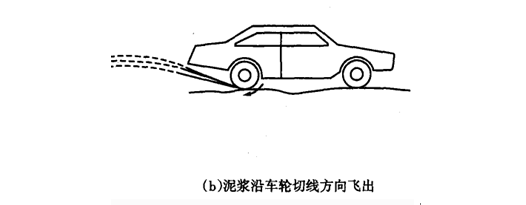
.运动的合成和分解
1
、从已知的分运动来求合运动叫运动的合成,包括位移、速度和加速度的合成,由于它们都是矢量,所以
遵循平行四边形定则
。
2
、求一个已知运动的分运动,叫运动的分解,
解题时应按实际“效果”分解,或正交分解
。
3
、合运动与分运动的特征:
①等时性:合运动所需时间和对应的每个分运动时间相等。
②独立性:一个物体可以同时参与几个不同的分运动,各个分运动独立进行,互不影响。
速度的合成和分解一定要依据其实际效果进行,合运动一定是物体的实际运动。(换句话说,物体实际运动方向是合速度的方向,即物体实际运动方向是平行四边形对角线的方向。)
4
、运动的性质和轨迹:
(1)物体运动的性质由加速度决定(加速度得零时物体静止或做匀速运动;加速度恒定时物体做匀变速运动;加速度变化时物体做变加速运动)。
(2)物体运动的轨迹(直线还是曲线)则由物体的速度和加速度的方向关系决定(速度与加速度方向在同一条直线上时物体做直线运动;速度和加速度方向成角度时物体做曲线运动)。
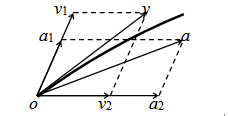
(3)两个互成角度的直线运动的合运动是直线运动还是曲线运动?
决定于它们的合速度和合加速度方向是否共线(如图所示)。
(4)常见的类型有:
①
a
=0:匀速直线运动或静止。
②
a
恒定:性质为匀变速运动,分为:
A.
v
、a
同向,匀加速直线运动;
B.
v
、a
反向,匀减速直线运动;
C.
v
、a
成角度,匀变速曲线运动(轨迹在v、a之间,和速度v的方向相切,方向逐渐向a的方向接近,但不可能达到。)
③
a
变化:性质为变加速运动。如简谐运动,加速度大小、方向都随时间变化。
5
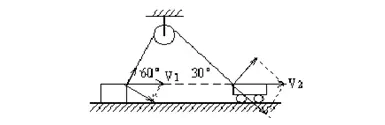
、渡河问题:渡河问题所涉及的就是渡河的最短时间问题和渡河的最短位移问题。
①
船渡河
:它是船在静水中的运动和水的运动的合运动,它是两种匀速直线运动的合成,合运动也是匀速直线运动。
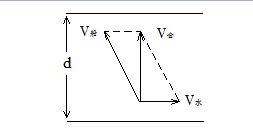
船渡河的时间由河宽和船垂直河岸的分速度决定,与水的流速度无关,船渡河沿河岸的位移与渡河时间和水的流速有关。
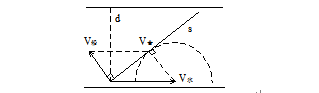
当船的静水速度大于水的流速时,可以使它们的合速度方向垂直河岸,此时渡河最小位移等于河宽,当船的静水速度小于水的流速时,无法使它们的合速度方向垂直河岸,
此时要通过画圆弧方法求解。
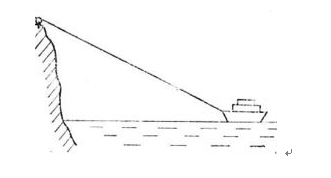
②
岸上拖船
:包括汽车通过滑轮提升重物问题,存在两个不同的运动,一般岸上的运动是匀速直线运动,而比岸低的水中船的运动是一种变速运动,船在水中的速度是合速度(实际效果),连接绳的速度是船的分速度(它的大小等于岸上拉绳力的速度大小),船的移动距离要通过绳被拖过的长度计算。如果是河中的船(匀速)拖动岸上物体,则船速也是合速度。对于汽车通过滑轮提升重物,汽车速度也是合速度。
3.
平抛运动
⑴性质
:
初速度与重力垂直
,是
匀变速运动
,加速度
=g
。
⑵分运动
:①水平方向
X=V0t
;竖直方向
Y=gt2/2
。②平抛运动的空中运动时间由h决定,水平位移由
h
和
V0
联合决定。③运动过程各点的水平分速度都等于
V0
,竖直分速度
Vt=gt
,速度改变量
gt
。④各点机械能相等。

4.
匀速圆周运动
1
、定义
:做圆周运动的物体,若在相等的时间里通过的圆弧长度相等,就是匀速圆周运动。
2
、运动学特征
:线速度大小、向心加速度大小不变,但方向时刻改变,故匀速圆周运动是变速运动。
⑴意义:
①速度
大小
不变,
方向不断改变
。②加速度
大小不变
,方向时刻改变,是变加速运动。
⑵物理量:
①线速度:V=S/t=2πR/T=Rω,其中S是通过的
弧长
,方向沿该点圆周的切线方向。
②角速度:ω=θ/t=2π/T,单位为rad/s。
③周期T和频率f:T=1/f,在匀速圆周运动中,转速n=f。
④向心加速度:a=V2/R=Rω2,方向始终指向圆心(不断变化)。
⑤向心力:大小F=ma=mV2/r=mrω
3
、向心力
:①作用效果:产生向心加速度,以不断改变物体的速度方向,维持物体做圆周运动。
②大小:
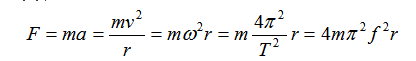
③ 产生:向心力是按效果命名的力,不是某种性质的力。
4
、向心加速度的分析
:向心加速度是向心力的效果,其方向与向心力相同,总是指向圆心。
从运动的角度看,向心加速度是描述做匀速圆周运动的物体的速度方向变化情况的物理量,其计算公式:
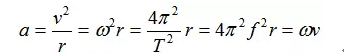
5
、圆周运动中向心力的特点:
(1)匀速圆周运动:由于匀速圆周运动仅是速度方向变化而速度大小不变,故只存在向心加速度,物体受到外力的合力就是向心力。可见,合外力大小不变,方向始终与速度方向垂直且指向圆心,是物体做匀速圆周运动的条件
(2)变速圆周运动:速度大小发生变化,向心加速度和向心力都会相应变化,求物体在某一点受到的向心力时,应使用该点的瞬时速度,在变速圆周运动中,合外力不仅大小随时间改变,其方向也不沿半径指向圆心,合外力沿半径方向的分力提供向心力,使物体产生向心加速度,改变速度的方向,合外力沿轨道切线方向的分力,使物体产生切向加速度,改变速度的大小。
6
、圆周运动中的临界问题:
竖直平面内的圆周运动是典型的变速圆周运动。一般情况下,只讨论最高点和最低点的情况,常涉及过最高点时的临界问题。
临界问题的分析方法
:首先明确物理过程,正确对研究对象进行受力分析,然后确定向心力,根据向心力公式列出方程,由方程中的某个力的变化与速度变化的对应关系,从而分析找出临界值。
(1)
“绳模型”
如图所示,小球在竖直平面内做圆周运动过最高点情况。(注意:绳对小球只能产生拉力)
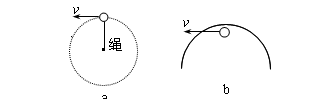
①小球能过最高点的临界条件:绳子和轨道对小球刚好没有力的作用
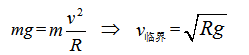
②小球能过最高点条件:
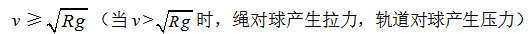
③不能过最高点条件:

(2)
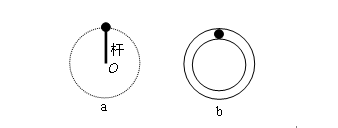
“杆模型”
如图所示,小球在竖直平面内做圆周运动过最高点情况(注意:轻杆和细线不同,轻杆对小球既能产生拉力,又能产生推力。)

(3)
圆锥摆
的情况:
如图所示,圆锥摆的情况是水平面内的圆周运动情况,将绳的拉力竖直分解与重力平衡,水平分解提供向心力,即:
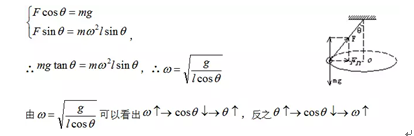
往期精彩回顾
高中知识点:
运动的描述|
匀
变速直线运动规律
|
相互作用考点及知识点
|
牛顿运动定律
初中知识点
质量与密度
|
常见的力
|
运动和力
|
压力压强
|
浮力|
简单机械
|
功与机械能
|声现象
|
光现象
物态变化
|
热与能
|
电流与电路
|
电压和电阻
|
欧姆定律
|
电能与电功率
|
电热与安全用电
|
电与磁
|
信息的传递|
能源与可持续发展





