

20世纪70年代,美国气象学家洛伦兹提出,亚马逊雨林一只蝴蝶偶尔振动翅膀,也许两周后就会引起美国得克萨斯州的一场龙卷风。尽管这个比喻有些哗众取宠,言过其实,但是它隐喻着我们生活中的种种现象:
初始条件十分微小的变化经过不断放大,将导致未来前景的巨大差异。
一位气象学家怎么会“杜撰”这么一个“蝴蝶”的寓言呢?这得从他的科学发现讲起:
为了预报天气,洛伦兹用计算机求解仿真地球大气的13个方程式,主要研究了三个非线性气象因素——温度、气压、风速——之间的关系,意图是利用计算机的高速运算来提高长期天气预报的准确性。完成冗长的计算之后,洛伦兹决定对结果进行复核,只保留小数点后3位,而不是原先的后6位。前后结果比较发现,两条曲线完全不一样。(这简直是不可思议的事啊!)
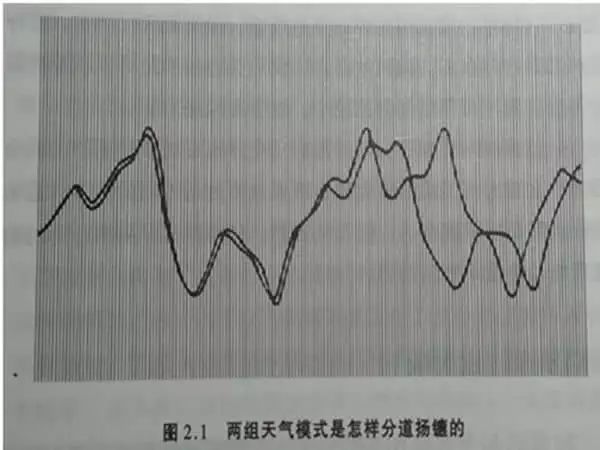
随后,洛伦兹完成了仿真地球大气的13个方程式的求解,并模拟出了不同条件下的图解,如图所示:
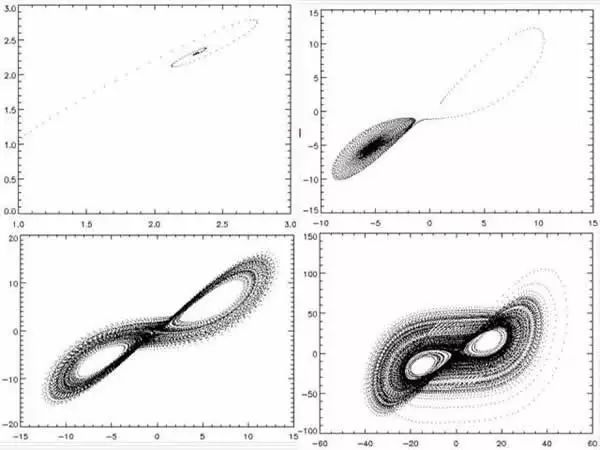
因为方程式的图解非常像一只张开翅膀的蝴蝶,结合之前发现的结论(一个微小的误差随着不断推移将造成巨大的后果),
洛伦兹创造了一个新的寓言故事——蝴蝶效应。
寓言终归是寓言,洛伦兹通过 “蝴蝶效应”的发现历程,发表了著名的论文《决定性非周期流》,首次从数值计算中发现非线性的初值敏感性和最重要的洛伦兹奇异子,第一次系统地揭示了发生在确定性系统中(方程式组成的确定性系统)的貌似随机的不规则运动(蝴蝶形状的运动轨迹),并将其命名为混沌运动。
因首次发现混沌现象,洛伦兹被称为混沌理论之父。
蝴蝶效应也成为了混沌理论的代名词。
古语有云:失之毫厘,谬以千里。千里之堤,以蝼蚁之穴溃;百尺之室,以突隙之烟焚。有一首翻译的英文诗写道:钉子缺,蹄铁卸;蹄铁卸,战马蹶;战马蹶,骑士绝;骑士绝,战事折;战事折,国家灭。
蝴蝶效应与混沌无所不在。上升的香烟柱破碎成缭乱的旋涡,旗帜在风中前后飘拂,龙头滴水从稳定样式变成随机样式。混沌出现在大气和海洋的湍流中,出现在飞机的飞翔中,出现在高速公路上阻塞的汽车群体中,出现在野生动物种群数的涨落、心脏和大脑的振动以及地下管道的油流中。
经济学家发掘出阵旧的股票价格数据,用混沌的方式加以分析。混沌直接介入了对诸如云彩的形状、闪电的踪迹、微血管的缠结、星体形成银河星团的过程等等的再认识。混沌不仅改变了天文学家看待太阳系的方式,而且开始改变企业家作出保险决策的方式,改变政治家谈论紧张局势导致武装冲突的方式,等等。
但是应该看到,与各种混沌理论研究的百花齐放的场面不大协调的是,混沌理论应用于解决当今系统中出现的各种现实问题的成果并没有那么璀璨。混沌理论的应用还存在许多争议。可以预见,混沌学今后最具价值的研究方向应该在其应用领域。
有的科学家对混沌理论评价很高,认为“混沌学是物理学发生的第二次革命”。但有的人认为这似乎有些夸张,认为它的应用前景有待进一步揭示。但混沌理论研究同协同学、耗散结构理论紧密相关。它们在从无序向有序和由有序向无序转化这一研究主题中有共同任务。在今后很长一段时间内,混沌动力学仍会是一门极具活力的学科。
本文综合自:非线性科学与医学沙龙、中华读书报、百度百科。
来源: 声振之家 2016-12-07
参考文献:
[1] EN. Lorenz,
Deterministic nonperiodic flow
, Journal of the atmospheric sciences, 1963.
[2] http://www.nytimes.com/2008/04/17/us/17lorenz.html.
[3] 马天,偏微分方程理论与方法,科学出版社,2011。
[4] Tian Ma and Shouhong Wang,
Phase Transition Dynamics
, Springer, 2014.
[5] V.I. Arnold,
Mathematical Methods of Classical Mechanics
, Springer GTM.
[6] Martin Golubitsky et. al,
Singularities and Groups in Bifurcation Theory
, Springer, 2000.
[7] Hansjörg Kielhöfer,
Bifurcation Theory: An Introduction with Applications to Partial Differential Equations
, Springer, 2012.
[8] https://en.wikipedia.org/wiki/Hopf_bifurcation.
[9] John Guckenheimer,
A Strange, Strange Attractor
, 1972.
[10] https://people.math.osu.edu/yang.2677/Lorenz.java.
[11] Takashi Matsumoto,
A Chaotic Attractor from Chua's Circuit
, 1984.
[12] B. M. Bolker and B. T. Grenfell,
Chaos and Biological Complexity in Measles Dynamics
, JSTOR, 1992.
[13] A. Wolf et. al,
Determining Lyapunov exponents from a time series
, 1981.





