作者:徐传胜
来源:http://blog.sciencenet.cn/blog-542302-938966.html
数学历史文化的沉淀,铸就了一个个美丽数学符号,其像颗颗璀璨明珠闪耀在数学时空。分式是分数的拓展,分数是分式的特例。无论是分式还是分数,自然都离不开分数线。我们现今应用分数线应是娴熟自然,其上方为分子,下方为分母。正是分数线这条美丽彩带连接起分子和分母。然而这条看似简单的横线却凝结着人类上千年的的智慧,蕴含着数学家对分数、分式的科学审视,其演进过程彰显着数学发展的内在动力。
1.古埃及的分数表示
史料表明:石器时代的古人尚未发现分数,而随着先进青铜文化的崛起,分数概念和分数记号应运而生了。古埃及象形文字创造了一种符号表示单位分数(分子为1的分数),即在整数上方画一个长椭圆,就表示该整数的倒数,如图1分别表示1/5,1/8,1/10和1/15。而对于一些特殊分数则构造了若干特殊符号表示,如图2则分别表示1/2和2/3。
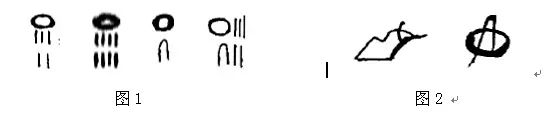
在古埃及人眼中,数字基本计算单位是1。令人称奇的是,他们却会使用2/3。对于一般分数(2/3除外),古埃及人均分解为单位分数再进行计算。这些均记载于古埃及纸草书。古埃及人用尼罗河中的一种草纤维制造出纸张,可在其上书写记录。莱因德纸草书就是其中一部数学著作,记有大量关于分数的计算问题。如,一个量,其2/3、1/2和1/7,加起来为33。这个量是多少?
纸草书是由书记员所写。古埃及的书记员是个崇高职业,他们会写字,能够进行数学计算,特别是懂得分数者,甚至扮演着创造奇迹的魔术师角色。故“知识就是力量”的社会规则,从古埃及就遵循和践行着。
2.中国古代的分数表示
中国关于分数概念的记载可追溯至商代(公元前12世纪前后),而在晚周铜器铭文中已出现了关于分数的叙述。因古人常略去“几分之几”的“之”字,故把3/5读作“五分三”。在公元前3世纪的《考工记》中,谈及车轮制作时,写有“十分寸之一为一枚”之句,其意为十分之一寸为一分。
由于我国古代的计算工具为算筹,故而未形成系列运算符号,运算一般表现为等式变换。在筹式中已有明确的分数表示法:商数置于上方,实(被除数,可看作分子)位列中间,法(除数,可看作分母)在最下方,运算结果中的实可能有余数,则视其为带分数。如图3表示:商64,实38,法583,相当于带分数(64×38)/583。这种分数表示方法和现代分子在上、分母在下的记法相同。再如23/7,其运算结果如图4。
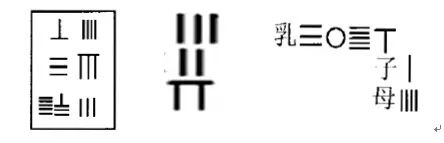
图3 图4 图5
在我国经典数学著作《九章算术》的“方田”章中,给出了完整的分数加、减、乘、除以及约分和通分运算法则。如第5题:今有十八分之十二,问约之得几何。再如第7题:今有三分之一,五分之二,问合之得几何。
《九章算术》中定义分数为:实如法而一。不满法者,以法命之。其大意为,被除数除以除数,若除不尽,就得到了一个分数。“命之”就是“命分”,我国古代把分数称之“命分”。
对于中国古代的分数表示法,英国科学史家李约瑟(J. T. M. Needham,1900-1995)曾赞誉道:分子和分母在运算前称之“子和母”,而在运算中称之“实和法”。用“儿子”表示分子和用“母亲”表示分母很有启发意义。这表明中国古人所想象的真分数,就是下面的数字较大,犹如怀孕的母亲一样。性(阴与阳)的差别使他们想到,除一个数与乘以其倒数是等效的。
南宋数学家秦九韶(1209-1262)在其《数书九章》中,独创了分数的另一种表示方法。如图5表示乳香重(3056×1)/4斤,其在算筹中明确标明了“子”和“母”的位置。
3.分数线的创立
在阿拉伯民族眼中,数学是智慧的母亲。为了表现慈母的端庄、秀丽,中国人应用竖行表示分数,然而这似乎还缺少一种内在美,故便在分子、分母之间添加了一条横线。这条美丽的线段不是分隔母子的沟壑,而是连接母子的彩带。
关于分数线的记载,最早见于阿拉伯数学家花拉子米(Mohammed ibn musa Al-khowarizmi,783-850)的著作《还原与对消计算概要》(代数学),他是从除法角度引进分数线的,他把“”记成3/5,表示3除以5。
花拉子米用代数方式处理了线性方程组与二次方程,第一次给出了一元二次方程的一般代数解法及几何证明,同时引进了移项、合并同类项等运算。约1140年该著作被英国数学家罗伯特(Robert of Chester)译成拉丁文,作为标准的数学课本在欧洲使用了数百年,引发了16世纪意大利代数方程求解方面的突破。花拉子米的另一部著作《印度计算法》(Algoritmi de numero indorum)系统介绍了印度数码和十进制记数法,以及相应的计算方法。该书传播到欧洲后影响很大,乃至后来称“印度数码”为“阿拉伯数码”。

意大利数学家斐波那契(Leonardo Fibonacci,1170-1250)把分数线带到了欧洲。斐波那契早年随其父在北非,师从阿拉伯数学家学习算学,后又游历到地中海沿岸诸国,回意大利后写成《算经》。该书内容涉及整数和分数计算方法,系统介绍了印度-阿拉伯数码,对改变欧洲数学现状产生了较大影响。
如同负数难以理解一样,欧洲人最初也不接受分数。直到15世纪后才逐步形成现代分数算法。最典型的是,德国数学家鲁多夫(C.Rudolff,1500-1545)于1530所编著的数学习题集,其中应用了分数线,并给出分数计算方法。

分数线的历史演进过程蕴含着数学的美妙与神奇。数学思想的实质是不可比拟的永久性和万能性及其对时间和文化背景的独立性。现今“数学”术语对应着英文单词mathematics,然而该词中文译法一直存在着分歧,直到1939年8月当时的教育部发文通令全国一律将英文mathematics译为“数学”。这是现代汉语数学词汇中唯一由行政手段规定的术语。对于具有数千年数学历史的中国来说,这似乎有点不可思议。事实上,所有知识皆为历史文化,所有科学皆应用数学工具,所有数学符号皆追求简洁。随着数学科学的进一步发展,人们自然需要追溯很多问题的来龙去脉,以便更好的预测未来。















