全库存（Safety Stock，SS）也称安全存储量，又称保险库存，是指为了防止不确定性因素（如大量突发性订货、交货期突然延期、临时用量增加、交货误期等特殊原因）而预计的保险储备量（缓冲库存）。

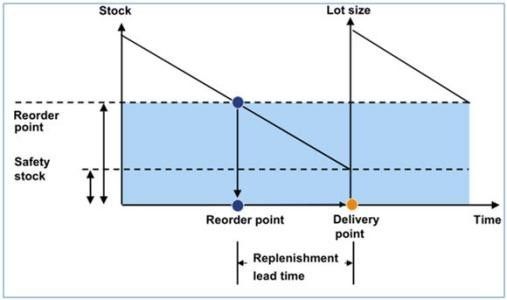
线性需求的安全库存：

最高库存量(成品)=最高日生产量×最短交付天数+安全系数/天

最低库存量(成品)=最低日生产量×最长交付天数+安全系数/天

最大库存量=平均日销售量×最高库存天数

最低库存量=安全库存+采购提前期内的消耗量

最低库存量=日销售量*到货天数+安全系数/天

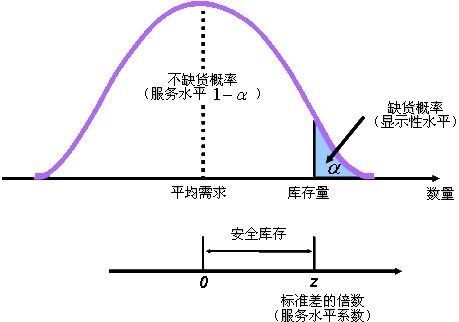
安全库存量的大小，主要由顾客服务水平（或订货满足）来决定。所谓顾客服务水平，就是指对顾客需求情况的满足程度，公式表示如下：

顾客服务水平 (5%) ＝年缺货次数 / 年订货次数

顾客服务水平（或订货满足率）越高，说明缺货发生的情况越少，从而缺货成本就较小，但因增加了安全库存量，导致库存的持有成本上升；而顾客服务水平较低，说明缺货发生的情况较多，缺货成本较高，安全库存量水平较低，库存持有成本较小。因而必须综合考虑顾客服务水平、缺货成本和库存持有成本三者之间的关系，最后确定一个合理的安全库存量。
对于安全库存量的计算，将借助于数量统计方面的知识，对顾客需求量的变化和提前期的变化作为一些基本的假设，从而在顾客需求发生变化、提前期发生变化以及两者同时发生变化的情况下，分别求出各自的安全库存量。

1. 需求发生变化，提前期为固定常数的情形

先假设需求的变化情况符合正态分布，由于提前期是固定的数值，因而我们可以直接求出在提前期的需求分布的均值和标准差。或者可以通过直接的期望预测，以过去提前期内的需求情况为依据，从而确定需求的期望均值和标准差。这种方法的优点是能够让人容易理解。
当提前期内的需求状况的均值和标准差一旦被确定，利用下面的公式可获得安全库存量 SS 。

SS=Z* SQRT(L) * STD
其中： STD --- 在提前期内，需求的标准方差；
Ｌ --- 提前期的长短；
Z   --- 一定顾客服务水平需求化的安全系数 ( 见下表 )

顾客服务水平及安全系数表
顾客服务水平 (%) 安全系数 z 顾客服务水平 (%) 安全系数 z
100.00          3.09             96.00      1.75
99.99           3.08             95.00      1.65
99.87           3.00             90.00      1.80
99.20           2.40              85.00     1.04
99.00           2.33             84.00      1.00
98.00           2.05             80.00      0.84
97.70          2.00              75.00     0.68
97.00           1.88

例：
某饭店的啤酒平均日需求量为 10 加仑，并且啤酒需求情况服从标准方差是 2 加仑 / 天的正态分布，如果提前期是固定的常数 6 天，试问满足 95% 的顾客满意的安全库存存量的大小？
解：由题意知：
STD ＝ 2 加仑 / 天，Ｌ＝ 6 天，Ｆ (Z) ＝ 95 ％，则 Z=1.65,
从而： SS=Z*SQRT(L) * STD ＝ 1.65*2.* SQRT(6) ＝ 8.08
即在满足 95% 的顾客满意度的情况下，安全库存量是 8.08 加仑。

2. 提前期发生变化，需求为固定常数的情形

如果提前期内的顾客需求情况是确定的常数，而提前期的长短是随机变化的，在这种情况下： SS 为

SS=Z* STD2 * d
其中： STD2 --- 提前期的标准差；
Z   ---- 一定顾客服务水平需求化的安全系数；
d-  --- 提前期内的日需求量；

例：
如果在上例中，啤酒的日需求量为固定的常数 10 加仑，提前期是随机变化的，而且服务均值为 6 天、标准方差为 1.5 的正态分的，试确定 95 ％的顾客满意度下的安全库存量。
解：由题意知：＝ 1.5 天， d ＝ 10 加仑 / 天，Ｆ (Z) ＝ 95 ％，则 Z=1.65 ，
从而： SS=Z* STD2 * d =1.65*10.*1.5=24.75
即在满足 95 ％的顾客满意度的情况下，安全库存量是 24.75 加仑。

3. 需求情况和提前期都是随机变化的情形

在多数情况下，提前期和需求都是随机变化的，此时，我们假设顾客的需求和提前期是相互独立的，则 SS 为

SS=Z * SQRT(STD*STD*L + STD2*STD2*D*D)
其中： Z---- 一定顾客服务水平下的安全系数；
STD2--- 提前期的标准差；
STD--- 在提前期内，需求的标准方差；
D---- 提前期内的平均日需求量；
L--- 平均提前期水平；

例：
如果在上例中，日需求量和提前期是相互独立的，而且它们的变化均严格满足正态分布，日需求量满足均值为 10 加仑、标准方差为 2 加仑的正态分布，提前期满足均值为 6 天、标准方差为 1.5 天的正态分布，试确定 95 ％的顾客满意度下的安全库存量。
解：由题意知： STD ＝ 2 加仑， STD2 ＝ 1.5 天， D ＝ 10 加仑 / 天， L ＝ 6 天，Ｆ (Z) ＝ 95 ％，则 Z=1.65 ，从而： SS=1.65*SQRT(2*2*6 +1.5*1.5*10*10) ＝ 26.04
即在满足 95 ％的顾客满意度的情况下，安全库存量是 26.04 加仑。

KPI指标：

KPI 指标			指标定义 / 计算公式	考核部门	被考核部门	数据来源
营运流程	供应链	供应商按时交付率	按时交付次数 / 总的订单次数
		原料合格率