【老顾将于5月9号,北京时间晚8点,于Games Webinar 讲解“几何观点下的对抗生成网络”,敬请参加,欢迎批评指正。】
【欢迎广大同学申请哈佛大学AI博士后职位,有意者请和老顾直接联系,[email protected]。】
艺术家们往往比常人更加敏感锐利,更能洞察庸常生活中的各种荒谬,并且更加激情澎湃。他们任凭想象力恣肆汪洋,用大胆直观的艺术形式来解释深邃的哲学内涵。很多杰出的“荒谬艺术”作品触目惊心,振聋发聩,令人无限深思。尤为奇妙的是,这些作品所表达的思想居然可以用严密的数学来描述,并且在现代科技的一些领域中,起到了关键的作用。同时,很多非常深奥晦涩的数学理论,在艺术表现形式下,变得直观易懂,直指人心。
埃舍尔(
Maurits Cornelis Escher
, 1898-1972)的很多作品脍炙人口,发人深省,于荒谬中见真理。

图1. Drawing Hands, Escher 1948.
埃舍尔的《绘画中的双手》(图1)描述了两只手彼此勾画,本来是纸面上的图画,跃然跳出纸面成为真实的双手,而衣袖和小臂依然停留在纸面之上。其实这幅图画表达了这样一个理念:虚拟的思想可以改变现实。这幅图非常恰切地描述了发生在金融市场上的情形,例如Token经济,虚拟货币。人们共同的信念塑造了经济的事实。当然,社会现实也反过来影响人们的信念。

图2. Print Gallery. Escher 1956.
埃舍尔的《画廊》(图2)更为抽象费解,在画廊中,一位青年在观赏墙壁上的一幅画,画中有一条大河,在河对岸有一座画廊;
在画廊
中,一位青年在观赏墙壁上的一幅画,
画中有一条大河,在河对岸有
一座画廊
......《画廊》描述了一个无限递归的结构,第一重结构描述了现实,第二重结构是一幅画,因而是虚拟结构,第三重结构是第二重结构中的一幅画,以此类推,直至无穷。这幅画天才地混淆了现实与虚拟,画中的画廊“流出”画面成为现实中的画廊。这幅画实际应用了曲面的共形变换,变换前的“正常”画面应该如(图3)所示。

图3. 变换前的《画廊》。

图4. Escher变换。
我们用图4来解释埃舍尔变换。左帧是老顾的办公室,桌子上放置了一个画框,里面贴了一张办公室的照片。照片的内部,有着一个画框,里面嵌套着第三级的画框......所有的画框交集是一个中心点,经过相似变换,我们可以将整个办公室的图像缩入到画框之中。这种相似变换构成一个群,整个平面去掉中心点,模掉这个变换群,商空间为一个拓扑轮胎曲面(torus),去心平面是轮胎曲面的覆盖空间。我们将轮胎曲面共形映射到自身,这一自映射诱导轮胎曲面的覆盖空间的自映射,其像为右帧图片。左帧封闭的画框被映射为右帧的无穷螺旋线,左帧现实和虚拟的分界线被打破,在右帧中现实和虚拟混为一谈。由于映射是共形的,局部形状被保持。

图5. Ascending and Descending 1960.
埃舍尔的另一杰作是《上升和下降》(图5),画中两队士兵在楼顶阶梯上迎面行进,左队士兵在不停地攀爬,右队的士兵在不停地下行,循环往复,永无止境。在现实生活中,所有的攀爬过程都会达到顶点,然后就是下降。这幅图局部看逼真合理,全局看却是无比荒谬,违背物理常识。这种局部合理,全局荒谬的现象在社会现实中、历史长河中比比皆是。
在很多工程领域,这种现象非常普遍,人们经常需要构造某种结构,局部非常容易构造,但是当从局部推广到全局,就会遇到难以意料的困难。例如几何辅助设计领域,局部构造样条曲面非常容易,但是构造覆盖整个曲面的全局光滑样条却具有本质困难;再如网格生成领域,局部构造规则化四边形网格非常简单,但是整个曲面四边形网格的自动生成非常困难。在数学中,在紧黎曼面的一个邻域上构造全纯函数非常容易,但是整个曲面上的全纯函数只能为常数。所有这些现象都表明某种全局存在性的内在障碍,对于这种
全局障碍
、这种
局部和整体的内在关系
的
精确描述是拓扑学的核心问题之一。目前最为普适的理论当属
层的上同调理论
。
将埃舍尔的《上升和下降》加以简化,取其精髓,构造著名的不可能模型-tribar,如图6左帧所示。这一模型局部看非常合理,但是整体物理不可实现。我们下面用层的上同调来加以解释,由此我们看到上同调的真意。
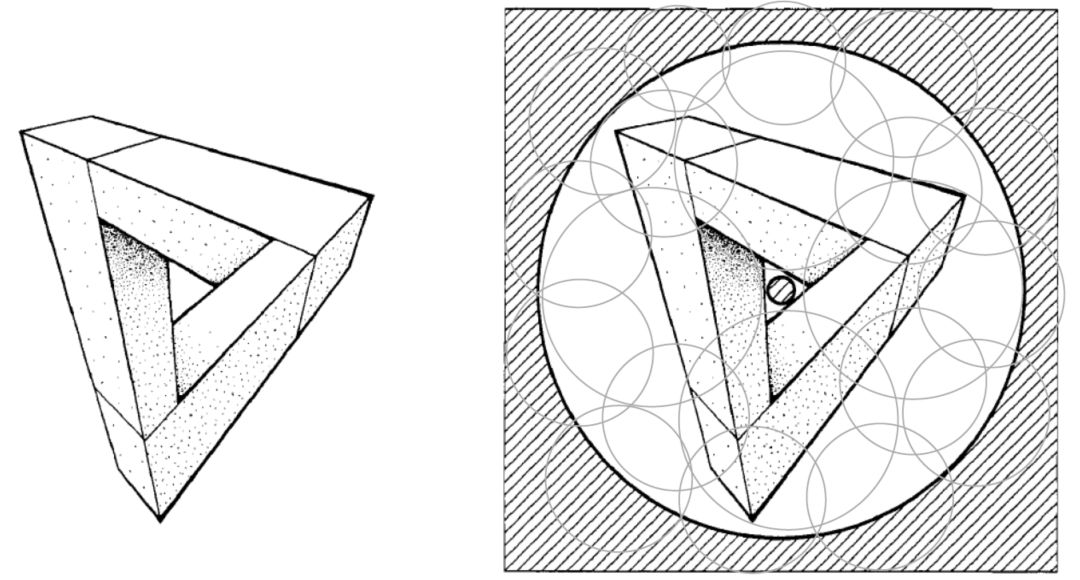
图6. tribar模型,及其开覆盖。
Cech 复形
如图6右帧所示,我们去掉Tribar的背景,tribar被容纳于一个拓扑环带
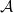 之中。然后,我们找到一族开圆盘
之中。然后,我们找到一族开圆盘
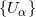 ,构成环带的有限覆盖,即
,构成环带的有限覆盖,即
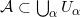 ;同时对于任意一点,覆盖此点的开圆盘有限。
;同时对于任意一点,覆盖此点的开圆盘有限。
我们为有限开覆盖
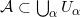 构造所谓的Cech复形(complex)
构造所谓的Cech复形(complex)
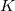 :
:
-
对每个开集
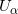 ,构造一个0维的顶点
,构造一个0维的顶点
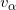 ;
;
-
如果两个集合交集
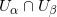 非空,加入一条1维的边
非空,加入一条1维的边
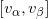 ;
;
-
如果三个集合交集
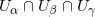 非空,加入一个2维的面
非空,加入一个2维的面
 ;
;
-
如果k个集合交集
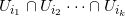 非空,加入
一个k维的单形(simplex)
非空,加入
一个k维的单形(simplex)
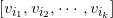 。
。
在Cech复形上,我们定义边缘算子:
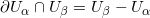 ,
,
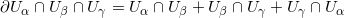 ,等等。我们用
,等等。我们用
 和
和
 表示单形,
表示单形,
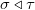 来表示
来表示
 包含在
包含在
 的闭包里,
的闭包里,
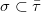 ,例如
,例如
 是
是
 的一个面。
的一个面。
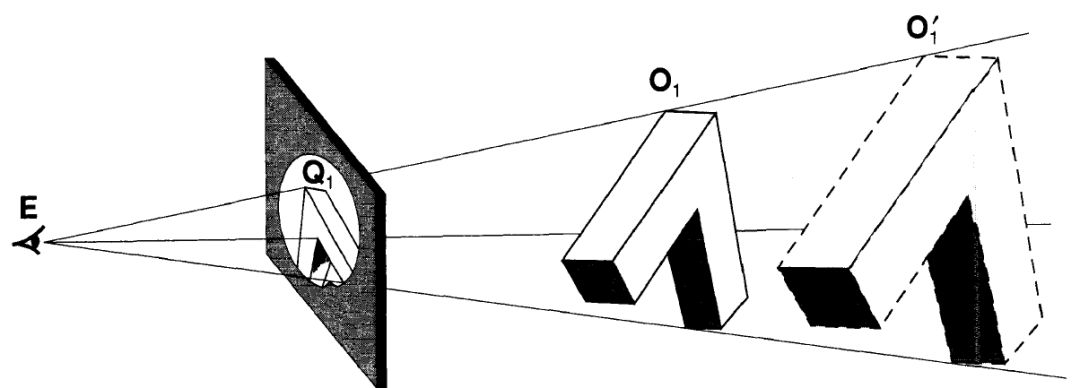
图7. 局部观察的歧义性,表达为一个位似(三维相似)变换群。
胞腔层
如图7所示,我们透过每个开圆盘去观察,看到整个物体的一部分信息。从三维到二维的投影映射,使得对于三维深度信息的推断具有歧义性。如图,从
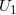 中观察,物体
中观察,物体
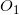 和
和
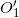 彼此相位似,
彼此相位似,
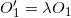 ,它们的投影同为
,它们的投影同为
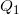 ,所有的位似变换构成一个阿贝尔群
,所有的位似变换构成一个阿贝尔群
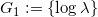 ,每个元素是一个位似变换,由
,每个元素是一个位似变换,由
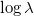 来表示,阿贝尔群为加法群。对于开覆盖中的所有开圆盘
来表示,阿贝尔群为加法群。对于开覆盖中的所有开圆盘
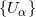 ,我们都如此定义了位似变换(三维中的相似变换)群
,我们都如此定义了位似变换(三维中的相似变换)群
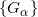 。每条边
。每条边
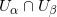 上可以类似定义相应的体似变换群
上可以类似定义相应的体似变换群
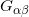 ;每个面
;每个面
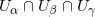 上类似定义相应的体似变换群
上类似定义相应的体似变换群
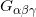 ,等等。
,等等。
Cech复形
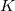 的每个单形上都配有一个阿贝尔群,这些群之间存在同态映射:如果
的每个单形上都配有一个阿贝尔群,这些群之间存在同态映射:如果
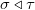 则存在同态
则存在同态
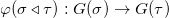 。同态满足复合律:如果
。同态满足复合律:如果
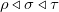 ,则
,则
 。
。
层的上同调
这些阿贝尔群和群同态构成了Cech复形上的胞腔层(Cellular Sheaf),记成
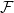 。为了统一符号,我们记群
。为了统一符号,我们记群
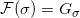 ,群同态
,群同态
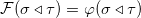 。层
。层
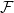 的一个n维上链(n-形式)
的一个n维上链(n-形式)
 就是为K的每一个n维单形
就是为K的每一个n维单形
 指定一个元素
指定一个元素
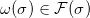 。所有的n维上链构成一个空间,所谓的n维上链空间
。所有的n维上链构成一个空间,所谓的n维上链空间
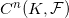 。我们可以定义上链空间
。我们可以定义上链空间
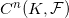 为所有n维单形
为所有n维单形
 上的阿贝尔群
上的阿贝尔群
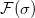 的积,
的积,
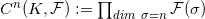 。由此得到上链复形:
。由此得到上链复形:
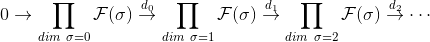
这里上边缘算子
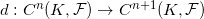 定义为
定义为
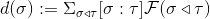 .
.
这里
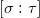 是
是
 和
和
 的关联系数。如果一个n维上链
(n-形式
)
的关联系数。如果一个n维上链
(n-形式
)
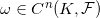 满足
满足
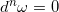 ,则我们说
,则我们说
 是一个n维闭形式;如果存在一个(n-1)维形式
是一个n维闭形式;如果存在一个(n-1)维形式
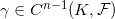 ,满足
,满足
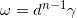 ,则我们说
,则我们说
 是一个n维恰当形式。根据定义,我们容易看出
是一个n维恰当形式。根据定义,我们容易看出
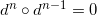 ,即恰当形式必为闭形式;但反之,闭形式未必是恰当形式;两者的差别就是上同调群。
,即恰当形式必为闭形式;但反之,闭形式未必是恰当形式;两者的差别就是上同调群。
由此层的上同调群定义为:
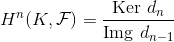 .
.
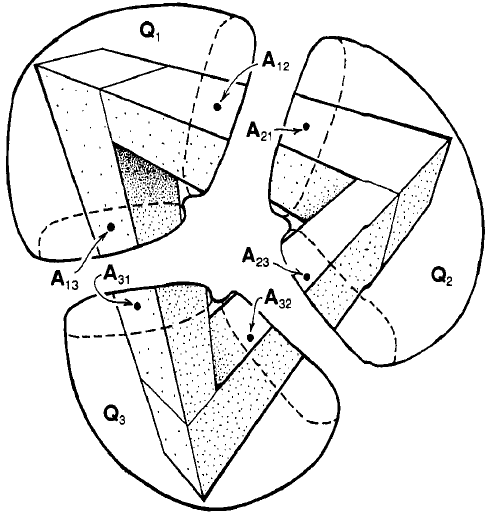
图8. 局部相容性。
局部-全局一致性
局部观察到数据的全局一致性由层的上同调来刻画。如图8所示,我们从不同的开集观察物体。从
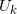 中观察得到图像为
中观察得到图像为
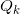 ,
,
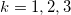 。假设存在一个物理真实的物体,在每个
。假设存在一个物理真实的物体,在每个
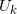 中
的位似系数为
中
的位似系数为
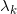 ,由此我们得到0-形式,
,由此我们得到0-形式,
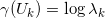 。图中,
。图中,
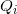 中的点
中的点
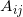 和
和
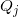 中的点
中的点
 对应着物体上的同一点,我们在
对应着物体上的同一点,我们在
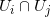 上定义此点的位似系数之比,由此得到1-形式
上定义此点的位似系数之比,由此得到1-形式
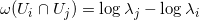 。由以上构造,我们有
。由以上构造,我们有
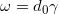 。我们在考虑三个开集相交的情形,
。我们在考虑三个开集相交的情形,
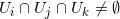 , 那么
, 那么
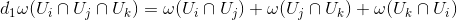
更进一步,由于
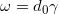 ,上式等于
,上式等于
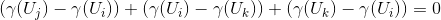 .
.
在实际情形中,在每个开集
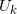 中直接确定位似系数
中直接确定位似系数
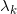 非常困难,判断两个开集交集
非常困难,判断两个开集交集
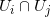 中位似系数的差异
中位似系数的差异
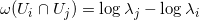 相对容易。局部合理等价于
相对容易。局部合理等价于
 是闭形式,
是闭形式,
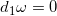 ;全局合理等价于
;全局合理等价于
 是恰当形式,
是恰当形式,
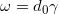 。在Cech复形中,如果
。在Cech复形中,如果
 是闭形式,但是非恰当形式,则
是闭形式,但是非恰当形式,则
 在任意能够缩成点的环路上积分都是0,但是在不能缩成点的环路上积分非0;如果
在任意能够缩成点的环路上积分都是0,但是在不能缩成点的环路上积分非0;如果
 是恰当形式,则
是恰当形式,则
 在任意环路上积分都为0。
在任意环路上积分都为0。
但我们将注意力集中在图8中的三个局部图像时,我们实际在判断
 是否是闭形式;当我们拉开距离,全局审视整个图像时,我们在判断
是否是闭形式;当我们拉开距离,全局审视整个图像时,我们在判断















