转载自:自然语言处理与机器学习
供稿人:忆臻
在我们了解过神经网络的人中,都了解神经网络一个有很常见的训练方法,BP训练算法.通过BP算法,我们可以不断的训练网络,最终使得网络可以无限的逼近一种我们想要拟合的函数,最终训练好的网络它既能在训练集上表现好,也能在测试集上表现不错!
那么BP算法具体是什么呢?为什么通过BP算法,我们就可以一步一步的走向最优值(即使有可能是局部最优,不是全局最优,我们也可以通过其它的方法也达到全局最优),有没有一些什么数学原理在里面支撑呢?
这几天梳理了一下这方面的知识点,写下来,一是为了记录,二也可以分享给大家,防止理解错误,一起学习交流.
BP算法具体是什么,可以参考我上篇文章推送(详细的将BP过程走了一遍,加深理解
通俗理解神经网络BP反向传播算法
)。
那么下面解决这个问题,为什么通过BP算法,就可以一步一步的走向更好的结果.
首先我们从神经网络的运行原理来看,假如现在有下面这个简单的网络,如图:
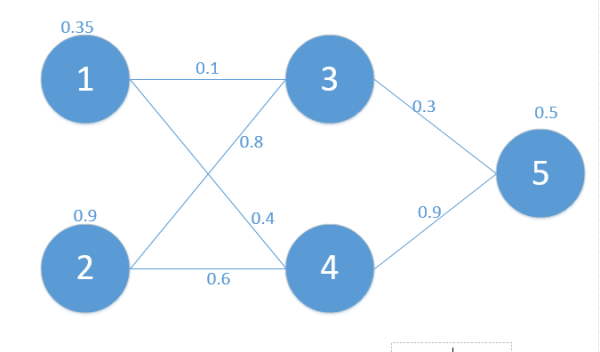
我们定义符号说明如下:
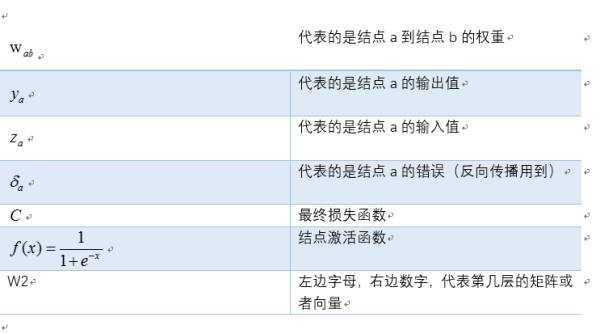
则我们正向传播一次可以得到下面公式:
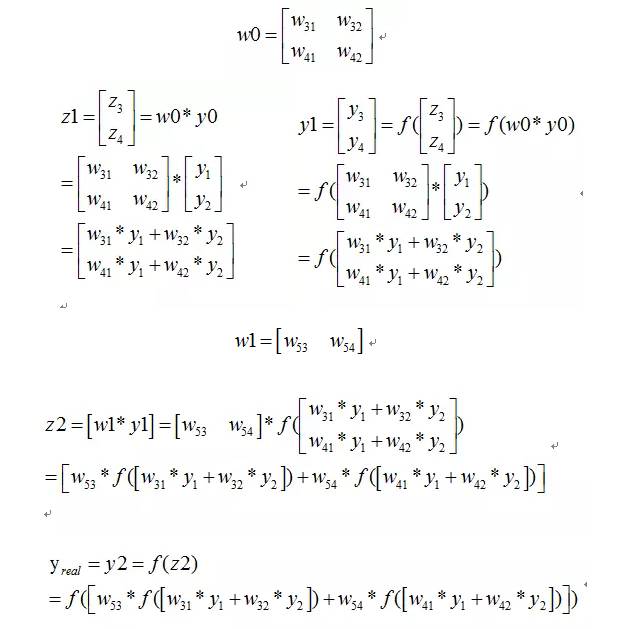
如果损失函数C定义为
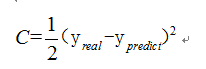
那么我们希望训练出来的网络预测出来的值和真实的值越接近越好.
我们先暂时不管SGD这种方法(感兴趣的可以参考我的这篇文章
详解梯度下降法的三种形式BGD,SGD以及MBGD
),最暴力的我们希望对于一个训练数据,C能达到最小,而在C表达式中,我们可以把C表达式看做是所有w参数的函数,也就是求这个多元函数的最值问题.那么成功的将一个神经网络的问题引入到数学中最优化的路上了.
好,我们现在顺利的将一个神经网络要解决的事情转变为一个多元函数的最优化上面来了.
现在的问题是怎么修改w,来使得C越来越往最小值靠近呢.常见的方法我们可以采取梯度下降法(为什么梯度下降法中梯度的反方向是最快的方向,可以参考我的这篇文章
为什么梯度反方向是函数下降最快的方向?
).
可能到这还有点抽象,下面举一个特别简单的例子.
假如我们的网络非常简单,如下图(符号说明跟上面一样):
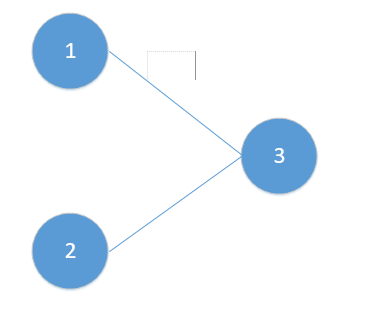
那么我们可以得到:
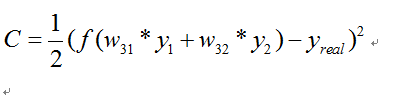
其中

只有w参数是未知的,那么C就可以看做是关于w的二元函数(二元函数的好处就是我们可以在三维坐标上将它可视化出来,便于理解~).图片来自于网络:
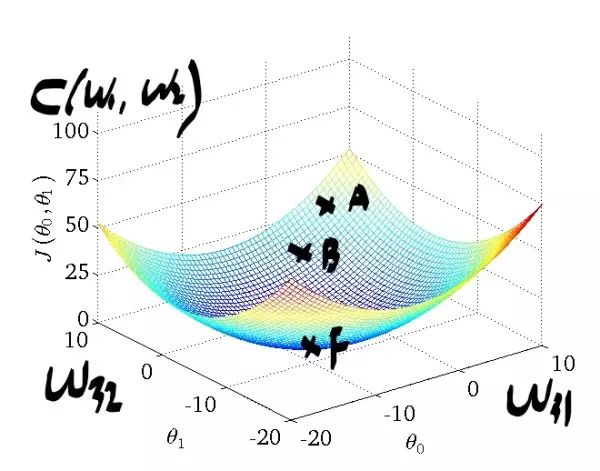
下面走一遍算法过程:
我们先开始随机初始化w参数,相当于我们可以在图上对应A点.
下面我们的目标是到达最低点F点,于是我们进行往梯度反方向进行移动,公式如下:
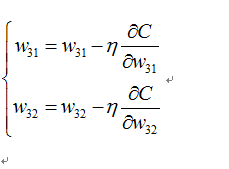
每走一步的步伐大小由前面的学习率决定,假如下一步到了B点,这样迭代下去,如果全局只有一个最优点的话,我们在迭代数次后,可以到达F点,从而解决我们的问题。
那么好了,上面我们给出二元函数这种简单例子,从分析到最后求出结果,我们能够直观可视化最后的步骤。
那么如果网络复杂后,变成多元函数的最优值求法原理是一模一样的!
到此,我结束了该文要讲的知识点了.欢迎各位同学指错交流~
在我学习的时候,我已经理解了上面的知识了,但是我在思考既然我最后已经得到一个关于w的多元函数了。
那么我为什么不直接对每一个w进行求偏导呢,然后直接进行更新即可,为什么神经网络的火起还需要bp算法的提出才复兴呢!
我的疑惑就是为什么不可以直接求偏导,而必须出现BP算法之后才使得神经网络如此的适用呢?下面给出我的思考和理解(欢迎交流~)
在神经网络中,由于激活函数的存在,很多时候我们在最后的代价函数的时候,包含w参数的代价函数并不是线性函数,比如最简单的
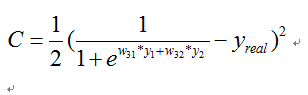
这个函数对w进行求导是无法得到解析解的,那么也就说明了无法直接求导的原因
2. 那么既然我们我们不能够直接求导,我们是否可以近似的求导呢?
比如可以利用
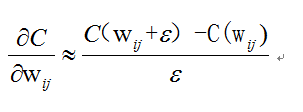
根据这个公式我们可以近似的求出对每个参数的导数,间距越小就越接近,那么为什么不可以这样,而必须等到BP算法提出来的时候呢?思考中.......
答:是因为计算机量的问题,假设我们的网络中有100万个权重,那么我们每一次算权重的偏导时候,都需要计算一遍改变值,而改变值必须要走一遍完整的正向传播.
那么对于每一个训练样例,我们需要100万零一次的正向传播(还有一次是需要算出C)。
而我们的BP算法求所有参数的偏导只需要一次反向传播即可,总共为俩次传播计时。
到这里我想已经解决了为什么不能够用近似的办法,因为速度太慢,计算复杂度太大了~每一次的传播,如果参数多的话,每次的矩阵运算量非常大,以前的机器速度根本无法承受~所以直到有了BP这个利器之后,加快了神经网络的应用速度.
以上仅个人理解,感谢德川的帮助!欢迎大家提出问题交流~







