作者：九三 来源：蒲公英
前段时间，对纯化水系统的电导率数据如何分析，进行描述和讨论；之后，就剩下对纯化水中微生物（需氧菌总数）数据怎么分析了。而纯化水系统的微生物控制又是十分关键的，应当如何分析呢？以下，是我的一些认识，或有不对，还是抛砖引玉吧。希望得到大家的批评指正。
首先，微生物数，从原理上，其是泊松分布，因为其是在单位时间/空间/重量内微生物的个数，所以，其应当是泊松分布。
其次，2015版《中国药典》四部的第386页“样品中微生物定量检验方法的验证”中，明确指出菌落数服从泊松分布。“微生物定量检验一般都涉及菌落计数。对计数结果进行数据处理时通常需要使用统计的方法。由于菌落计数服从泊松分布，因此采用泊松分布的统计方法对计数结果进行数据处理优于采用正态分布的统计方法。检验者往往习惯采用正态分布的统计方法，因此也可以通过对数转换或加1后开方的方法将原始数据转换为正态分布数据后再进行统计分析。两种统计方法都适用于微生物数据的统计分析。”
影响微生物检测结果的因素很多，所以，其误差较大；而出现异常结果时，查找问题时，也将更加困难，需要的专业知识也更全面，细节要求也更多，对整个检测体系要求较高，这一点，可以从2015版《中国药典》附录后，对微生物检测的要求之多，如下，可见一斑（第386页至第398页）。
9201 药品微生物检验替代方法验证指导原则
9202 非无菌产品微生物限度检查指导原则
9023 药品微生物实验室质量管理指导原则
9204 微生物鉴定指导原则
9205 药品洁净实验室监测和控制指导原则
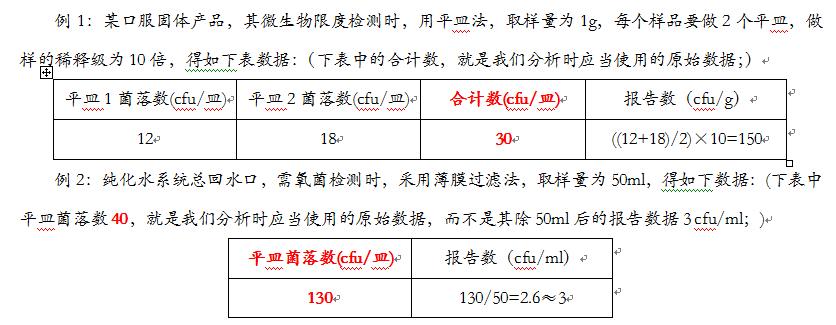
第三，微生物数据，具体分析时，一定要原始数据，不能是最后的报告数，因为报告数是以每ml/g计算的，这样说，不易理解，举例说明如下：
在马逢时主编的“六西格玛管理统计指南”中，对泊松分布的性质，是这样定义的，“从泊松分布的概念出发还可以看出下列性质，这就是均值λ的“可分性”，如果每罐稻米中的稗子数服从均值λ为6的泊松分布，那么很容易想到，如果以半罐作为一“小罐”，每小罐稻米中的稗子数应服从均值λ为3的泊松分布；若1000平米布的瑕疵点数的分布是λ＝25，瑕疵点数的分布是P(25),4平米可以缝制1套工作服，每套工作服的瑕疵点数的分布就应该是P(0.1)。这就是说，在单位（例如“罐”到“小罐”）换算时，泊松分布的性质不变，而且均值λ也可以做同样的换算，当然这里只限于被分割或被合并的总份数很少的情况才成立”。
上面提到的泊松分布的可分性，是指的泊松分布的总体均值λ的可分性，而不是，其原始数据的可分性，所以说，在对纯化水中需氧菌数，进行统计分析时，应当以其原始数据进行以泊松分布为基础的分析与判断，而不是以报告数（已经提前平均和修整过的数据）来进行分析。
下面，我们模拟一些数据做为总回水口需氧菌数据，来分析纯化水系统的微生物控制情况；模拟数据如下：
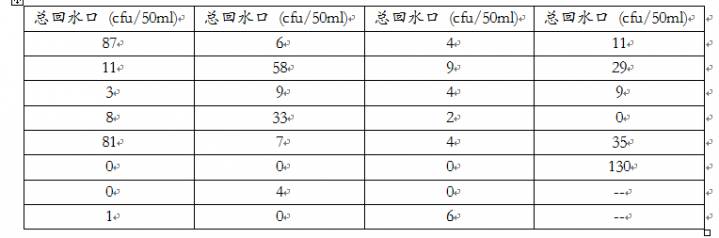
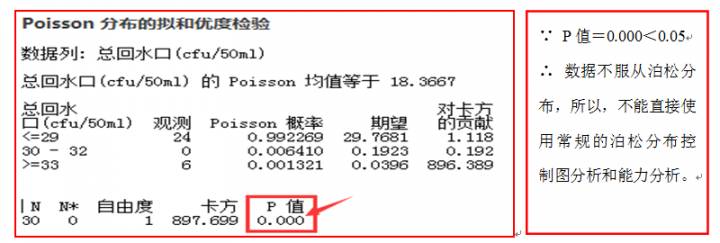
1、将总回水口需氧菌原始数据录入minitab 中，先做“统计/基本统计量/poisson分布的拟合优度检验”，看数据是否服从泊松分布，得如下结果：
2、如果数据是服从泊松分布的，那么可以直接使用minitab17中“C控制图和相应的poisson能力分析”即可，或者使用其协助功能更方便。这样的情况，就比较简单了，这里就不多做介绍；
3、多数情况下，数据恐怕是不服从泊松分布的，探求其原因，可能是纯化水系统，总会间隔一定的时间进行消毒处理，或还有检测系统存在测量误差问题。也希望，通过这篇文章，能引来讨论，继而找到问题的原因。
4、接下来，主要来说一说数据不服从泊松分布时，如何进行分析，从宏观上讲，纯化水中微生物不论经历怎样的干扰，其最终也是计点和计个数的事物，都应当是服从泊松分布的，所以，可以使用minitab中欠离散或过离散的泊松分布控制图和能力分析，进行相应分析，minitab17中有协助项，可以很便捷地进行分析，如下图所示：
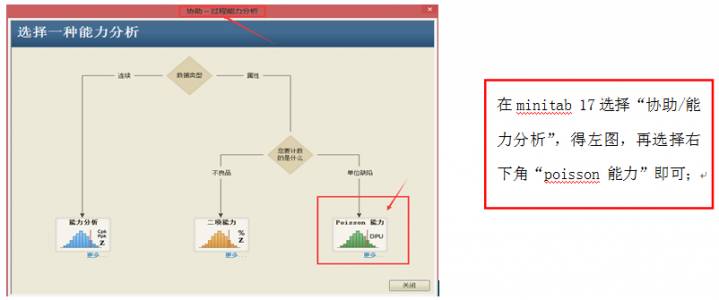
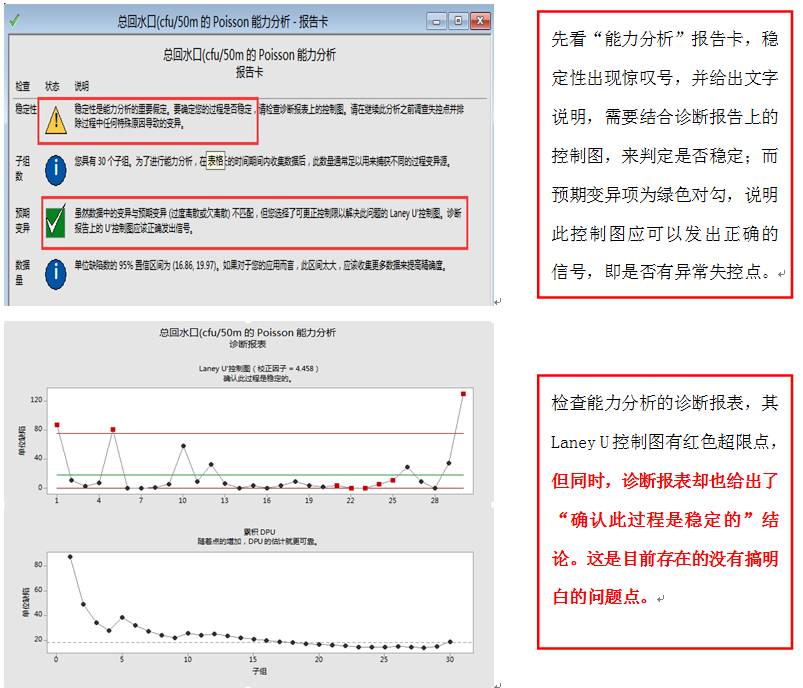
通过以上的统计分析，可到统计结论：以上模拟的纯化水回水的微生物控制能力很好；而从专业角度看，纯化水回水中的需氧菌数远低于标准，也可以说明本纯化水系统的微生物控制能力很好。
在这，还要说一点，数据统计分析的基础是数据，所以，数据要准确，要真实，这样，分析才有意义；同时，数据都是通过测量得到的，是测量必然会存在误差问题，误差不能过大，否则事物本来规律，可能就会被过大的误差所掩盖，过程中如果出现问题/不良趋势时，就可能因为过大的误差所干扰或掩盖了。
再者，我们要理性地看待和使用数据统计工具，并正确理解所得的统计结论；如果统计结论和专业结论一致，则最终结论也一致；如果统计结论和专业结论不一致时，则最终结论需根据专业知识而定。判断被试因素的有效性时，要求在统计上和专业上都有意义。
