大家都知道,开发一个营销模型真是够费心费力的:要对业务痛点有充分的了解,要清洗整合数据,要构建模型、试点应用……好在只要模型效果理想,甲方乙方总是皆大欢喜,付出的努力也获得了回报。
然而,有时候营销模型的持续性就不那么让人满意啦。比如实施的头几个月,营销效果还很理想,一线人员业绩提升、对模型赞不绝口;然而过了一段时间,营销效果就逐步下滑了……这到底是为什么呢?我们可以从营销方式上找找问题,也不妨回到模型本身,从样本到模型,做一次全面的检验。

问题一:样本是否大变样?(建模样本与试点样本是否差异过大)
举个例子,比如我们在建模时选入了“客户收入”这一变量用于预测,结果不久之后某行业形势大幅上涨,等到试点的时候,这些客户们的收入增长了50%……可以肯定地说,这时候模型效果一定会发生变化。
模型实施过程中,经济环境、银行策略等各种因素的变动,可能会对建模时选入的一些客户行为、属性变量产生影响,导致建模样本与试点样本差异过大,模型效果出现了“水土不服”。所以,我们首先需要对试点样本和建模样本进行对比分析,看看这份建模样本是不是已经过气了。这里主要介绍两个指数:
1. 系统稳定性指数:整体考察样本
系统稳定性指数(system stability index)从整体上考察了建模样本与营销试点样本之间的差异。由于模型的区分能力是建模样本中的信息量决定的,如果试点样本与建模样本之间已经出现了巨大偏差,就可能导致模型失灵;而系统稳定性指数就是
通过对建模样本和试点样本中客户营销成功概率的比较,来判断模型预测结果是否还稳定。具体计算方法如下:
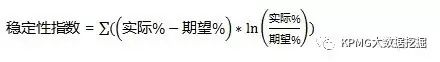
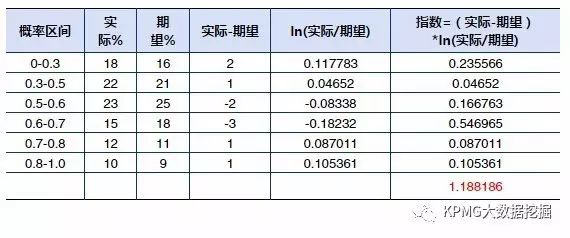
下表中展示了一个计算样例,数据仅为示例:
-
"概率区间"是指把依据建模样本得到的模型结果(客户营销成功概率)进行分组;
-
"实际%"是指试点样本中每一个概率区间的客户占总体的比例;
-
"期望%"则为建模样本中每一个概率区间的客户占总体的比例。
最终的系统稳定性指数
(表中红色部分)
就是各区间段指数的加总值,该值越小,模型就越稳定,表明试点样本的概率分布情况和建模样本中的情况越相似,可以预期模型在试点样本中的性能表现和建模样本中的性能表现会很接近。
一般来说,系统稳定性指数在0.1以下,我们认为样本分布间的差异不是很大,稳定性较高;0.1-0.25之间意味着样本分布发生了一定的变化,而0.25以上就意味着样本分布发生了较大的变化。
接下来,我们需要进一步通过变量稳定性指数,去发掘真正导致分布大幅变化的变量。
2. 变量稳定性指数:深入考察个体变量
系统稳定性指数可以从整体上检验模型,但具体到每个变量在两个时间段之间的变化情况,我们就需要引入变量稳定性指数了。即使系统稳定性指数尚可接受,对变量的细致考察也是必需的。
变量稳定性指数通过对建模样本和试点样本中变量取值分布的比较,来判断模型预测结果的预期稳定性。具体计算方法与系统稳定性指数类似,只是将概率区间转换成了该变量不同分布段的取值。
变量稳定性指数的计算过程可以看出变量的分布较建模时候的变化情况,如果出现变化较大的情况,该变量的权重就需要重新计算了。示例数据如下:
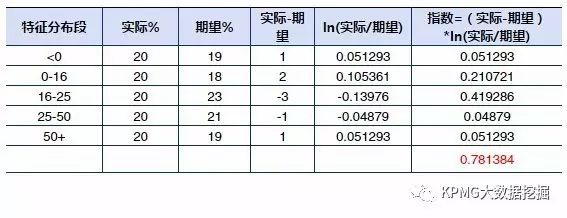
该指数的评价区间与系统稳定性指数相似。对每个入选变量都这样计算一下,就可以找出那些导致样本分布变化的变量了。
经过以上两个指标的考验,我们就可以确定样本是否出现问题,并相应地更新样本、调整权重等。
问题二:模型是否还有效?
除了样本可能出现的差异之外,我们还需要考察一下模型本身的表现水准。有时候,主观判断的模型营销效果其实并不能代表真实发生的情况,因此,应该从稳定性和准确性两个角度,客观判断模型是否还处于有效期。
前提:根据试点结果,我们可以知道本次试点客户最终是否购买了我的营销产品,也就是对应营销模型的响应变量y到底取值为1还是0。
1. 稳定性指标:模型性能稳定性指数















