姿态解算
姿态解算(attitude algorithm),是指把陀螺仪，加速度计, 罗盘等的数据融合在一起，得出飞行器的空中姿态，飞行器从陀螺仪器的三轴角速度通过四元数法得到俯仰，航偏，滚转角，这是快速解算，结合三轴地磁和三轴加速度得到漂移补偿和深度解算。
姿态的数学模型坐标系
姿态解算需要解决的是四轴飞行器和地球的相对姿态问题。地理坐标系是固定不变的，正北，正东，正上构成了坐标系的X，Y，Z轴用坐标系R表示，飞行器上固定一个坐标系用r表示，那么我们就可以适用欧拉角，四元数等来描述r和R的角位置关系。
姿态的数学表示
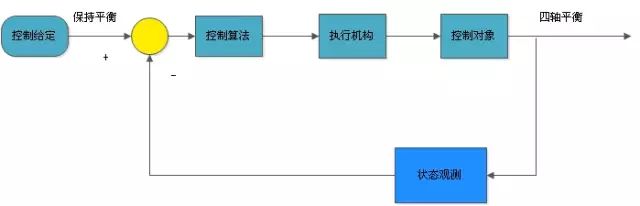
姿态有多种数学表示方式，常见的是四元数，欧拉角，矩阵和轴角。在四轴飞行器中使用到了四元数和欧拉角,姿态解算的核心在于旋转。姿态解算中使用四元数来保存飞行器的姿态，包括旋转和方位。在获得四元数之后，会将其转化为欧拉角，然后输入到姿态控制算法中。姿态控制算法的输入参数必须要是欧拉角。AD值是指MPU6050的陀螺仪和加速度值，3个维度的陀螺仪值和3个维度的加速度值，每个值为16位精度。AD值必须先转化为四元数，然后通过四元数转化为欧拉角。在四轴上控制流程如下图：
下面是用四元数表示飞行姿态的数学公式，从MPU6050中采集的数据经过下面的公式计算就可以转换成欧拉角，传给姿态PID控制器中进行姿态控制.
PID控制算法
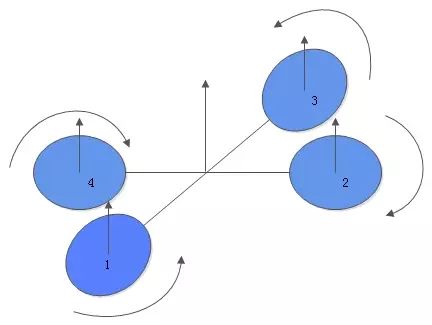
先简单说明下四轴飞行器是如何飞行的,四轴飞行器的螺旋桨与空气发生相对运动，产生了向上的升力，当升力大于四轴的重力时四轴就可以起飞了。四轴飞行器飞行过程中如何保持水平：我们先假设一种理想状况：四个电机的转速是完全相同的是不是我们控制四轴飞行器的四个电机保持同样的转速，当转速超过一个临界点时（升力刚好抵消重力）四轴就可以平稳的飞起来了呢？答案是否定的，由于四个电机转向相同，四轴会发生旋转。我们控制四轴电机1和电机3同向，电机2电机4反向，刚好抵消反扭矩，巧妙的实现了平衡, 但是实际上由于电机和螺旋浆本身的差异，造成我们无法做到四个电机产生相同的升力，这样飞行器起飞之后就会失去平衡。
PID控制器
PID控制器通过PID三个参数来对被控对象进行控制，是应用最广泛一种的控制器
比例(P)控制器
比例控制是一种最简单的控制方式。其控制器的输出与输入误差信号成比例关系。当仅有比例控制时系统输出存在稳态误差。
积分(I)控制器
在积分控制中，控制器的输出与输入误差信号的积分成正比关系。对一个自动控制系统，如果在进入稳态后存在稳态误差，则称这个控制系统是有稳态误差的 或简称有差系统（System with Steady-state Error）。为了消除稳态误差，在控制器中必须引入“积分项”。积分项对误差取决于时间的积分，随着时间的增加，积分项会增大。这样，即便误差很小，积 分项也会随着时间的增加而加大，它推动控制器的输出增大使稳态误差进一步减小，直到等于零。因此，比例+积分(PI)控制器，可以使系统在进入稳态后无稳态误差。
微分(D)控制器
微分调节就是偏差值的变化率。使用微分环节能够实现系统的超前控制。如果输入偏差值线性变化，则在调节器输出侧叠加一个恒定的调节量。大部分控制系统不需要调节微分时间。因为只有时间滞后的系统才需要附加这个参数。如果画蛇添足加上这个参数反而会使系统的控制受到影响。
四轴飞行器中的控制器
目前四轴飞行器中所使用的是增量是PD控制器，下面以ROLL方向为例
测得ROLL轴向偏差
偏差 = 目标期望角度 – 传感器实测角度
DIF_ANGLE.X = EXP_ANGLE.X - Q_ANGLE.Roll;
比例项计算
比例项输出 = 比例系数P * 偏差
Proportion = PID_Motor.P * DIF_ANGLE.x;
微分计算
微分输出 = 微分系数 × 角速度
整合结果
ROLL方向总控制量 = 比例项输出+微分量输出
电机输出
Motor[2] = (int16_t)(Thr - Pitch - Roll - Yaw ); //M3
Motor[0] = (int16_t)(Thr + Pitch + Roll - Yaw ); //M1
Motor[3] = (int16_t)(Thr - Pitch + Roll + Yaw ); //M4
Motor[1] = (int16_t)(Thr + Pitch - Roll + Yaw ); //M2
旋转规则
Roll方向旋转，则电机1电机2同侧出力，电机0电机3反向出力
Pitch方向旋转，则电机2电机3同侧出力，电机0电机1反向出力
Yaw方向旋转，则电机1电机3同侧出力，电机0电机2反向出力
源自：走近无人机
专注于机器人、无人机/车，工程师都关注的“机器人网”
