论文地址：https://arxiv.org/abs/1705.07038
本论文通过理论分析深度神经网络群体风险（population risk）的收敛行为和它的驻点（stationary point）与属性来研究深度学习的经验风险（empirical risk）全景图。对于 L 层的线性神经网络，我们证明其经验风险一致收敛到训练样本大小为 n、比率（rate）为
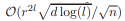的群体风险，其中 d 是总权重维度、r 是每一层权重的量级范围。然后，我们基于这一结果推导出经验风险的稳定性和泛化边界。此外，我们确立了经验风险梯度与群体风险梯度的收敛一致性。我们同样证明了经验风险和群体风险之间的非退化（non-degenerate）驻点和收敛的对应关系，这就描述了深度神经网络算法的全景图。此外，我们同样分析了用 Sigmoid 函数作为激活函数的深度非线性神经网络的特性。我们证明了深度非线性神经网络经验风险梯度的收敛行为和线性一样，并同时分析了其非退化驻点的性质。
据我们所知，该研究是第一次理论上描述深度学习算法全景图（landscape）的工作。此外，我们的研究结果为训练良好的深度学习算法提供了样本复杂度（sample complexity）。我们同样提供了神经网络深度 L、层级宽度、网络规模 d 和参数量级如何决定神经网络格局的理论理解。
简介
深度学习算法已经在很多领域取得了令人瞩目的成果，比如计算机视觉 [1, 2, 3]、自然语言处理 [4, 5] 和语音识别 [6, 7] 等等。然而，由于其高度非凸性和内在复杂性，我们对这些深度学习算法属性的理论理解依然落后于其实际成就。事实上，深度学习算法经常通过最小化经验性风险来学习其模型参数。因此我们致力于分析深度学习算法的经验风险全景图以更好地理解其实际表现。
正式地，我们考虑由 L 层网络 (L ≥ 2) 组成的深度神经网络模型，并通过最小化常用的平方损失函数（来自未知分布 D 的样本 
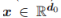）进行训练。理想情况是深度学习算法可通过最小化群体风险找到其最优参数 w∗。
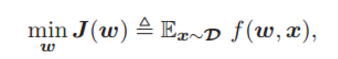
其中 w 是模型参数，
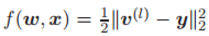
该方程为样本 x 服从分布 D 的平方损失函数。这里 v (l) 是第 l 层的输出，y 是样本 x 的目标输出。实际上，由于样本分布 D 经常未知，并且只有有限的训练样本 x(i)，以及来自 D 的
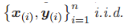，所以常常通过最小化经验风险以训练网络模型。
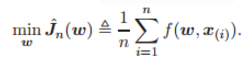
在这项工作中，通过将经验风险收敛到群体风险 J(w) 及其驻点和属性的分析，我们同时为多层线性和非线性神经网络描述了深度学习算法经验风险的全景图。
文献综述
到目前为止，只有少数理论可以解释深度学习，并且它们可大致被分为三类。
第一类旨在分析深度学习的训练误差。
第二类的工作 [13, 14, 9, 15] 致力于分析深度学习之中高度非凸性损失函数的损失曲面，如驻点的分布。
第三类是一些最近的工作，其试图把问题分解为更小的部分来试图降低分析难度。
然而，还没有分析深度学习算法经验风险全部格局的工作。
4. 深度线性神经网络的研究结果
我们首先证明了深度线性神经网络经验风险到群体风险的一致收敛性（uniform convergence）。基于该项证明，我们推导出了稳定性和泛化边界（generalization bounds）。随后，我们提出了经验梯度（empirical gradient）和群体梯度之间的一致性收敛保证，然后还分析了经验风险非退化驻点的性质。
在本论文的分析中，我们假定输入数据 x 服从τ^2 -sub-Gaussian 分布，同时如假设 1（Assumption 1）所述存在受限量级。
假设 1. 输入数据
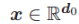，其均值为 0 且服从 τ^2 -sub-Gaussian 分布。因此 x 就满足
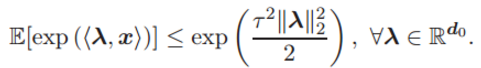
此外，x 的 L2 范数满足（x 的量级受限）：
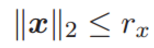
其中 rx 为正项通用常数。
4.1 一致性收敛、经验风险的稳定性和泛化性
定理 1 确定了深度线性神经网络经验风险的一致收敛性结果。
定理 1： 假定假设 1 中的输入数据 x 在深度神经网络中的激活函数是线性的。那么存在两个通用常数 cf ′ 和 cf，且满足：
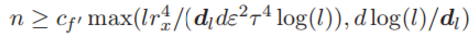
那么，就存在：
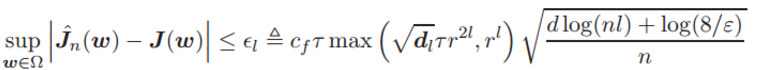
该不等式的置信度至少为 1 − ε。其中 l 为神经网络层级数量、n 为样本规模、dl 为最后一层的维度大小。
4.2 梯度的一致性收敛
在这一部分中，我们分析了深度线性神经网络的经验风险和群体风险的梯度收敛性。梯度收敛的结果对描绘神经网络算法的全景图十分有效。我们的结果展现在下面。
定理 2 ：假定假设 1 中的输入数据 x 在深度神经网络中的激活函数是线性的。经验风险梯度在 L2 范数（欧几里德范数）中收敛到群体风险梯度。特别地，若
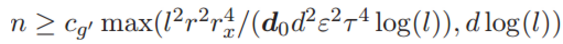
其中 cg' 为通用常数，那么存在通用常数 cg 满足：
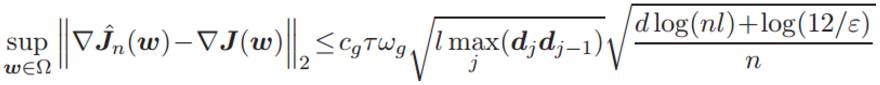
该不等式的置信度至少为 1 − ε，其中
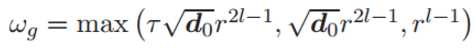
4.3 驻点的一致性收敛
这里我们分析了在优化深度学习算法经验风险时的驻点属性。为了简化起见，我们使用了几何性孤立（geometrically isolated）的非退化驻点，因此该驻点局部中是唯一的。
5 深度非线性神经网络的结果
在以上章节，我们分析了深度线性神经网络模型的经验风险优化全景图。在本节中，我们接着分析深度非线形神经网络，它采用了 sigmoid 激活函数并在实践之中更受欢迎。值得注意的是，我们的分析技巧也适用于其他三阶微分函数，比如 带有不同收敛率的 tanh 函数。这里我们假设输入数据是高斯变量（i.i.d. Gaussian variables）。
5.1 一致性收敛、经验风险的稳定性和泛化
本章节中，我们首先给出经验风险的一致收敛分析，接着分析其稳定性（Stability）和泛化。
定理 4. 假定输入样本 x 服从假设 2，并且深度神经网络的激活函数是 sigmoid 函数，那么如果
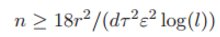
那么存在通用的常数 cy，满足：
该不等式的置信度至少为 1−ε，其中
5.2 梯度和驻点的一致性收敛
在这一部分中，我们分析了深度非线性神经网络经验风险的梯度收敛性质。
定理 5 假定输入样本 x 服从假设 2，并且深度神经网络中的激活函数为 sigmoid 函数。那么经验风险的梯度以 L2 范数（欧几里德范数）的方式一致收敛到群体风险的梯度。特别地，如果
其中 cy' 为常数，那么有：
该不等式的置信度至少为 1 − ε，其中 cy、 cd 和 cr 是在定理 4 中的相同参数。
6 证明概览
在该章节中，我们将简单介绍证明的过程，不过由于空间限制，定理 1 到 6、推论 1 到 2、还有技术引理在补充材料中展示。
7 结论
在这项工作中，我们提供了深度线性／非线性神经网络经验风险优化全景图的理论分析，包括一致性收敛、稳定性和经验风险本身的泛化及其梯度和驻点的属性。我们证明了经验风险到群体风险的收敛率为
。这些结果同样揭示了神经网络深度（层级数）l、网络大小及宽度对收敛率至关重要。我们也证明了权重参数的量级在收敛速度上也扮演着重要角色。事实上，我们建议使用小量级权重数。所有的结果与实践中广泛使用的网络架构相匹配。
更多有关GMIS 2017大会的内容，请点击「阅读原文」查看机器之心官网 GMIS 专题↓↓↓
