怪事年年有,今年特别多,黑娃教的高二·五班就遇到一件怪事。
有一天晚自习,黑娃在黑板上写了一道求定值的圆锥曲线问题,他叫学生先练习,打算第二天上午第一节来评讲,题目是这样的:
椭圆
的左、右顶点为
、
,过左焦点的直线与椭圆交于
,
两点,求证:
为定值.
第二天早上,黑娃走进教室一看,黑板上已经写着这个题的详细解答:
解:先由特殊情况确定定值.
当
轴时,
,
,
,
,
易知
下面证明
满足一般情况.
令
,
,直线
的方程为:
.
由
可得
.
上式显然成立,所以
黑娃仔细审查解答过程,心里暗暗叫好。不仅答案完全正确,而且解答结束时还对解题方法进行了归纳和提炼,附上几句解题口诀:
存在定值与定点,常规方法直接算;
特殊情况找结论,一般情况再验证;
可以化为恒成立,考问恒定啥条件。
“这是谁解答的?”黑娃有些惊喜、有些疑惑。
上课铃响了,黑娃问是谁写的答案,教室里无人应答,黑娃心想,可能担心答案有错不敢承认,于是说:“这种解法很好,答案完全正确,特别是最后几句解题口诀写得漂亮,有画龙点睛的作用,我们掌声欢迎这位同学上台给大家讲解思路。”同学们左顾右盼,依然没有人承认。黑娃见没人上台,猜想是一名腼腆的女生写的,胆子小不敢上台。于是就对黑板上的解答进行分析和讲解。
又是一次物理晚自习,老师在小黑板上写了一道习题,叫全班同学先练习,老师第二天上午来评讲,题目是这样的:
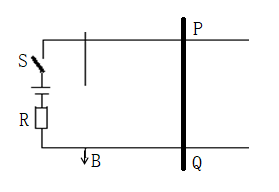
如图所示,水平放置的两平行金属导轨相距
,电源电动势
=6V,内阻不计,串联电阻 R=5
,匀强磁场方向竖直向下。开关 S 闭合后,横放在导轨上的金属棒
在磁场力的作用下由静止开始向右运动,金属棒与导轨间的滑动摩擦力
. 为使金属棒的运动速度
最大,磁感强度
为多少?此时
的最大值为多少?
第二天早上,物理老师走进教室一看,黑板上已经写着这个题的详细解答:
解:随着
的增大,感应电动势也增大,合电动势减小,
棒中的电流也减小,磁场力随之减小,当磁场力减小到与阻力相等时,
棒速度最大,此后将作匀速直线运动。
设匀强磁场的磁感强度为
,
棒上产生的感应电动势为:
电流为
.
棒受磁场力
当磁场力的大小等于阻力
时,棒受合力为零,作匀速直线运动,则
(把
看作变量,此式使我们联想到用判别式求值域的数学方法)
由
,得
所以,金属棒
最大速度
从而可得
老师审查了解答过程,觉得解题方法很好,特别是利用判别式求最大值这一招最精彩,将数学和物理的完美结合。他没有擦黑板,打算让学生上台讲解,想用学生的解答来激励学生,营造竞争场。等到上课时,老师问是谁写的答案,没有人应答,连续问了三次都无人应答,物理老师心想:高中生稳重、内敛,不像初中生那样爱表现,还是自己讲解吧。
办公室里,黑娃和物理老师谈及此事,大家觉得很奇怪,过去从未遇到这种情况,有老师怀疑班上隐藏着奇才。班主任建议,让黑娃再写一个很难的数学竞赛题试试,看看班上究竟有没有卧龙。
又到数学晚自习,黑娃在黑板上写了一个难度很大的 IMO 数学竞赛题,然后说:“大家先练习,明天上午我来评讲。”题目是这样的:
令
、
是一个正八边形的两个相对顶点,一只青蛙从
定开始跳动,除了
点外,从八边形中的其他每一个顶点都可以跳至与它相邻两顶点中的任何一个。当它跳到
点时就停止运动。设
为恰好经过
步跳动以后到达
点的所有可能线路的个数,求证:
(1)
;
(2)
第二天,黑娃、物理老师和班主任一大早来到学校,想看看有无奇迹发生,他们走进教室一看,被眼前的情景惊呆了,教室里没有一个学生,黑板上却写着详细解答:
解:设经过
步跳动以后到达各顶点的所有可能线路的个数为
.

由
,消去
可得:
易知:















