
也许,此时的你正被数学老师的作业压抑得喘不过气来,被函数、立体几何、线性回归折磨得只想放弃。
但你可能不知道,数学有他本身的美,数学的背后,有许多有趣的故事。
音乐家说
数学是世界上最和谐的音符。
植物学家说
世界上没有比数学更美的花朵。
美学家说
哪里有数学,哪里才有真正的美。
哲学家说
你可以不相信上帝,
但是你必需相信数学,
世界什么都在变,
唯有数学是永恒的。
可能你对以上的各种回答还不能产生共鸣,因为,正处于学生生涯的你(尤其是文科生),只想说:数学是我的噩梦!


英国学生 Rory Kirkman 在数学考试两次失败后,
把可恨的二次方程求根公式纹在了身上
我们真的那么讨厌数学吗?今天,就让我们来一次伟大的数学公式巡礼。如果在课堂上,老师告诉了你数学公式背后有这么多有趣的故事,你会爱上数学吗?
NO.1 世上最简单的公式

稍有数学阅历的人都有这样的直觉,凡是“简洁”的公式都会给人以美感。而 1+1=2,这是所有公式中最简单明了的一个了,我们只有把它的发明归功于上帝。

公式背后的故事:
尽管从远古起人们都心照不宣地知道 1+1=2,但直到1557年的某一天,这一等式才写成类似于我们今天的形式。也就是说等号这个每个等式中都有的成分直到16世纪才第一次出场亮相。
NO.2 毕达哥拉斯定理
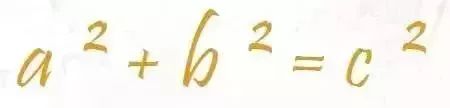
即勾股定理。“勾三股四弦五”,这一定理是如此地深入每一个地球人的心灵。它是人类早期发现并证明的重要数学定理之一(公元前约三千年的古巴比伦书版中就有记载),也是用代数思想解决几何问题的最重要的工具之一。勾股定理(毕达哥拉斯定理)约有400种证明方法,是数学定理中证明方法最多的定理之一。

公式背后的故事:
毕达哥拉斯是古希腊传统数学和哲学的创始人。以他的名字命名的学派是一个个人崇拜的秘密组织,鼓吹节欲、尊长和一夫一妻制。他认为,世界万物都是由数字统治的,他用数字推断人的命运,如奇数被认为与男性有关,而偶数与女性有关。他发现了称之为『完全数』的数字,也就是那些等于自己全部真因子之和的数字。比如:6(6=1+2+3)和 28(28=1+2+4+7+14)。已知的完全数共有47个,随着计算机发展速度的日益加快,每隔几年就会发现新的完全数。
NO.3 圆周率的发现
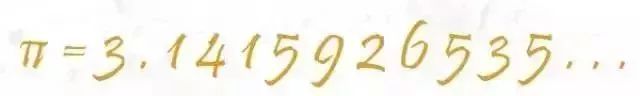
目前,人类已经能得到圆周率的10万亿位精度。不过现代科技领域使用的圆周率值,有十几位已经足够了。如果用35位精度的圆周率值,来计算一个能把太阳系包起来的圆的周长,误差还不到质子直径的百万分之一。现在的人计算圆周率,多数是为了验证计算机的计算能力,还有就是为了兴趣。

公式背后的故事——布丰投针实验:
在地板上画一系列间距为2厘米的平行线,然后把一根长度为1厘米的针扔在地板上。那么,这根针与地板上的线条相交的概率是多少呢?1733年,法国博物学家布丰第一次提出了这个问题。1777年,布丰自己解决了这个问题——这个概率值是1/π。
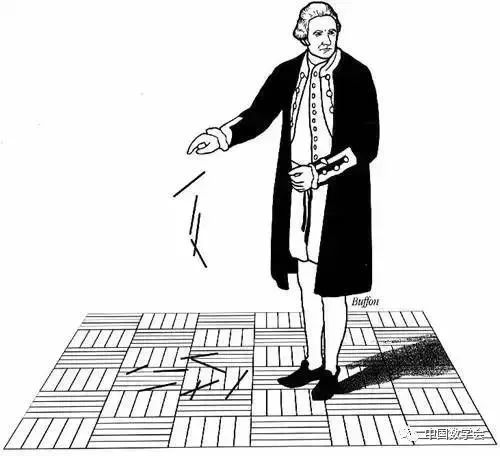
看到这个事实,阿基米德会目瞪口呆、刘徽会无语凝噎。所以,如果上帝创造了整数,而且他也创造了π,那或许上帝其实是一台计算机。
NO.4 费马最后的定理
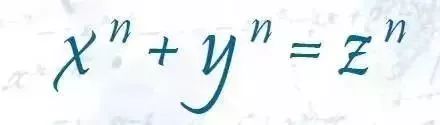
1637年的某一天,法国律师兼业余数学家费马,在一本书的空白处写下了下面一段话:
任何立方数都不可能写为两个立方数之和的形式,也没有任何四次方数可以写成另外两个四次方数的形式。普遍地说,任何二次以上的幂都不可能写成另外两个同次幂的形式。
即,当指数n大于2时,上述方程没有整数解。
在写下上面的猜想后,这个天生羞涩、沉默寡言的人却跟世界玩了一个恶作剧,他又写道:
对此我已经找到了一个真正绝妙的证明,但这里空白处太小,写不下。
然而,他怎料到,他随意写下的两句手记,却让350年间的无数数学家耗尽一生,也没能找到那个证明。直到1994年,英国人安德鲁·怀尔斯才证明了费马最后定理。


公式背后的故事:
德国人数学家沃尔夫斯凯尔因追求一位漂亮女性被拒绝,遂决定在午夜钟声响起时开枪自杀。他认真地安排好后事,写下遗嘱。他的高效率使得所有的事情略早于午夜的时限就办完了。为了消磨最后的几个小时,他到图书室翻阅数学书籍:一篇关于费马大定理证明的论文……他不知不觉拿起了笔,一行一行进行计算……
然后,天亮了。
沃尔夫斯凯尔为自己发现并改正了论文中的一个漏洞感到无比骄傲,原来的绝望和悲伤消失了,数学将他从死神身边唤回。
1908年,得享天年的沃尔夫斯凯尔写下了他新的遗嘱:他财产中的一大部分作为一个奖,规定奖给任何能证明费马大定理的人,奖金是10万马克,按现在的币值超过100万英镑。
这是他对那个挽救过其生命的盖世难题的报恩方式。
NO.5 微积分基本定理
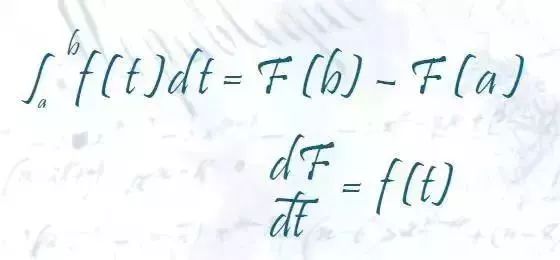
微积分是微分和积分的总称,“无限细分”就是微分,“无限求和”就是积分。比如,炮弹飞出炮膛的瞬间速度就是微分的概念,炮弹每个瞬间所飞行的路程之和就是积分的概念。
微积分的诞生是数学史上,也是人类历史上最伟大最有影响的创举,因为从此数学家和科学家在讨论连续变化的数量时便有了科学依据。化学、生物学、地理学、现代信息技术等学科运用微积分的方法推导演绎出各种新的公式、定理,促成了后来一切科学和技术领域的革命。离开微积分,人类将停止前进的步伐。恩格斯曾说:在一切理论成就中,未必再有什么像17世纪下半叶微积分的发现那样被看作人类精神的最高胜利了。

蔡志忠漫画《人生是时间的微积分》——少林寺石碑
公式背后的故事:
牛顿和莱布尼茨几乎是同时独立地发明了微积分,莱布尼茨稍晚几年。在1673到1675年之间的某个时刻,莱布尼茨曾与牛顿联系,想知道牛顿到底已经知道了些什么,并提出了某种交换信息的建议:你告诉我这个,我就告诉你那个。牛顿在回信中透露了微积分基本定理,但把它隐藏在一个难以破解的字母易位字谜中。牛顿显然并不想与莱布尼茨分享他的发现。他只是要留下伏笔,一旦莱布尼茨以后说这一定理是他自己的,牛顿就可以此证明他才是第一个发明人。敢情伟大的科学家也这么小心眼儿呢!
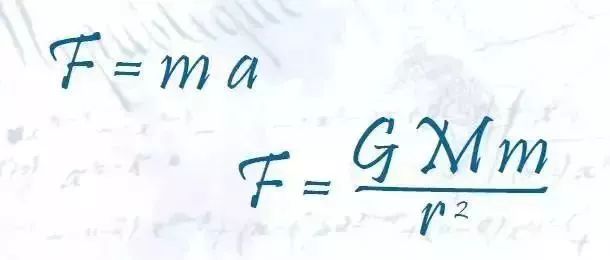
经典物理学中最伟大的没有之一的核心定律。学过高中物理的你,还记得它们吗?

公式背后的故事:1684年,牛顿的朋友埃德蒙顿·哈雷问牛顿能否证明行星的轨道是椭圆,牛顿说他能。结果三年后,牛顿对这一问题的论证便形成了《自然哲学的数学原理》,该书第一部分就开宗明义叙述了牛顿三大定律,为将来的一切物理学书籍定下了基调。
哈雷慷慨解囊,赞助牛顿出版了此书,他的这一义举最终以一种非常独特的方式得到了回报:除了对苹果和行星以外,牛顿的理论也可应用于彗星。因为彗星的轨道是椭圆,所以它们一定会一次又一次地回归。哈雷意识到,人们曾多次观察到一颗特定彗星,它以大约75年的周期回归:1456年、1531年、1606年和1682年。于是他正确地预测了这颗彗星将会在1758年(那时他早已离世)再次回归。从那时起,这颗彗星每隔75至76年就会回归一次,这就是著名的哈雷彗星。
NO.7 麦克斯韦方程组















