越想
越魔性
各位模友
请准备好你的想象力
拓扑学是一门很有魔性的学科，如果问我拓扑学对于我有什么用，我會说“一、很好玩，二、帮我理解了四維图形。
今天小编想说的，是我怎么通过拓扑学理解四维空间的。实际上作为愚蠢的人类，我还是想象不出四维空间到底是个什么样。
拓扑学是一门与几何非常相关的学科，而且，在某些问题上，拓扑学表现出超乎寻常的魔性。咱们从几个拓扑学问题入手吧。
问题1：在一个轮胎的表面上打一个洞。能否通过连续变换，把这个轮胎的内表面翻到外面来？
问题2：能否把左图连续地变形为右图？
答案是：都可以！
问题1
首先，作出如下图所示的连续变换。可以看到，一个表面有洞的轮胎本质上等于两个粘在一起的纸圈！不过，注意纸圈 1 和纸圈 2 的地位不太一样：一个是白色的面（即最初轮胎的内表面）冲外，一个是阴影面（即最初轮胎的外表面）冲外。现在，把纸圈 2 当成原来的纸圈 1 ，把纸圈 1 当成原来的纸圈 2 ，倒着把它们变回轮胎形，轮胎的内外表面也就颠倒过来了。
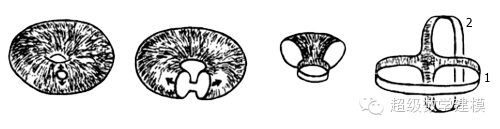
有趣的是，把轮胎的内表面翻出来之后，轮胎上的“经线”和“纬线”（姑且这么叫吧）也将会颠倒过来：
Wikipedia 上有一个巨帅无比的动画，直接展示出了把一个圆环面的内表面翻到外面来的过程。此动画看着非常上瘾，小心一看就是 10 分钟！
问题2
答案是可以的。首先，作出如下图所示的连续变换，于是就变成了问题 1 中的图 (a) 。再利用问题 1 的办法，即可变出我们想要的形状来。
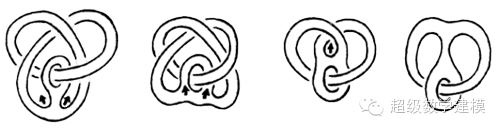
在拓扑学中，只要两个物体，他们的连着的东西数量没变，变换的时候没有割开两三块，就是拓扑等价、拓扑变换。
举个栗子
这意味着，假如人类的身体可以像橡胶人一样任意变形，那么用两手的拇指和食指做成两个套着的圆环之后，我们可以不放开手指，把圆环给解开来。 Algorithmic and Computer Methods for Three-Manifolds 一书里画了一张非常漂亮的示意图：
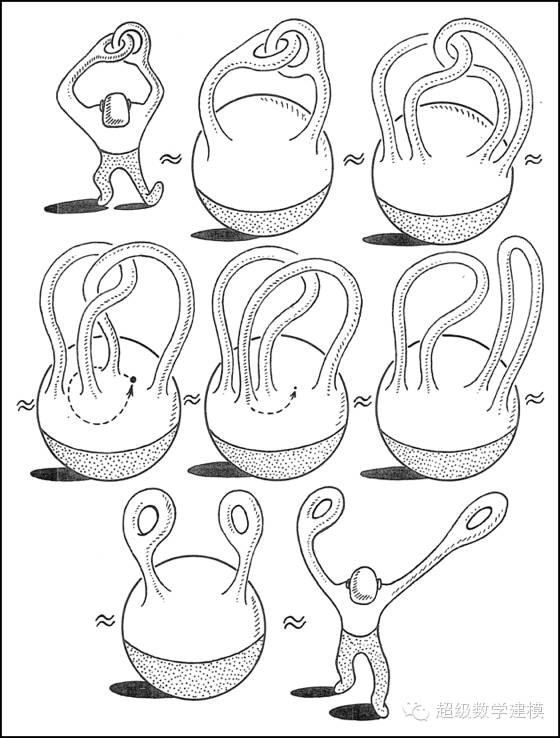
啥叫拓扑等价？ 拓扑变换？
在拓扑变换下，点、线、块的数目仍和原来的数目一样，这就是拓扑等价。一般地说，对于任意形状的闭曲面，只要不把曲面撕裂或割破，他的变换就是拓扑变幻，就存在拓扑等价。
直白的说，就是只要是连着的东西数目、穿的孔数目不变，就是拓扑等价的，正方体四面体球体统统是拓扑等价的！（有一个穿孔的正方体跟有一个穿孔的棍子也是拓扑等价的）
只要不把原来的东西割开分离，就是拓扑变换。 拿上面的人做栗子，如果把他的手腕割开一圈，就不是拓扑变换。
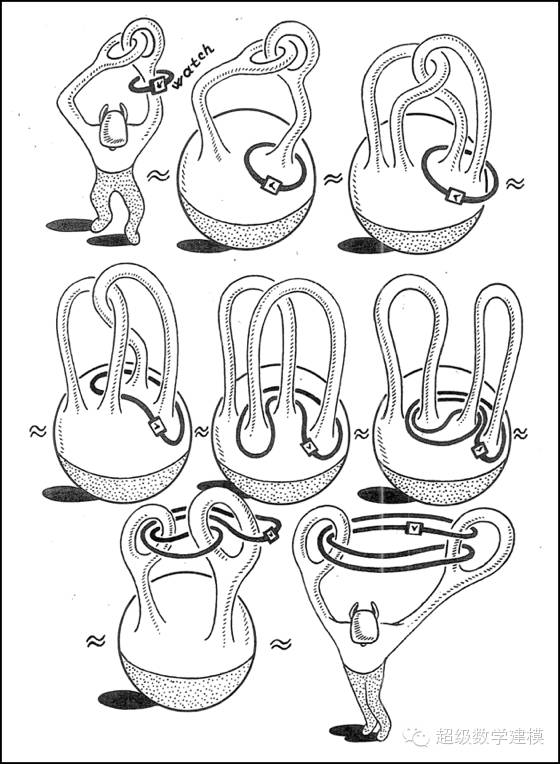
比如说下面这些东西都是拓扑等价的
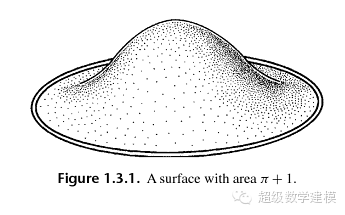
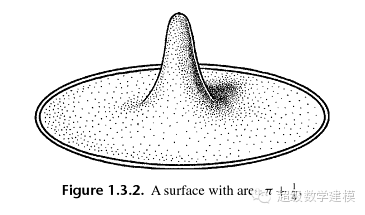
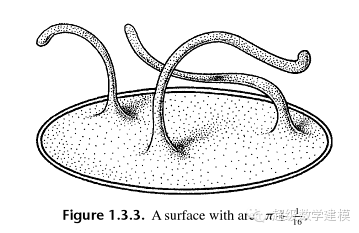
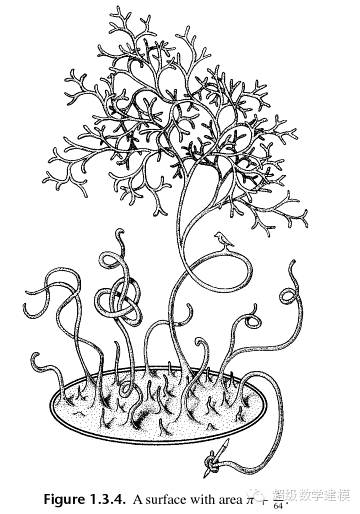
（那支铅笔不算！）
跟四维空间的一毛钱关系
关于四维空间，小编是通过这两张图顿悟的，其实主要是类比和融会贯通。现在我在兴致勃勃地研究四维空间里的拓扑性质。
这张图实际上是围成这个圈的曲面绕着包围的空间旋转一周的情景！
因为是拓扑变换，所以实际上旋转过后围着的空间没有改变！
这可以说是三位维空间的拓扑变换。
（注，上面这张图主要表现面，请关注面包住的体积，我没找到图）
这是四维正方体旋转的情形，实际上就是围成这个四维图形的正方体绕着他包围的四维空间旋转一周的情形！（我们的肉眼看到其实是投影）
这可以说是四维空间的拓扑变换。
有点感觉了吗？
小编最初对四维空间的了解来自这张图
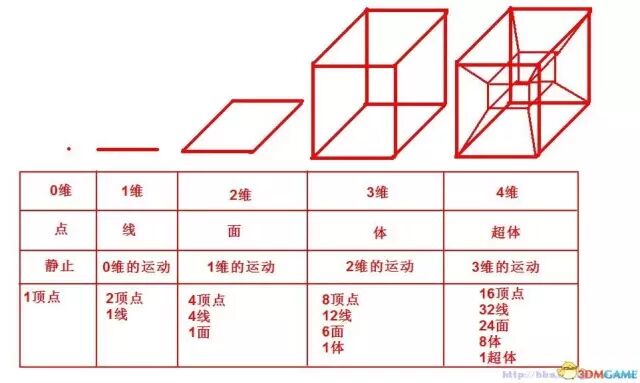
我来解释一下：其实上面这张图里的东西都不能很好解释。
从一维空间到四维空间
假如我们以点作为空间的基本元素，那么在二维空间里，至少两个点规定了一个二维空间范围，就是直线（曲线）。
至少三个直线（或曲线闭合）就规定了一个面（曲面）。
至少四个面（或曲面闭合），就规定了一个体。
那么，至少五个体（或体闭合），就成了个超体。
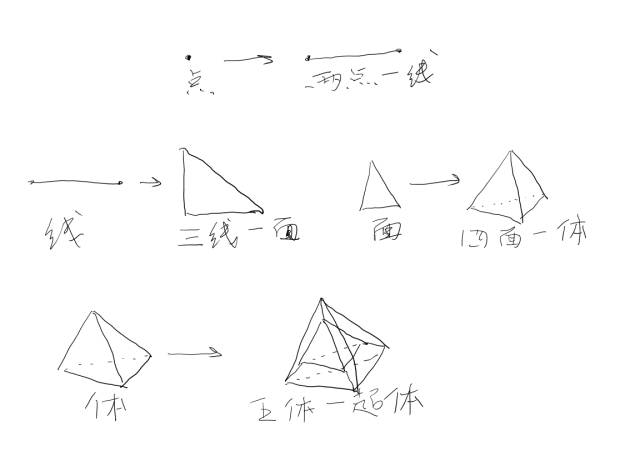
在机器学习中，有个概念叫超平面，可以从这里理解下，小编理解那个理解了很久
干货：机器学习算法基础知识
都是投影
实际上，在平面上看到的三维图形和四维图形都是二维投影（比如此时您在手机上看的都是投影）
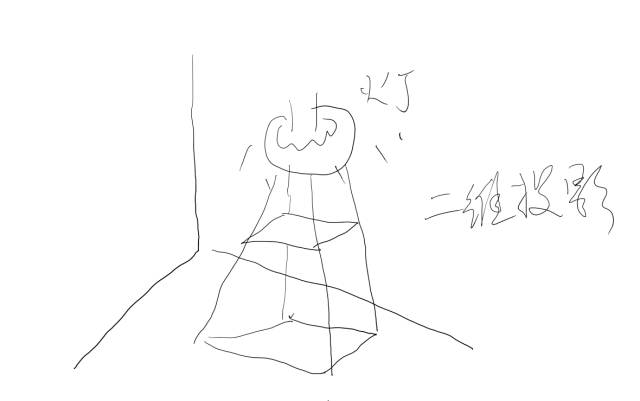
二维图形映射在二维图形上能保留原来的形态（拓扑等价，不过大小可能变了）
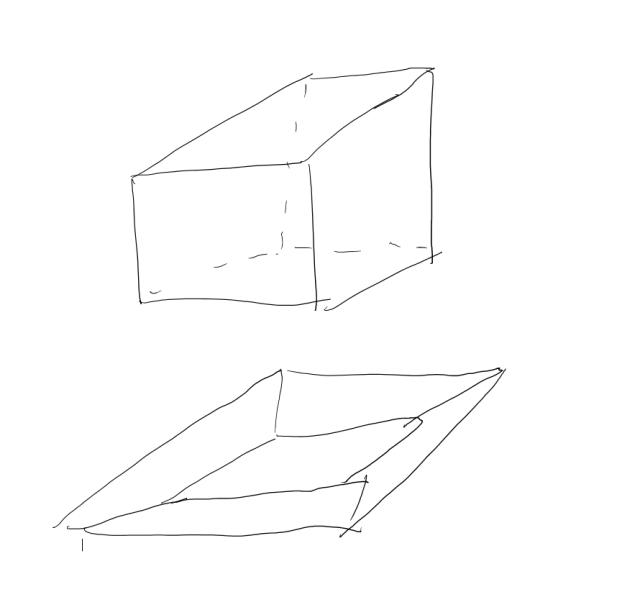
三位图形映射到二维平面上就只能通过透视效果感受了，你看到的是一个映像。
四维图形映射到三位空间只能是这样了（抱歉，我们没有全息投影服务，这个图形也是通过二维表现三维，不过您还是能想象出来的）
我曾经盯着这张图发了整节课呆
关于拓扑和空间
小编又想起这张图了。。。。
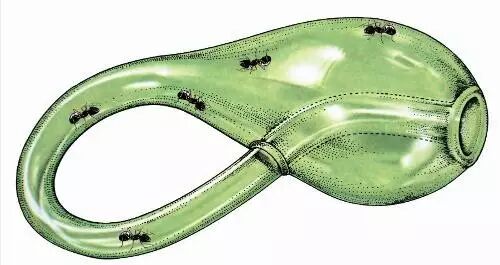
你可以把这个看作莫比乌斯环的三维推广。
我决定了，我一定要跪着走完莫比乌斯环。
本文由超级数学建模编辑整理
资料来源于网络
转载请在公众号中，回复“转载”
-----这里是数学思维的聚集地------
“超级数学建模”（微信号supermodeling），每天学一点小知识，轻松了解各种思维，做个好玩的理性派。20万数学精英都在关注！
超模大学堂的第一节数模课程
让你明白数学建模到底有什么用
▼点击「阅读原文」，可报名此课程
