
►
概率论还能识别“财务造假”?
上文介绍了
几个概率中的悖论
,其中提到了一个与几何概型有关的贝特朗悖论。概率论中的悖论很多,基于经验的直觉判断很多时候往往并不靠谱。今天这篇将介绍的本福特定律,也是一条初看起来有些奇怪、不合直觉的定律,不过这条定律用处却很大,甚至还能帮助侦破“财务造假”。
撰文 | 张天蓉
责编 | 吕浩然
●
●
●
2017-03-16
上帝教人掷骰子——“神童”帕斯卡与概率论
2017-03-31
似是而非的答案:概率论悖论
弗兰克·本福特
(Frank Benford, 1883–1948)
本是一个美国电气工程师,却在中年时迷上了一个与概率有关的课题,课题得到的结论便是现在我们所说的“本福特定律”。该定律大致意思是说,在众多真实数据中,以“1”为首位数字的数出现的概率约占总数的三成,接近期望值1/9的3倍。
我们举一个例子说明它。
设想某银行有1000多个储蓄账户,存款金额不等。奇怪的是,本福特定律对这些存款金额本身并不感兴趣,而对这些数值的开头第一位有效数字
(非零)
颇为中意。我们都知道,一个数的第一位
(非零)
有效数字可能是1到9之间的任何一个。现在,如果我问,在刚才那个银行的上千个存款数据中,第一位数字是1的概率是多大?
无需多思,大部分人都会很快地回答:应该是1/9吧。因为从1到9,9个数字排在第一位的概率是相等的,每一个数字出现的概率都是1/9,大约11%左右。

►
图1:本福特定律(首位数定律)
从这种听起来十分正常的思维方法得出的结论却与许多真实数据所遵循的规律不同。人们发现,很多情况下,第一个数字是1的概率要比靠直觉预料的11%大得多。数字越大,出现在第一位的概率就越小,数字9出现于第一位的概率只有4.5%左右。各个数字出现在第一位的概率遵循如图1左图所示的概率分布。从图中可以看出,首位数字为1的概率可达30.1030%,而首位数字为9的概率仅为4.5757%。
事实上,本福特定律的发现者另有其人:美国天文学家西蒙·纽康
(Simon Newcomb,1835 - 1909)
。纽康在查阅对数表(常用对数编排而成的表格,用以计算)时发现了一个奇怪的现象:包含以1开头的数的那几页比其他页破烂得多,似乎表明计算所用的数值中,首位数是1的概率更高,因此他在1881年发表了一篇文章提到并分析了这个现象
【3】
,但没有引起人们的注意,直到57年之后的1938年,本福特又重新发现这个现象。
说来令人奇怪,科学定律的发现有时候来自于一些毫不起眼、小得不能再小的现象,本福特的发现便是如此。“以1开头的数字比较多”,这也算是一个定律吗?本福特发现这种现象不仅仅存在于对数表中,也存在于其它多种数据中,于是,本福特检查了大量数据而证实了这点。
【4】
本福特和纽康都从数据中总结出首位数字为n的概率公式是:

其中d取决于数据使用的进位制,对十进制数据而言,d=10。
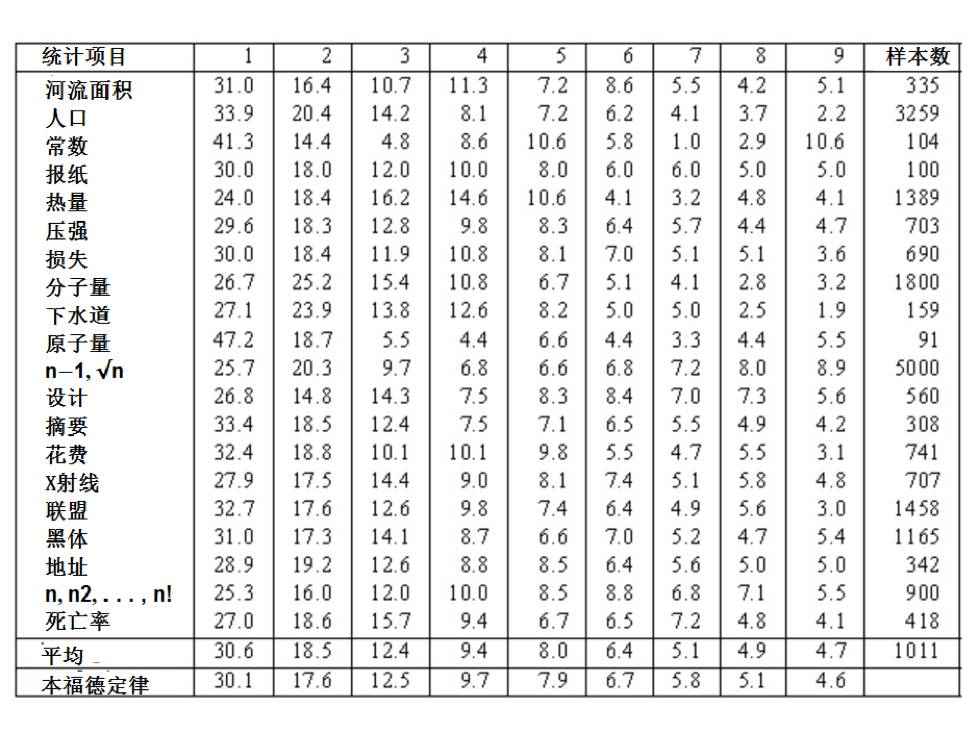
随后,本福特收集并研究了20229个统计数据,包括河流面积、人口统计、分子及原子重量、物理常数等多种来源的资料,并分成20组。数据来源虽然千差万别,却基本上符合本福特定律,见图2所示的数据表。表中最后一行的数值,是根据本福特概率公式计算得到的每个数字出现于首位的概率,读者可以将它与真实数据相比较。
►
图2:本福特从大量数据中得到的首位数字概率表
本福特定律适用范围异常广泛,自然界和日常生活中获得的大多数数据都符合这个规律。尽管如此,此规律仍然受限于如下几个因素:1. 这些数据必须跨度足够大,样本数量足够多,数值大小相差几个数量级;2. 人为规则的数据不满足本福特定律,例如按照某种人为规则设计选定的电话号码、身份证号码、发票编号等等。为造假而人工修改过的实验数据、彩票上的随机数据也不符合本福特定律。
尽管本福特和纽康都总结出了首位数字的对数规律,但并未给出证明,直到1995年美国学者Ted Hill才从理论上对该定律作出了解释,并进行了严谨的数学证明
【5】
。虽然本福特定律在许多方面都得到了验证和应用,但对于这种数字奇异现象人们依旧是迷惑不解。到底应该如何直观理解本福特定律?为什么大多数数据的首位数字不是均匀分布而是对数分布的?
有人探求数“数”的方法,来直观解释本福特定律。他们的意思是说,当你计算数字时,顺序总是从1开始的,如果到9就终结的话,所有数字起首的机会都相同,但9之后的两位数10至19,以1起首的数则远多于其它数字。
我们可以用这种方法来理解街道号码
(地址)
一类的数据。一般来说,每条街道的号码都是从1算起,街道长度有限,号码排到某一个数就终止了。另一条街又有它自己的从1开始的号码排列,以此类推,1开头的号码是要多一些的。但这种解释也太不“数学”了!况且,这种理解无法说明另外一类数据为什么也符合本福特原则,如“物理常数”的集合、出生率、死亡率等,这些数据并不是从1开始计算到有限长度就截止的那种数据。
另一种解释是认为本福特定律的根源是由于数据的指数增长。指数增长的序列,数值小的时候增长较慢,由最初的数字1增长到另一个数字2,需要更多时间,所以出现率就更高了。
举个例子来说明这个道理:如果你有100美元的存款,年利率是10%,25年中,你每年的存款金额将是
(只保留了整数部分)
:
100、110、121、133、146、161、177、195、214、236、259、285、314、345、380、418、459、505、556、612、673、740、814、895、985
这是一个指数增长的序列。在这组数据的25个数字中,首位数字为1的有8个
(32%)
;2的4个;3的3个……9的只有1个
(4%)
。这是因为从首位为1增加到首位为2,经过了更长的时间
(8年)
;从首位为2,只经过了4年就变成了首位为3;而首位为9的话,下一年又变成了1。所以,指数增长规律的数列的确符合本福特定律。
读者也许会有疑问:上面的数列选择从100开始,1打头的比较多,如果从别的数字开始,规律是否会改变呢?读者可以试验一下,得到的结果仍符合本福特法则。此外,你还可以将美元换算成人民币
(乘以6.7)
,得到的数据仍然会遵循本福特定律,这也说明本福特定律具有“尺度不变性”。
由于大多数财务方面的数据都满足本福特定律,因此,在现实生活中,它可以用作检查财务数据是否造假!
美国华盛顿州曾侦破过一个当时最大的投资诈骗案,金额高达1亿美元。诈骗主谋凯文·劳伦斯及其同伙以创办高技术含量的连锁健身俱乐部为名,向5000多个投资者筹集了大量资金。随后,他们挪用公款以作自身享乐。为了掩饰他们的不法行为,他们将资金在海外公司和银行间进行频繁转账,并且人为做假账,制造一种生意兴隆的错觉。
所幸,当时有一位名为Darrell Dorrell的会计师感觉不对头,他将70000多个与支票和汇款有关的数据收集起来,将这些数据首位数字发生的概率与本福特定律相比较,发现这些数据无法通过本福特定律的检验。最后经过了3年的司法调查,终于拆穿了这个投资骗局
【7,8】
,2002年,劳伦斯被判20年牢狱。
2001年,美国最大的能源交易商安然公司
(Enron Corporation)
宣布破产,并传出公司高层管理人员涉嫌做假账的传闻。据传,安然高层改动过财务数据,因而他们所公布的2001-2002年每股盈利数据不符合本福特定律
【6】
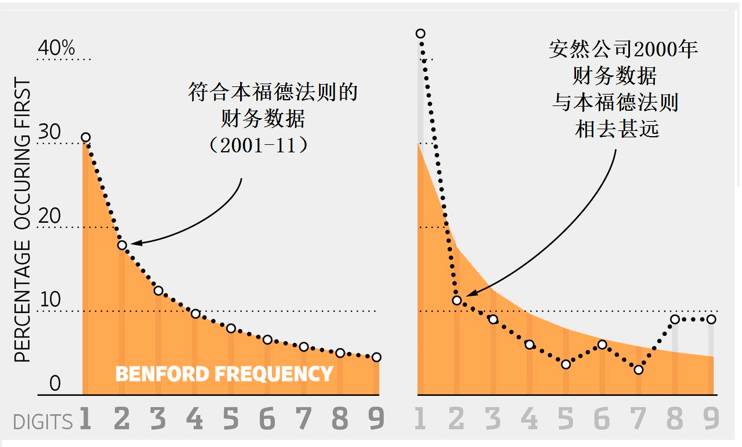
。此外,本福特定律也被用于股票市场分析、检验选举投票欺诈行为等。
►
图3:安然公司数据vs本福特定律(图片来源:
The wall street journal
【6】
)
概率论由研究赌博问题而诞生,又在不断地提出及解决各种有趣的赌博问题中发展起来。且听我们在下一篇中,介绍大数定律以及更多与赌博有关的概率问题。
趣味拾遗:
“三门问题”
除了前文提到的贝特朗悖论,他在1889年还提出了另一个“悖论”——贝特朗盒子悖论,之所以加上引号是因为实际上它并不算是一个真正的悖论,因为在逻辑上它并不矛盾。但它却是一个与博弈论相关的、非常有趣的数学游戏。
“三门问题”有好几个等效版本,最早的一版可追溯到19世纪的贝特朗,该问题在数学本质上也等同于马丁·加德纳(Martin Gardner,1914 - 2010)1959年提出的“三囚犯问题”
【1】
。不过,这些老版本默默无闻,直到上世纪九十年代,美国著名的电视游戏节目Let's Make a Deal才让其火了一把。由此也足可见现代媒体在公众中普及科学知识的重要性。
当年的节目主持人蒙特·霍尔(Monty Hall)善于与参赛者打心理战,经常突如其来地变换游戏规则,既使得观众们困惑不已,又迫使参赛者“脑筋急转弯”。三门问题及各种变通版本便是他经常使用的法宝。后来有人便将此游戏以主持人的名字命名,也称之为蒙特·霍尔问题
【2】
。
三门问题大致是说在三扇门的后面,分别藏着汽车和两只山羊。如果参赛者选中了后面有汽车的那扇门,便能赢得该汽车作为奖品。显而易见,在这种情况下参赛者赢得汽车的概率是1/3。
►
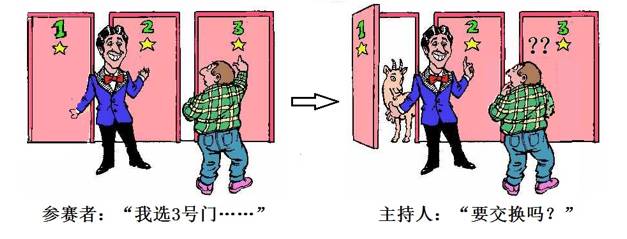
三门问题
不过,蒙特·霍尔在一次节目中却改变了一点规则:当参赛者选择了一扇门但尚未打开之际,知道门后情形的他说:
“等等,我现在给你第二次机会。首先,我将打开你没有选择的两扇门中有山羊的一扇,你可以看到门内的山羊。然后,你有两种选择:改变你原来的选择(交换),或者保留原来的选择(不交换)。”
要不要交换?我们不从“碰运气”而是从“概率”的角度来思考这个问题。如果不交换,保持原状的话,得汽车的概率是1/3;如果交换的话,是否能增加抽到汽车的概率呢?答案是肯定的:改变选择(交换)可以将参赛者赢得汽车的概率从1/3增加到2/3。
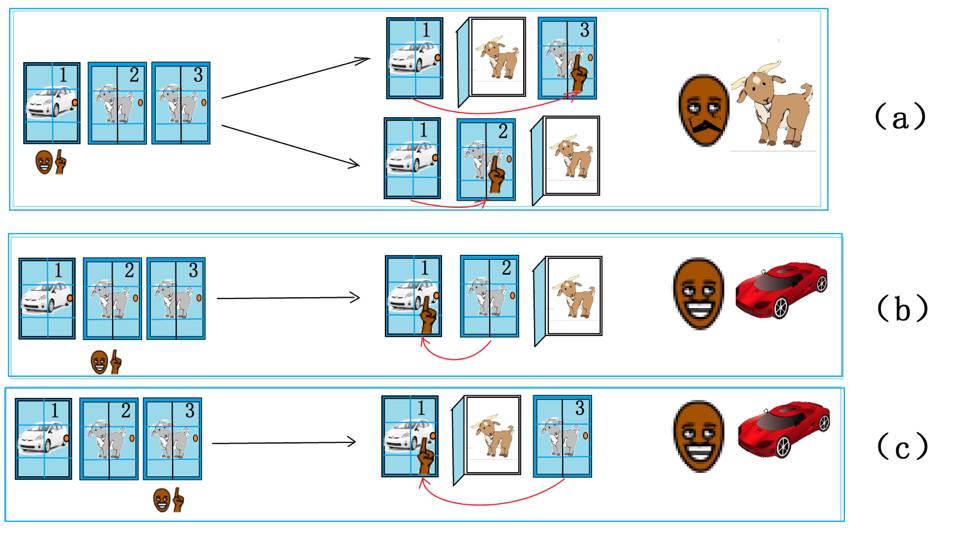
让我们来分析一下整个游戏过程:参赛者指定3道门中的一道,在选择交换之后可能遇到图2显示的三种等概率(1/3)情况。
(a)参赛者挑选有汽车的第1道门,主持人挑两头羊的任何一头交换都将失败。
(b)参赛者挑选有羊的第2道门,主持人打开第3道门,交换将赢得汽车。
(c)参赛者挑选有羊的第3道门,主持人打开第2道门,交换将赢得汽车。
►
改变选择使得参赛者获得汽车的概率变为2/3
我们也可以换一种思维方式来理解这个问题。参赛者最初选到汽车的概率是1/3,选到羊的概率是2/3。如果参赛者先选中汽车,那么交换之后一定“输”;如果先选中羊,换后则一定“赢”。因此,选择“交换”而获得汽车的概率,就是开始是选到羊的概率,为2/3。
也许三门问题的解释仍然有些使人困惑之处,但如果将门的数目增加到10道门(主持人开启8道有“羊”的门,留下1道),参赛者选择“交换”使概率增加的结论便显而易见了。

►
十门问题
参考资料:
【1】Gardner, Martin (1959). "Mathematical Games" column, Scientific American, October 1959, pp. 180–182.
【2】Bohl, Alan H.; Liberatore, Matthew J.; and Nydick, Robert L. (1995). "A Tale of Two Goats ... and a Car, or The Importance of Assumptions in Problem Solutions". Journal of Recreational Mathematics 1995, pp. 1–9.
【3】Newcomb, S (1881). "Note on the frequency of use of the different digits in natural numbers". American Journal of Mathematics. 4 (1): 39–40.
【4】Benford, F. (1938), The law of anomalous numbers, Proc. Amer.
Philosophical Soc. 78, 551–572.
【5】Hill, T. P. "A Statistical Derivation of the Significant-Digit Law." Stat. Sci. 10, 354-363, 1996.。
【6】“The wall street journal”
https://www.wsj.com/articles/accountants-increasingly-use-data-analysis-to-catch-fraud-1417804886
【7】Judge Sentences Kevin L. Lawrence to 20 Years Prison in Znetix/HMC Stock Scam
http://www.dfi.wa.gov/news/press/judge-sentences-kevin-l-lawrence-20-years-prison-znetixhmc-stock-scam
【8】The Drunkard's Walk: How Randomness Rules Our Lives
By Leonard Mlodinow,pp. 84, Published by Pantheon Books
(Audio book from amazon.com:
https://www.amazon.com/Drunkards-Walk-Randomness-Rules-Lives/dp/B001BSJHRC)
制版编辑:邓志英
丨
本页刊发内容未经书面许可禁止转载及使用
公众号、报刊等转载请联系授权
[email protected]
▼点击查看相关文章
精子治癌
|
特殊使命
|
钱与竞争
|
造假
|
奥数
最欢迎
|
西湖
|
农场
|
学术辩
|
日本奖
|
遗作
屠呦呦
|
王晓东
|
白岩松
|
何江
|
张锋
|
霾
杨振宁
|
卢煜明
|
王小凡
|
女性成就
|
张纯如
 ▼
▼
▼
点击“阅读原文”,牵手科学队长!
▼
▼
▼
点击“阅读原文”,牵手科学队长!





