
来源 | Medium
译者 | 磐石001
虽然,深度学习在近几年发展迅速。
但是,关于如何才能设计出最优的卷积神经网络架构这个问题仍在处于探索阶段。
其中一大部分原因是因为当前那些取得成功的神经网络的架构设计原理仍然是一个黑盒。
虽然我们有着关于改进神经网络表现的丰富心得,但其实并没有真正了解神经网络是如何达到当前这么优秀的表现。
关于CNNs的一些线索
我们从如下几点开始剖析。
近期研究提供了一些具体地证据证明这几点确实可以用来提升CNN的表现:
-
增加图像分辨率
-
增加网络深度
-
增加网络宽度
-
增加跳过连接(密集块或残差块)
经验表明,以上几种方式是使得CNN之所以取得最优结果的关键。
增加图像的分辨率可以“喂养”网络更多的信息去学习;
增加网络宽度与深度使网络学习到更多的参数。
另外,增加“跳过连接”可以增加网络的复杂性,从而增强网络的表征能力。
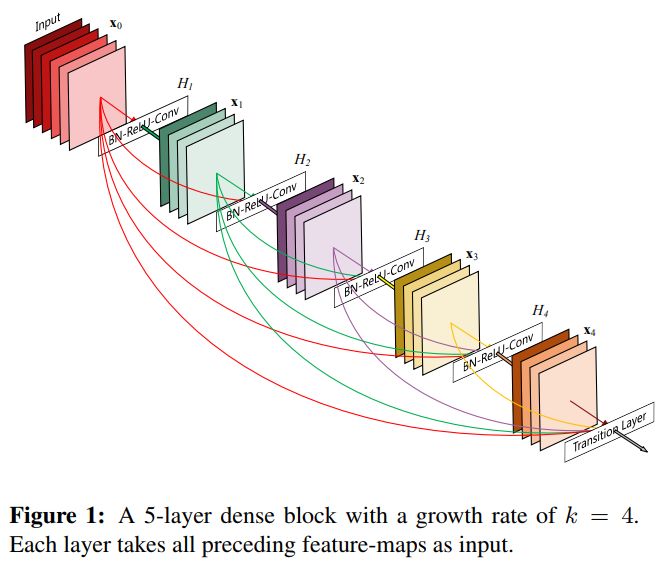
密集连接块(DenseNet)
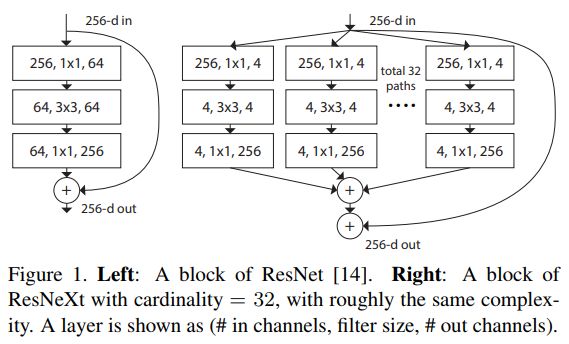
一个宽网络上的跳过连接(ResNext)
神经架构搜索
NAS是一种寻找最优神经网络架构的算法。
绝大多数NAS算法工作原理类似。
首先,定义一组适用于我们网络的“构建块”。
然后,尝试以不同的方式组合这些“构建快”进行训练。
通过这种试错方式,NAS算法最终能够确定哪一种“构建快”与哪一种网络配置可以得到最优结果。
事实证明,这种方法行得通且可以找到最优的预测效果。
如NASNet的论文中所示,可以组合出一些奇怪的结构。
如下:
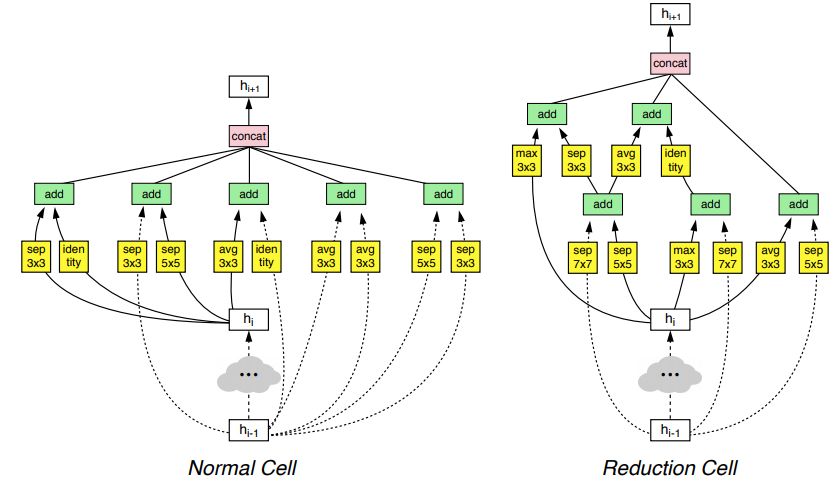
通过NAS算法发现的NASNEt块
这也正是NAS的伟大之处之一,可以让我们发现一些之前还未探索过的网络结构。
然而,它也有自己的局限性。
由于其从一组固定的“构建快”开始采样和进行组合,所以我们将不能通过此算法发现新的构建块。
跳过连接也是如此,NASNet只允许含有一次下采样的跳过连接,但其他类型的连接也同样值得尝试。
Facebook的人工智能研究团队通过“随机连接神经网络(randomly wired neural networks)”对NAS进行新的尝试。
它们的动机是:
如果“架构搜索”在固定的块和连接上表现得很好,那么在更大的搜索空间下(例如:
随机连接)将会产生一些更优的配置。
随机连接神经网络
由于论文作者想要专门研究神经网络的连接方式,所以他们对网络结构做了如下限制:
-
网络输入尺寸为224x224
-
网络块始终为ReLU-Conv-BatchNorm三项组形式。且三项组中的卷积都是参考自Xception结构中使用的3x3可分离卷积。
-
多组张量的聚合(例如当跳过连接与原连接进行聚合时)均以加权和的方式进行聚合。这些权重具有可学习性与可持续更新性。
-
网络组成总是保持一致。
一般的CNN结构是由多个卷积块组成,然后通过多次向下采样,直到最终的softmax分类层。
这也已经成为网络设计的标准。
在这些研究实验中均采用了这种范式。
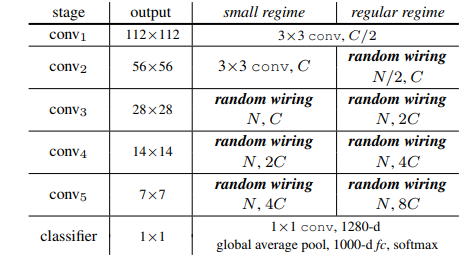
通用CNN结构范式
ImageNet竞赛的标准输入尺寸为224x224--ImageNet数据集被用来作为一个基线数据集来检验“手工网络”(NAS算法生成的网络架构)的性能。
ReLU-Conv-BatchNorm三项组块也很常见,而且已经被广泛证明成为了可以为深度卷积神经网络带来最优的效果。
张量聚合的方式不止一种,很多优异的网络在没有进行加权的情况下直接进行求和或连结--但不会对性能造成较大的影响。
上述表格中描述的这些过去常用的网络结构同样也用在了ResNets,DenseNets和NASNets中。
注意,这并不是一个完全的随机神经网络。
它并不是完全从零开始随机化。
而是在其他组件保持不变的情况下,针对CNN设计过程中一个被称为“连接(wiring)”的单一组件进行探索。
作者试图让读者明白的一个重要观点--他们还没有实现完全意义的随机化神经网络,但正开始对组件搜索空间一步一步的进行深入的探索。
在这些约束条件下,各种经典的随机模型图被用来生成网络的随机连接。
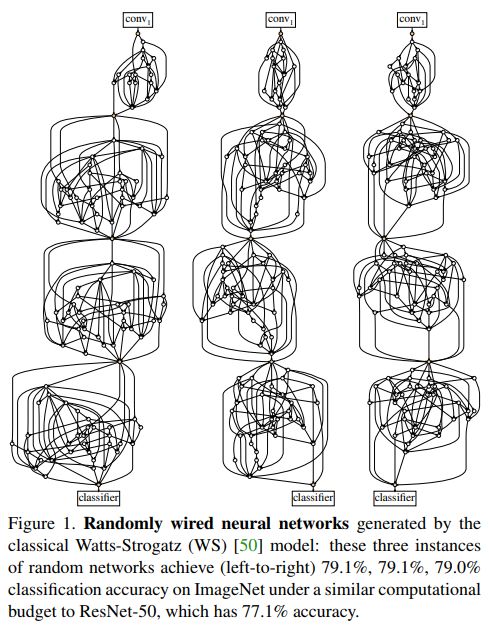
一些随机连接网络结构
随机网络打开了深度学习探索的大门
本研究的意义在于其探索性思想:拓展NAS算法的搜索空间,寻找新的、更好的网络设计。
虽然研究人员已经发现了一些很棒的设计,但是以手动尝试的方式遍历整个搜索空间实际上是不可行的。
这也扩展到了另一观点:如果我们要扩展搜索空间,我们需要一种擅长搜索的算法(在本例中用的是网络生成器),。
这种算法必须知道要寻找什么,或者至少类似梯度下降优化算法有着通过设计向优化方向靠拢的趋势。
架构搜索是深度学习研究的下一个前沿领域。
它使我们可以使用算法来发现最优的网络架构,而不是反复进行试验。
目前,在搜索其他组件(在本例中是“连接方式”)时修复一些网络组件已经成为可能。
这将问题简化为更容易处理的小问题。
由于这是我们发现新颖架构的唯一方法,NAS算法应该具备一定程度的随机性。
下一步是进一步扩展搜索空间和增情搜索算法的随机性。
这意味着随机搜索思想将扩展到网络中越来越多的组件上,直到全部网络组件均可以被算法自动设计好为止。
当实现完全意义的NAS时会发生什么?它会选择像2x4这样的非平方卷积吗?它会使用反馈循环吗?网络变得更简单还是更复杂?
神经架构搜索是一个令人兴奋的新兴研究领域。
希望搜索算法变得更加具有随机性从而实现利用随机化的方式发现创造性的、以前从未想到过的架构。















