现代雷达系统_第三次作业_王怀帅_202018019427053

正文

1、证明：由理想点源天线构成的一维线性均匀阵列天线(如图所示)，扫描角度为 $\theta$ ，为保证天线方向图不出现栅瓣，阵元之间的距离 $D$ 必须小于 $\frac{\lambda }{1+|\sin \theta |}$ 。

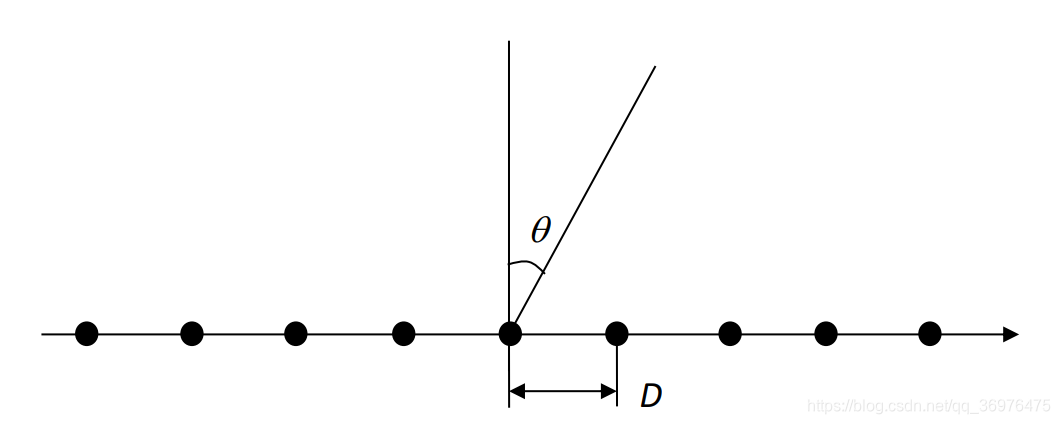
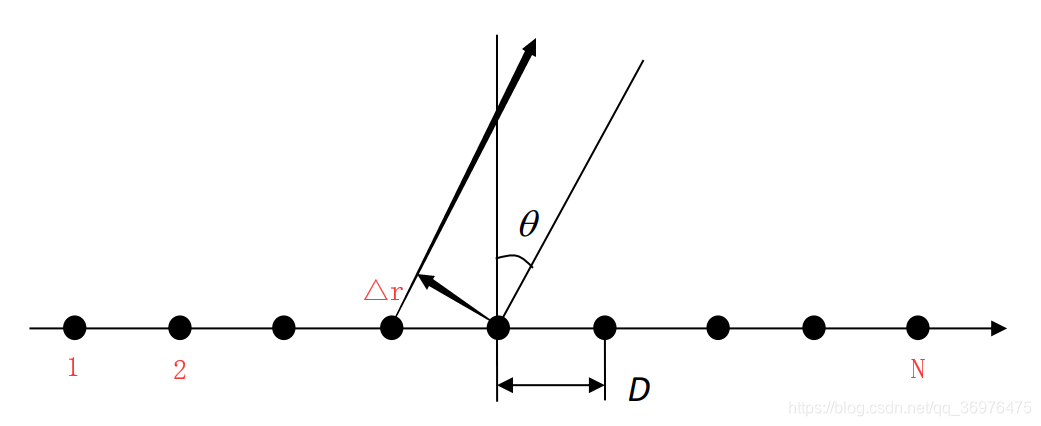
设相邻阵元的总相位差为： $u=k▽r+\psi =kd\sin \theta +\psi$ ， $\psi$ 为相邻单元的馈电相位差

则阵列天线的总辐射电场为：

$$\begin{array}{rl}E(\theta )& =\sum _{n=1}^N{e}^{j(n-1)(kd\sin \theta +\psi )}\\ & =1+e^{j(kd\sin \theta +\psi )}+\cdots +e^{j(N-1)(kd\sin \theta +\psi )}\\ & =\frac{1-e^{jN(kd\sin \theta +\psi )}}{1-e^{j(kd\sin \theta +\psi )}}\\ & =\frac{1-\cos (N(kd\sin \theta +\psi ))-j\sin (N(kd\sin \theta +\psi ))}{1-\cos (kd\sin \theta +\psi )-j\sin (kd\sin \theta +\psi )}\\ |E(\theta )|& =\sqrt{\frac{[1-\cos (N(kd\sin \theta +\psi )){]}^2+[\sin (N(kd\sin \theta +\psi )){]}^2}{[1-\cos (kd\sin \theta +\psi ){]}^2+[\sin (kd\sin \theta +\psi ){]}^2}}\\ & =\sqrt{\frac{1-\cos (N(kd\sin \theta +\psi ))}{1-\cos (kd\sin \theta +\psi )}}\\ & =|\frac{\sin (N(kd\sin \theta +\psi )/2)}{\sin ((kd\sin \theta +\psi )/2)}|\end{array}$$

则归一化的方向函数为：

$$F(\theta )=\frac{|E(\theta )|}{|E(\theta {)}_M|}=|\frac{1}{N}\frac{\sin (N(kd\sin \theta +\psi )/2)}{\sin ((kd\sin \theta +\psi )/2)}|$$

当 $\psi =0$ ，即当各阵元等幅同相馈电时，由归一化的方向函数可知：

$\theta =0$ ， $F(\theta )=1$ ，即方向图最大方向在阵列法向方向上。

当 $\psi \ne 0$ 时，则方向图最大值方向就要进行偏移，偏移角 ${\theta }_0$ 由移相器的相移量 $\psi$ 决定：

改变 $\psi$ ，就可以改变波束指向角 ${\theta }_0$ ，从而形成波束扫描。

$$\psi =kd\sin {\theta }_0$$

$$(kd\sin \theta +\psi )/2<\pi$$

$$kd(\sin \theta +\sin {\theta }_0)<2\pi$$

$$\frac{2\pi }{\lambda }d(\sin \theta +\sin {\theta }_0)<2\pi$$

$$d<\frac{\lambda }{1+|\sin {\theta }_0|}$$

证毕。