
标准误是数据统计的重点概念,且难以理解。百度上文章缺乏详细描述的文章。所以写下此文让读者能够彻彻底底了解标准误概念。
标准误全称:样本均值的标准误(Standard Error for the Sample Mean),顾名思义,标准误是用于衡量样本均值和总体均值的差距。
标准误用于预测样本数据准确性 ,标准误越小,样本均值和总体均值差距越小,样本数据越能代表总体数据。
对一个总体多次抽样,每次样本大小都为n,那么每个样本都有自己的平均值,这些平均值的标准差叫做标准误。
标准差是单次抽样得到的,用单次抽样得到的标准差可以估计多次抽样才能得到的标准误差
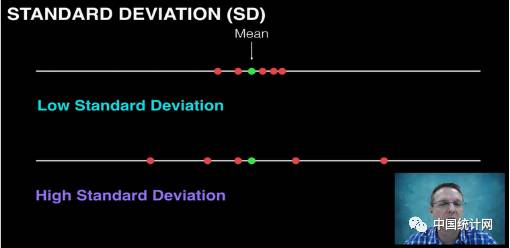
标准差表示数据离散程度:
标准差越大,分布越广,集中程度越差,均
值代表性越差
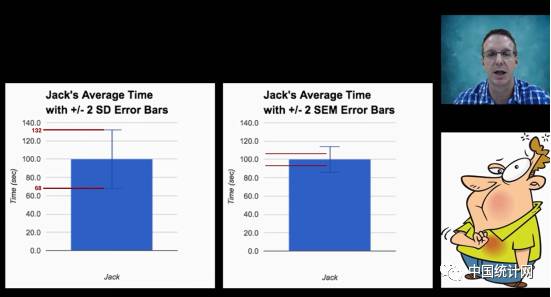
标准差与标准误不同应用范围:
标准差:(图左)在正负两个标准差(95%概
率下),Jack消耗时间在68-132秒之间。
标准误(图右)在正负两个标准误,Jack消
耗平均时间大约在95-105秒之间。
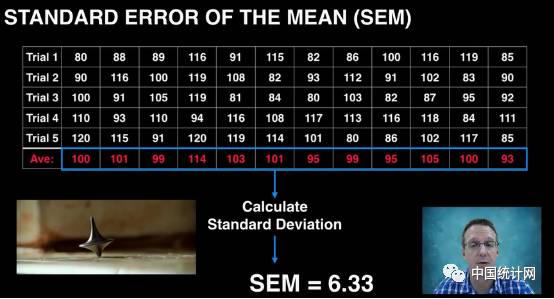
什么是真实的标准误?举个例子,对一个总体12次抽样,生成12个样本,每个样本大小都为5。那么每个样本都有自己的平均值,这些平均值的标准差叫做标准误差。这里就是对表格最后一行数组计算标准差(100,101,99,114,103.....93),最后算出来标准误结果为6.33。
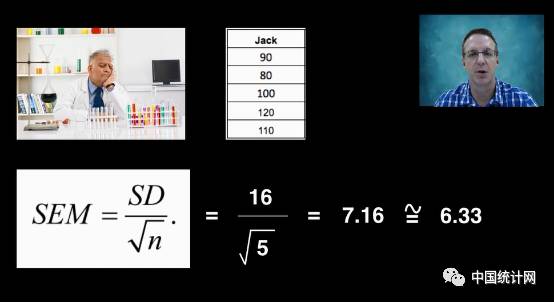
但是为了得到标准误,我们不可能做很多次科学实验。实际上我们可以做一次样本实验,然后采用估算公式:

如下图,我们用第一组样本估算真实标准误,此样本标准差除以根号n,结果为7.16, 然后把7.16约等为真实的标准误6.33。
所以标准误也是另外一种形式的标准差,标准误和总体标准差既有相似处,又有区别。标准误是一个比较难得概念,读者一次不能很好理解,如果反复看此文章,然后自己动手程序模拟,就会增强直观印象,加深理解。
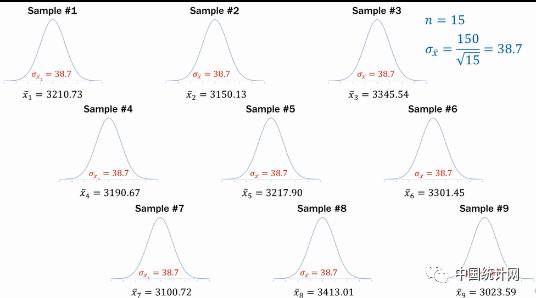
所有的随机样本中,如果数量相同,它们的标准误默认为近似相同(非真正相同)
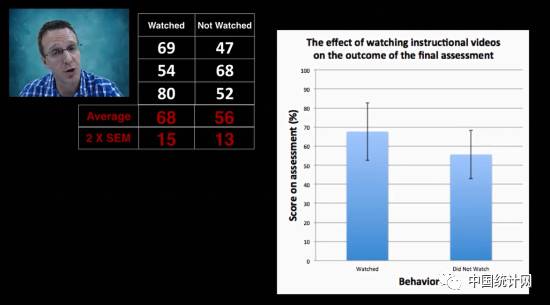
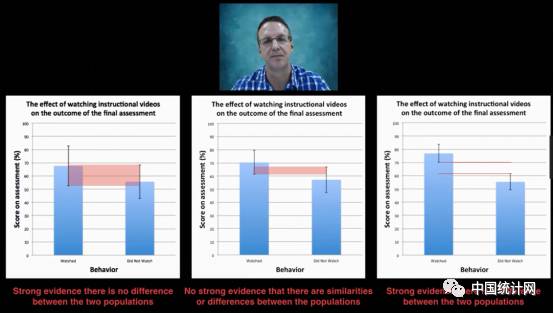
我们有两组数据,一组观看了指导视频,一组没有观看指导视频,比较两组数据在得分方面有无显著差异?
随着样本量不同,我们得到的结果不同。图左,两组数据没有区别,图中两组数据可能有区别,可能没有;图右两组数据有区别
样本量为3时,看视频组的2*标准误为15,没看视频的2*标准误为13。
样本量小时,标准误很大,样本均值和总体均值差异很大,样本数据的代表性很差。
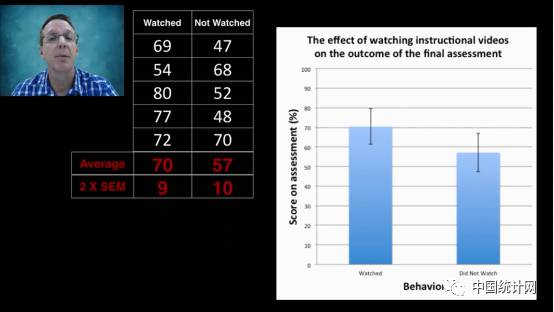
样本量为5时,看视频组的2*标准误为9,没看视频的2*标准误为10。
样本量增大后,标准误变小。
样本量为10时,看视频组的2*标准误为7,没看视频的2*标准误为6。
样本量增大后,标准误再次变小
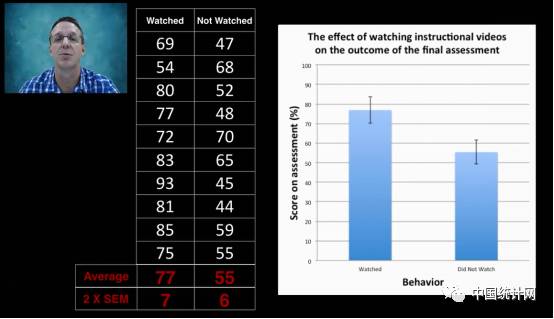
随着样本量不同,我们得到的结果不同。下面的图左(样本量为3),两组数据没有区别,图中(样本量为5)两组数据可能有区别,可能没有;图右(样本量为10)两组数据有区别。
实际上,众多毕业论文和专业期刊的统计分析都是错的,虽有华丽的可视化图表,但新手很容易因样本量太小得到错误结果。
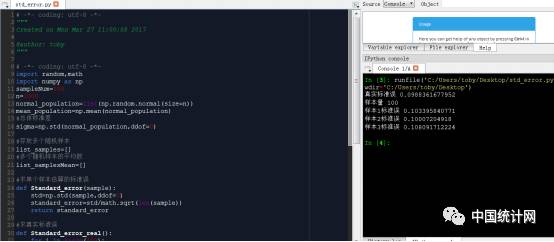
蒙特卡洛验证,对一组样本进行标准误评估,看公式SE = s/√(n)是否准确
结果表明SE = s/√(n)公式得到的标准误和真实标准误非常接近
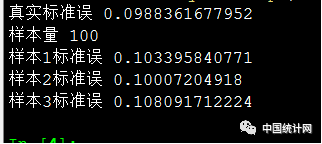
样本值100,标准误很小,大约0.1
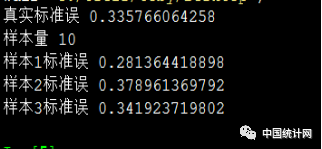
样本值10,标准误增大,大约0.33
样本值5,标准误再次增大,大约0.45
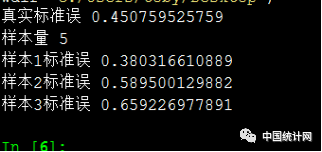
源代码如下:
问题反馈邮箱[email protected]
# -*- coding: utf-8 -*-
import random,math
import numpy as np
n=1000
normal_population=list(np.random.normal(size=n))
mean_population=np.mean(normal_population)
#总体标准差
sigma=np.std(normal_population,ddof=0)
#存放多个随机样本
list_samples=[]
#多个随机样本的平均数
list_samplesMean=[]
#求单个样本估算的标准误
def Standard_error(sample):
std=np.std(sample,ddof=0)
standard_error=std/math.sqrt(len(sample))
return standard_error
#求真实标准误
def Standard_error_real():
for i in range(100):
sample=random.sample(normal_population,100)
list_samples.append(sample)
list_samplesMean=[np.mean(i) for i in list_samples]
standard_error_real=np.std(list_samplesMean,ddof=0)
return standard_error_real
#plt.hist(normal_values)
#真实标准误
standard_error_real=Standard_error_real()
print(standard_error_real)
#随机抽样
print(Standard_error(list_samples[0]))
print(Standard_error(list_samples[1]))
print(Standard_error(list_samples[2]))
End.
作者:Toby(中国统计网特邀认证作者)
本文为中国统计网原创文章,需要转载请联系中国统计网(小编微信:itongjilove),转载时请注明作者及出处,并保留本文链接。





