专栏名称: 气象学家

【气象学家】公众号平台为您解读最新气象科研进展、分享气象实用编程技巧、追踪气象即时资讯。欢迎加入气象AI和Python交流群以及气象博士群！与5W+的专业人士一起交流互动！

Sci. Total Environ | 中国热浪和老年人口暴露的时空变化

气象学家 · 公众号 · · 2024-05-22 14:35

正文

第一时间获取气象科研资讯

『气象学家』公众号交流群

加入

编辑：不止GIS

文章简介

论文名称： Spatiotemporal variation in heatwaves and elderly population exposure across China（中国热浪和老年人口暴露的时空变化）

第一作者及其单位： Yun Zhou（西南大学地理科学学院）

通讯作者及其单位： Hong Yang（雷丁大学地理与环境科学系）& Qingyuan Yang（西南大学地理科学学院）

文章发表期刊： 《 Science of the Total Environment 》（中科院1区Top期刊|最新影响因子：9.8）

期刊平均审稿周期： 2.4个月

文章关键词： 热浪; 极端高温; 超热因子; 热指数; 风险分析; 脆弱群体; 谷歌地球引擎

文章摘要

图文摘要

由于气候变化，全球范围内的热浪已经加剧，对健康带来了巨大的风险，尤其是对老年人口。然而，在中国，有限的研究采用热指数来解读热浪的时空趋势以及其对老年人口的影响。通过比较三种热浪定义，本研究旨在利用过剩热量因子（EHF）评估1964年至2022年中国各地热浪的长期时空变化。该研究利用谷歌地球引擎（GEE）平台上的高分辨率再分析温度数据，有效地计算了热浪。该研究的结果显示，中国约77%的总面积的热浪频率和持续时间显著增加，华南地区经历了最频繁和最长的热浪。相反，在大多数地区，最大和平均热浪强度的增长趋势不明显。受热浪影响的老年人口总数从2001年的约1196万增加到2020年的超过3031万，预计全国每年有额外112万老年人暴露于热浪之下（R²=0.60，p<0.05）。人口因素对热浪暴露的影响最大，其次是气候效应和综合因素，分别解释了42.84%、34.85%和22.31%的方差。这些个体主要居住在中国东北、西南和华南地区。该研究还发现了沿海拔和土地利用类型的热浪暴露的地理变化。这些观点强调了制定战略干预措施以减轻热浪暴露带来的健康威胁的迫切必要性，特别是对中国的易感人群，如老年人。

研究背景及目标

研究背景

热浪是公认的天气灾害之一，被广泛认为是快速气候变暖的结果。自20世纪中叶以来，全球年热浪天数已经增加，未来几十年热浪预计将变得更加频繁和强烈。尽管有大量基于历史记录和未来模拟的研究强调了热浪趋势的增长，但热浪的普遍接受的定义仍然难以界定，并且在不同的研究领域和目标之间存在差异。传统上，热浪被定义为连续至少三到五天的异常炎热天气，其中平均或最高温度超过了当地温度分布的第90位、95位或99位百分数阈值。由于传统热浪研究中缺乏标准化的定义，一些热指数被用来表征热浪事件，如 Wet Bulb Globe Temperature (WBGT),Universal Thermal Climate Index (UTCI)以及Excess Heat Factor(EHF) 。尽管这些指数在监测和评估极端高温事件方面被广泛使用，但在中国，它们的应用仍处于起步阶段，只有少数几项研究利用这些指数来确定热浪。

超热因子（EHF）作为主要的热相关指数，考虑了短期和长期气温异常，因此能更严格、科学地界定热浪。多项研究已利用EHF准确预测和识别热相关死亡。澳大利亚气象局采用EHF对热浪强度进行分类和预测，因其能结合当地气候变异和适应性。借鉴澳大利亚的经验，强调在中国检测热浪中使用EHF的重要性。过去中国的热浪研究采用了各种定义，但地理范围有限，主要依赖气象站观测数据，缺乏全国范围的研究。大部分研究依赖于站点观测数据，尽管这些数据通常可靠，但存在空间覆盖有限和站点间差异大的限制。本研究旨在利用再分析数据进行热浪分析，这些数据在空间和时间上覆盖更一致，并且可以通过谷歌地球引擎平台轻松访问，提高了数据处理的效率。

广泛且加剧的极端高温事件对人类身体和心理健康产生了不利影响。大量流行病学研究证实，暴露于高温下会导致死亡率和发病率上升。脆弱人群，尤其是老年人，面临更严重的健康影响，因为他们的热浪应对能力较弱。随着中国老龄化人口的增长，了解和解决老年人暴露于热浪的健康风险至关重要。然而，在中国全国范围内了解老年人暴露于热浪的情况仍存在显著的研究空白。

表1.中国热浪研究

研究目标

本研究的主要目标是计算1964年至2022年在格网级别上的EHF，分析基于EHF定义的热浪的时空变化，并评估2001年至2020年老年人暴露于热浪的情况，为后续研究和政策制定提供有价值的见解。

数据与方法

研究区域

本研究聚焦于中国，因其独特的地理和人口因素相互作用，使其成为热浪探索的有趣区域。中国因其辽阔的面积和独特的地理位置呈现出多样的气候和地形。该国通常被划分为34个省级行政单位，进一步分为七个地理区域。中国的温度分布呈现明显的纬向梯度，不同地区气候各异，为研究者提供了研究热浪的宝贵机会。作为一个发展中国家，中国对气候变化的影响较为敏感，老龄化人口的趋势和热浪频率的增加进一步加剧了这种脆弱性。探索中国热浪的动态有助于了解国家对这些高温事件的适应能力，为制定灵活的适应策略和政策提供指导。

图1.（a）1964年至2022年中国暖季（5月至9月）的平均2米气温，（b）中国的地形图，以及（c）中国的七个地理区域

数据来源

（1）温度数据

本研究选用了欧洲中期天气预报中心（ECMWF）提供的ERA5-Land数据集，该数据集具有较高的空间分辨率（约为0.1°，相当于约11公里），能够更准确地反映中国地区的气温情况。该研究对该数据集的准确性进行了验证，结果显示在2388个气象站收集的2022年夏季的日温度观测数据中，平均皮尔逊相关系数（R）达到0.95，平均均方根误差（RMSE）为1.72℃，平均绝对误差（MAE）为1.46℃，反映了其较高的准确性。该研究主要基于谷歌地球引擎（GEE）平台进行，充分利用了ERA5-Land数据集。研究时段选择了1964年至2022年的暖季（5月至9月），以符合国际标准，确保了研究结果的可比性。此外，该研究还补充使用了位于中国重庆市北碚区的槽上站的平均温度数据，以更全面地分析中国地区的气温情况。

表2.本研究用到的数据集

（2）人口数据

在该研究中，使用了来自LandScan数据集的格网人口数据，该数据集覆盖了2001年至2020年的中国范围。这个数据集具有年度时间分辨率和30弧秒的空间分辨率（约1公里）。该研究从人口普查年鉴中获取了每个省份的老龄化率（即65岁及以上的人口比例）。通过将总人口乘以老龄化率，估算了每个格网的老年人口分布，假设每个省内老龄化率分布是均匀的。

（3）高程和土地利用数据

利用高程和年度土地利用数据来评估老年人口在不同海拔和土地利用类型下对热浪的不同暴露情况。这两个因素对热浪的影响显著。该研究采用了NASA于2020年完成的高分辨率数字高程模型NASADEM和中分辨率成像光谱仪（MODIS）土地利用数据。为了保持一致的空间尺度，该研究使用了最近邻插值方法将其他数据集的分辨率与温度数据对齐，以便更准确地分析老年人口在中国各地对热浪的暴露情况。

超热因子计算

EHF计算包含三个关键步骤，使用方程式1、2和3来表示。首先，需要计算两个指标：EHI sig（过超热因子-显著性）和EHI accl（超热因子-适应性）。

1.计算EHI sig：首先，计算最近三天的平均温度（T i ，T i+1 ，T i+2 ）。然后，从历史时期（1964年至1993年）的95th百分位温度（T95）中减去这个平均温度，以作为长期极端高温事件的基准。

2.计算EHI accl ：这个指标涉及两个时间段的平均温度。首先，计算最近三天的平均温度（T i ，T i+1 ，T i+2 ）。然后，从最近30天的平均温度中减去这个平均温度，以捕捉人口对短期温度变化的适应情况。

3.计算EHF：最后，通过将EHI sig 乘以EHI accl 和1之间的最大值来获得EHF。这一步骤将热事件的显著性与人口适应能力综合起来，提供了对热浪影响的全面衡量。

以上三个式子中，T代表温度（单位：摄氏度），而EHF代表热指数（单位：摄氏度的平方）。这些步骤的执行可以帮助我们更好地评估热浪事件对人群的影响，并采取相应的防范措施。

热浪的定义与特性

为了本研究的目的，该研究将热浪定义为至少连续三天的EHF超过零的时期。利用这一定义，对网格水平进行了热浪的年度分析，涵盖了热浪数量、持续时间、频率、振幅和强度等五个方面（见表3）。此外，Alexander和Perkins（2013年）提出了一个系统的框架来衡量热浪，包括三种定义，即基于EHF的热浪、基于TX90的热浪和基于TN90的热浪。基于TX90和TN90的热浪被定义为至少连续三天的时期，其中每日的最高和最低温度在一个中心为15天的窗口内超过了当地第90百分位数（1964年至1993年）。该研究在图S4中展示了基于网格的平均温度（Tmean）、最高温度（Tmax）和最低温度（Tmin）的第95和第90百分位数的三个地图。对这三种热浪定义在两个空间分辨率下进行了比较分析：网格水平和站点水平，时间跨度为2022年的暖季。中国气象局确定2022年是自1961年以来中国最热的夏季，导致大量热源性疾病和死亡事件（Ji，2022年）。因此，该研究的研究重点放在了2022年的数据上。

表3. 本研究中热浪的属性

人口暴露和趋势分析

在该研究中，通过使用11公里的地理网格尺度，在2001年至2020年期间计算每年的热浪暴露情况。在这两个十年中，中国经历了快速的城市化和社会转型。在这些变化的背景下理解热浪有助于阐明环境和社会因素之间的复杂相互作用。同时，高空间分辨率的人口网格数据可以从2001年到2020年获得。对于每个网格单元和每一年，将热浪天数乘以老年人口数量。然后将这些计算结果在所有网格单元中进行汇总，以估算国家级的热浪暴露水平。此外，该研究采用了Jones等人（2015年）和Nishant等人（2022年）提出的方法，特别是与评估气候条件和人口统计学对热浪暴露的影响相关的方法。我们将总体变化分解为气候、人口和综合效应。气候效应指的是热浪天数变化对人口暴露的影响。人口效应指的是人口规模和分布变化对风险人口的影响。综合效应表示气候变化和人口结构变化对热浪暴露的交织影响。通过将总体暴露变化分解为这三个因素，我们可以更好地理解每个因素的相对贡献以及它们如何相互作用来推动观察到的变化。

在方程式（4）中，EPE表示每年的总老年人口暴露，HWF表示每年的热浪天数总和，EP表示65岁及以上人口的数量。在方程式（5）中，ΔExposure是总暴露变化，计算方式是2001年与随后几年（从2002年到2020年）之间的差异。HWF base 和EP base 表示2001年的热浪天数和老年人口，而△EP和△HWF表示相对于2001年基准年的后续年份中老年人口和热浪天数的变化。因此，人口效应（HWF base ×ΔEP）、气候效应（ΔHWF EP base ）和综合效应（ΔHWF×ΔEP）共同构成总暴露变化。

此外，该研究利用非参数的Mann-Kendall检验和Sen斜率来识别热浪的时空趋势。这种方法计算效率高，对测量误差具有强大的鲁棒性，确定了所有成对斜率估计的中位数。Sen的Kendal斜率估计器经常用于长期时间序列数据的趋势分析中。在本研究中，统计显著性水平为5%，由|z|≥1.96的阈值确定。Z≥1.96表示显著增加的趋势，而Z ≤ −1.96表示显著减少的趋势。

(6)

这里的Y j 和Y i 分别代表时间tj和ti处的数据值，其中 t j >t i 。

需要注意的是，由于特定情况，香港、澳门和台湾的老化率和观测温度数据要么不可用，要么与其他地区不直接可比，因此它们被排除在的计算之外。所有与热浪相关的计算都是在GEE上进行的，这是一个以其丰富的数据集和强大的云计算能力而闻名的在线平台。主要代码是开源的，可供教育和学术目的使用。所有地图均使用ArcGIS Pro 3.0.2生成。

研究结果

热浪定义的比较

1.在格网尺度上对比

该研究在2022年暖季基于三种定义分析了热浪的五个方面（HWN、HWF、HWD、HWA和HWM）（图2–4）。使用EHF进行热浪计算，确定了2022年的10次热浪事件高峰。这个数字明显高于TX90（6次事件）和TN90定义（5次事件）确定的数字（图2 a1-a3）。观察到HWF具有明显的区域分布模式和显著的区域变化（图2 b1-b3）。TX90和TN90定义通常识别出持续时间较短的热浪，主要集中在四川、重庆以及长江中下游地区（图2 b2-b3）。相反，使用EHF计算，热浪通常持续超过60天，并且呈现出更广泛的地理分布（图2 b1）。对于热浪的最长持续时间，EHF方法（64天）比TX90方法（80天）和TN90方法（77天）短（图2 c1-c3）。这种变化可能是因为EHF方法识别了更多的热浪事件，因此产生了相对较短的最长持续时间。

热浪的幅度和强度是热浪强度的关键指标。比较EHF、TX90和TN90方法确定的强度，EHF计算得到的强度，以摄氏度平方（°C²）表示，通常超过了TX90和TN90方法的强度，两者以摄氏度（°C）表示。这种区别是因为EHF考虑了EHI因子的乘积（Nairn和Fawcett，2014；Oliveira等人，2022）。EHF方法得到的最高值集中在西藏、新疆、青海、南部内蒙古以及四川和重庆的交汇处（图2 d1）。相反，TX90和TN90方法显示出类似的空间模式，TN90的高强度主要观察到在四川和重庆之间（图2 d3），而TX90的强度延伸到长江中下游地区（图2 d2）。基于EHF的热浪显示了从北向南强度递减的趋势（图2 e1）。TX90计算显示从中部地区开始向北部和南部延伸的衰减（图2 e2），而在TN90定义下，高强度区域主要集中在青海、四川东部和重庆西部（图2 e3）。

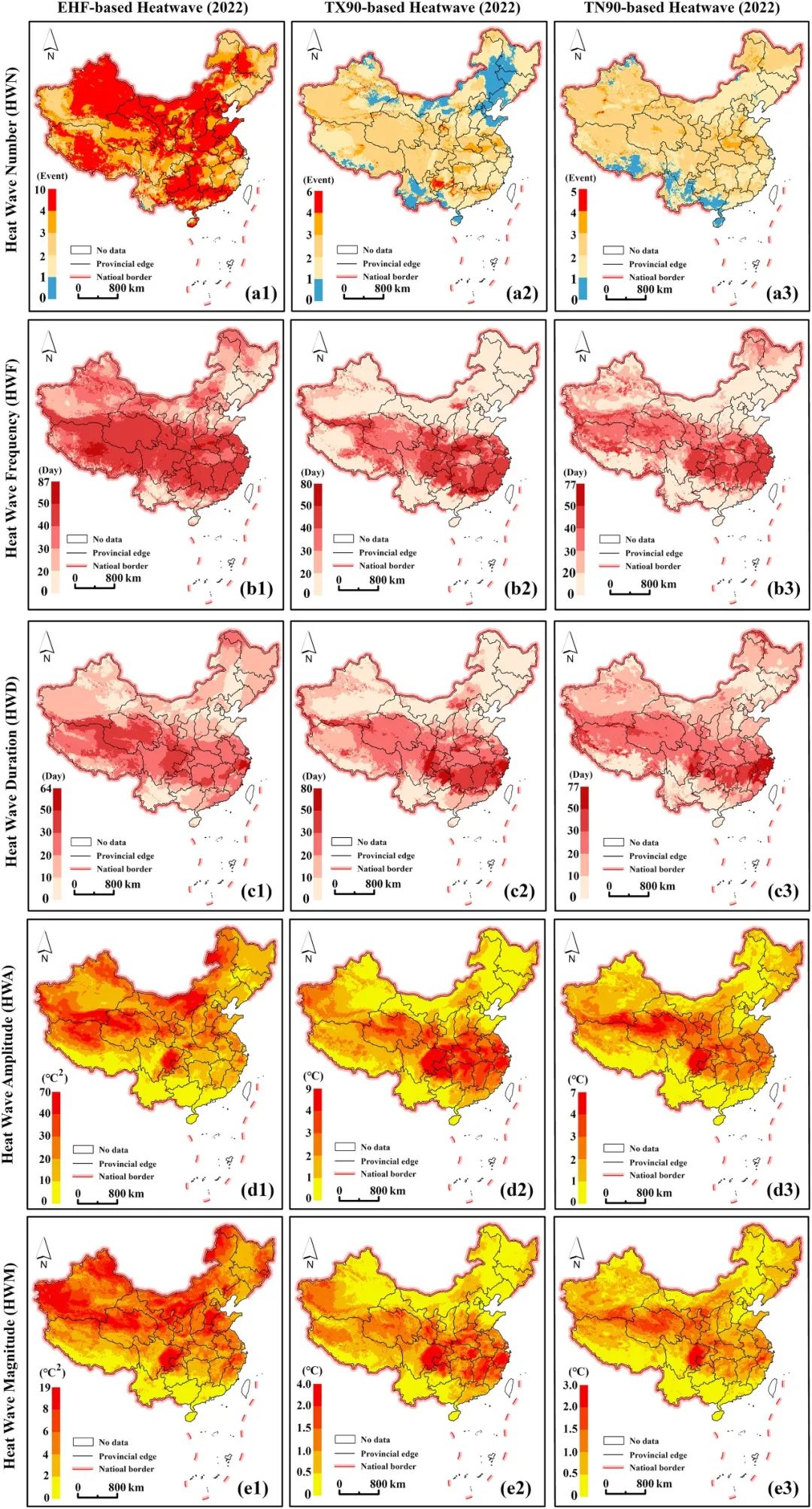
图2. 使用ERA5时间序列数据以及EHF、TX90和TN90方法在2022年暖季期间推导的热浪指标的比较：(a1-a3) HWN，(b1-b3) HWF，(c1-c3) HWD，(d1-d3) HWA，以及 (e1-e3) HWM。

2.站点水平的比较

该研究以槽上站为案例研究，解释了极端高温日（EHF）计算过程（图3）。该站位于海拔591米处，在2022年夏季记录了一次重大的热浪事件。7月和8月的平均日温度超过30摄氏度，最高日温度超过40摄氏度。

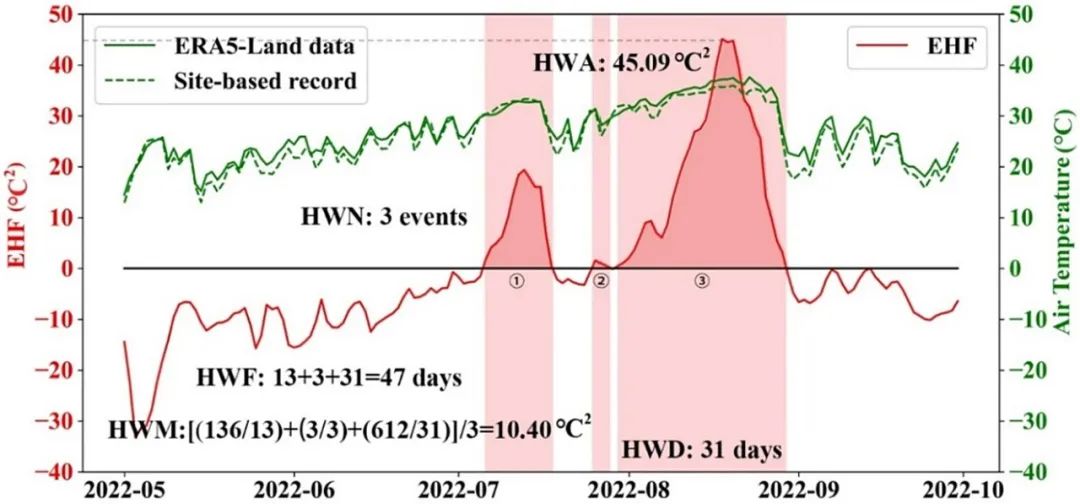
图3. 示意图展示了2022年暖季在Caoshang站基于EHF的热浪情况。红色实线代表每日EHF曲线，红色阴影标示热浪期间。黑色文字说明了五个热浪特征的计算来源。绿色实线对应于ERA-Land再分析的每日平均温度数据，而绿色虚线表示站点观测到的每日平均温度。两个温度数据集之间显著的一致性（R² = 0.99，p < 0.05）强调了再分析数据的可信度。红色和绿色实线的交点说明了使用观测和再分析温度数据进行EHF计算的过程。

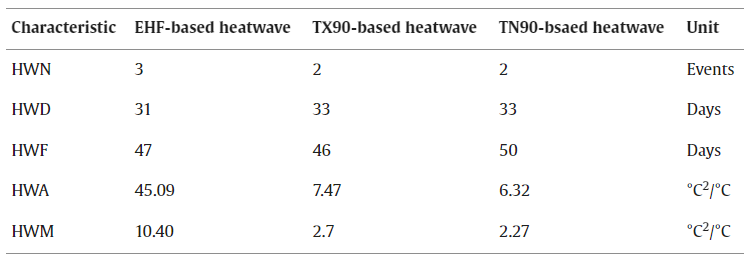
为了更全面地分析热浪特征，该研究同时使用了三种不同的定义来检验槽上站的2022年热浪数据。EHF方法识别出了三次热浪事件（图4），而TX90和TN90方法都只检测到了两次。在TN90定义下，单次热浪的最大持续时间和总热浪日数略多于EHF定义。根据TX90定义，单次热浪的最大天数略长于EHF定义，而整体热浪长度略短。然而，TX90和TN90方法计算的热浪强度一般低于EHF方法（见表4）。为避免单一站点比较的局限性，该研究将分析扩展到包括来自不同地理区域的另外八个气象站。EHF定义识别出了更多热浪事件，并显示出比基于TX90和TN90的更大变化的热浪强度。因此，EHF定义被发现更敏感地捕捉到了热浪事件的变异性和强度。

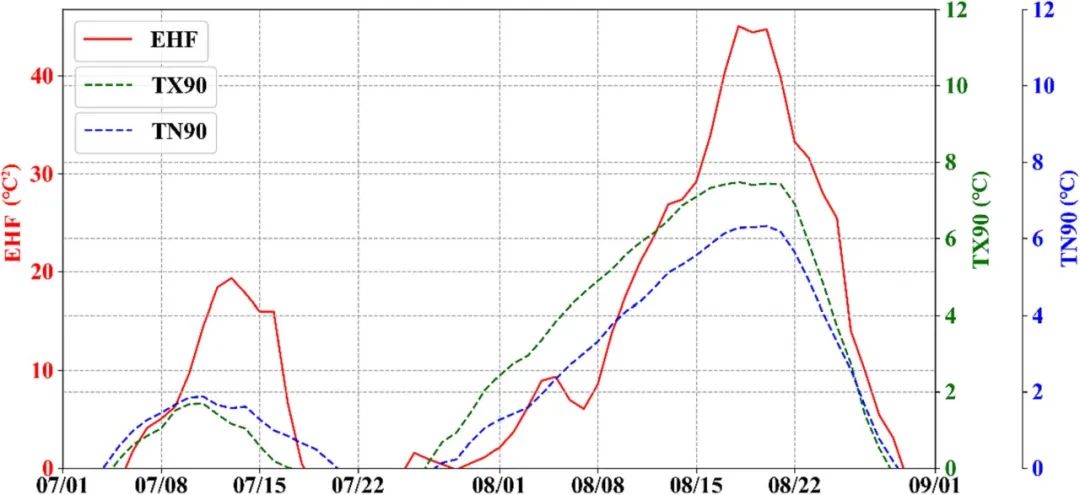
图4. 使用EHF、TN90和TX90在Caoshang站计算的不同热浪事件，时间跨度为2022年的暖季。

表4. 槽上站三种热浪定义的热浪特征。

热浪属性的变化

研究根据EHF指数制作了1964年至1993年和1994年至2022年的热浪气候学地图，并计算了其对应的百分比异常。热浪特征包括HWN（最长持续时间）、HWF（热浪频率）、HWD（热浪持续时间）、HWA（热浪强度）和HWM（热浪最大持续时间）（图5）。选取1993年作为基准年，划分了这两个时期，因为气候研究者经常将热浪分为不同时期进行比较分析。1993年结束了一个被广泛认可的30年基准期，从1964年到1993年。表格5总结了每个区域热浪属性的平均值和十年线性趋势。图6展示了从1964年到2022年热浪属性的Mann-Kendall趋势分析结果。

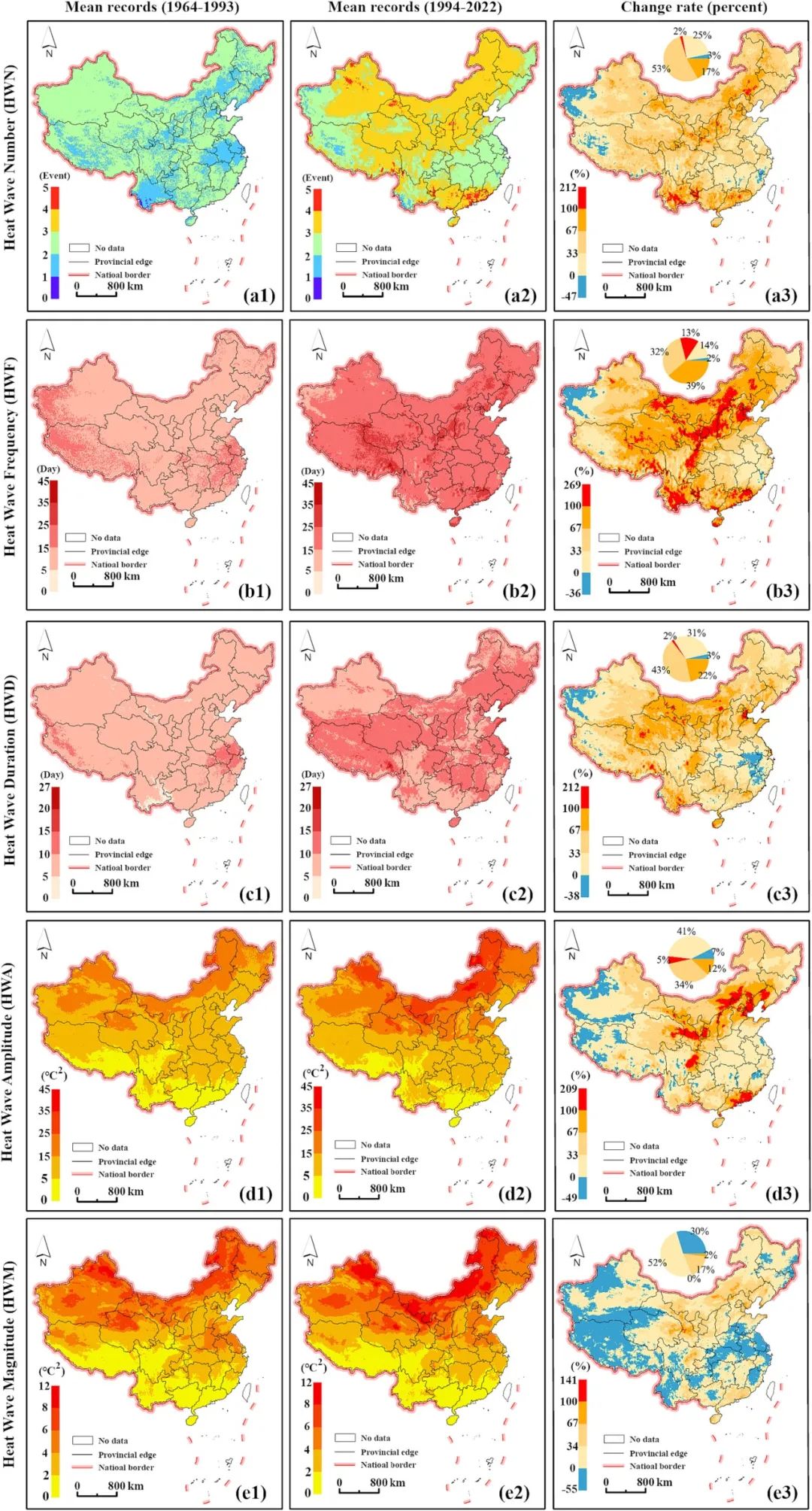
图5. 基于EHF的热浪属性的气候学（1964年至1993年和1994年至2022年）和异常（百分比差异）：(a1-a3) HWN, (b1-b3) HWF, (c1-c3) HWD, (d1-d3) HWA, 和 (e1-e3) HWM。

图5. 该地区热浪属性的平均记录和变化幅度

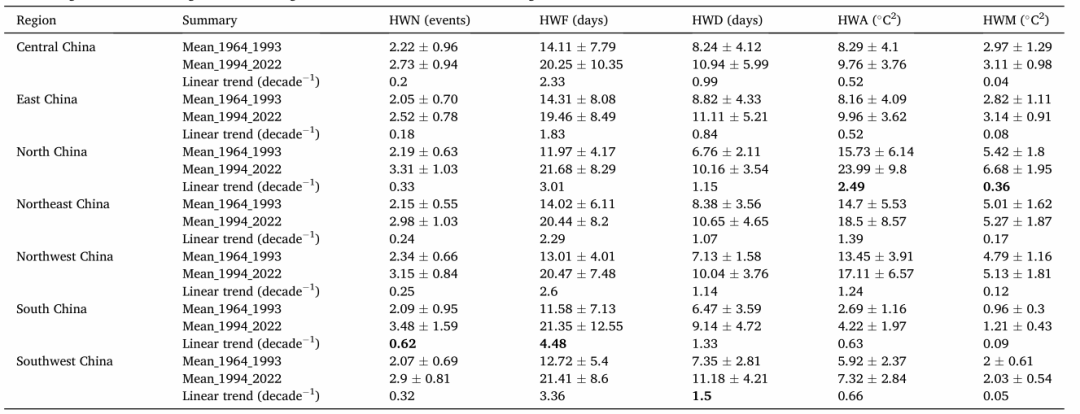
注:粗体文字表示中国七个地区热浪属性变化速率最大。

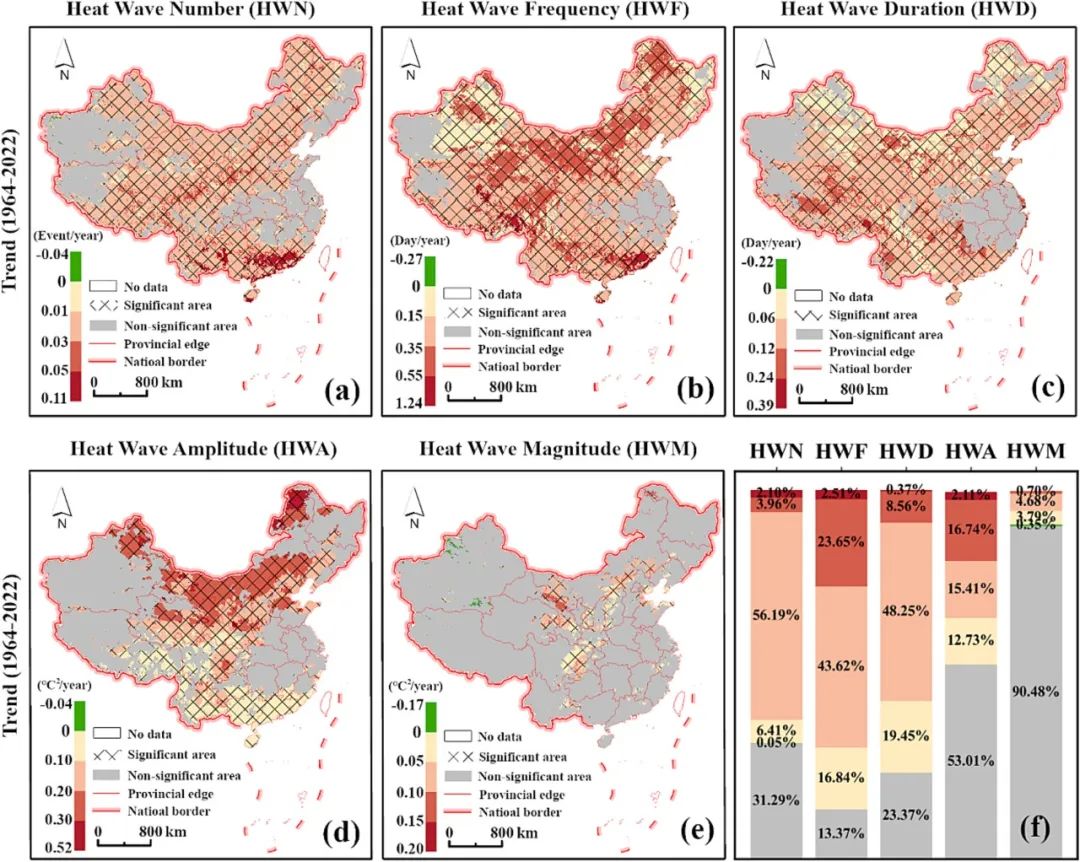
图6.从1964年至2022年，中国热浪属性的年度变化：(a) HWN, (b) HWF, (c) HWD, (d) HWA, 和 (e) HWM。颜色条显示了线性变化率，采用Sen的斜率方法进行估计。带有斜纹图案的区域强调了在95%置信水平下，Mann-Kendall检验指示出的显著趋势。最后的条形图 (f) 显示了Sen的斜率估计的显著 (彩色) 和非显著 (灰色) 像素的百分比。

在中国，自1964年至1993年，高温天气事件的频率和持续时间呈逐年增加趋势，尤其是在1994年至2022年期间，这种增加趋势更为显著。虽然大部分地区都显示出增加的趋势，但新疆和西藏等少数地区却呈现出下降的趋势。热浪的持续时间和强度也在增加，其中华南地区的变化最为显著。与此同时，热浪的强度在纬度上呈现出明显的梯度，从南向北逐渐增加。在分析了不同地区每个十年内的线性趋势后发现，华南地区的热浪频率和持续时间变化最为显著，而华北地区的热浪强度增加率最高。

在研究期间，中国的高温天气指标显示出普遍的增加趋势，其中高温天气次数、频率和持续时间在绝大多数地区呈显著上升趋势。尤其是南部、西部和北部地区的增加最为明显。然而，高温天气强度的增加并不如其他指标那样普遍，而是集中在部分地区。

老年人口暴露于热浪

1.时空趋势

从2001年到2020年，我们对中国老年人口在高温天气中的暴露情况进行了格网尺度的分析（图7）。在这段时间内，高温天气持续时间的平均值从每年0天到45天不等。值得注意的是，在中国南部、东北部和西南部的西部地区，我们观察到了明显的增加趋势，这些地区占据了中国总土地面积的四分之一。中国老年人口的分布呈现出明显的空间异质性，南部和东部地区的集中度较高，而西部和北部地区则相对稀疏。华东、华中和西南部分地区的老年人口呈现出增长趋势，占据了中国总土地面积的22%。高温天气持续时间的增加以及老年人口的增长显著增加了他们对高温天气的暴露。中国约31%的地区显示老年人口对高温天气的暴露呈显著增加趋势，尤其是东北部、西南部和华南地区。相反，约4%的地区显示明显的下降趋势，主要集中在东北部和西北部地区。这种下降可能归因于人口减少和高温天数减少。

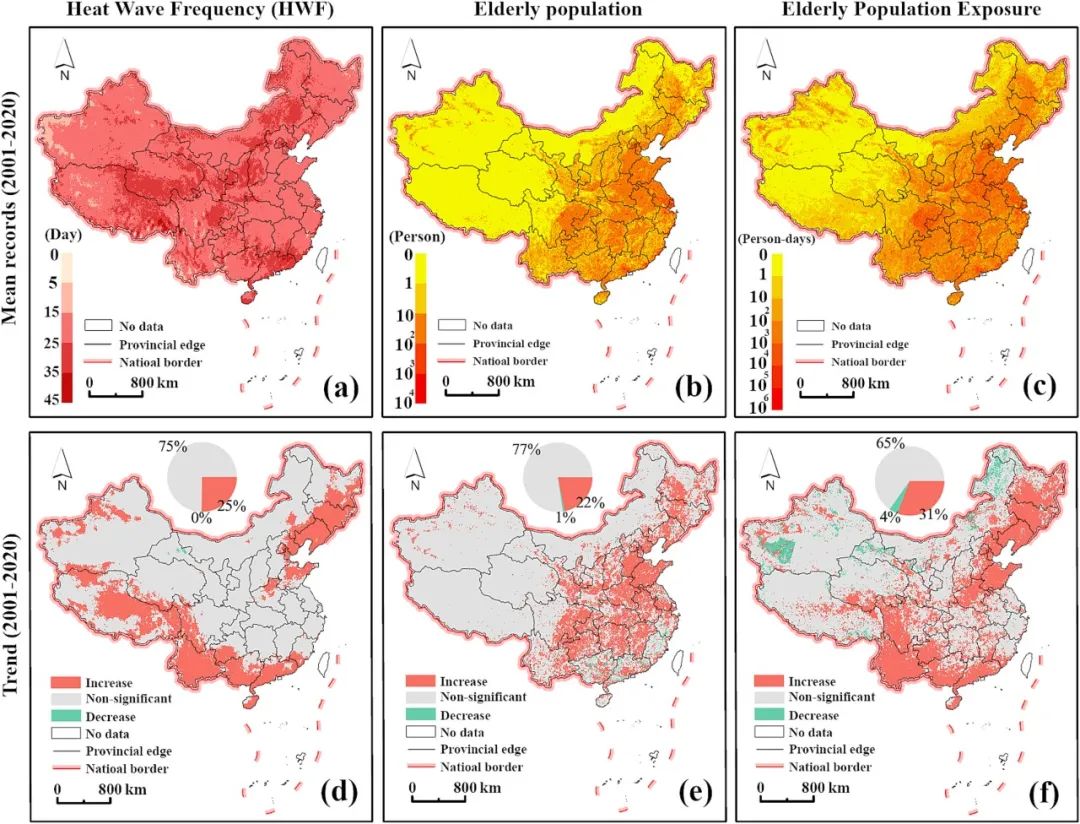
图7.从2001年到2020年，详细说明了热浪频率指数（HWF）、老年人口数量和老年人口暴露于热浪的年均值（a-c）和Sen斜率趋势（d-f）地图。

2.地理格局

该研究还对老年人口在2001年至2020年期间在高温天气中的地理变化进行了综合分析，考虑了经度、纬度、海拔和土地利用模式等因素（图8）。在经度方面，高温天气影响老年人的分布从西向东扩展，主要位于东经100°至130°之间。纬度变化表明，暴露程度从北向南增加，主要在北纬17°至25°之间。海拔方面的分析显示，海拔增加会降低老年人对高温天气的风险。在海拔0至200米的平原地区，每个网格每年平均有875名老年人受影响，而海拔高于2500米的地区，每个网格每年平均只有6名老年人受影响。此外，我们比较了城市和建设用地区域与其他土地利用类型中老年人对高温天气的暴露情况。结果显示，在城市和建设用地区域中，受影响的老年人口数量远高于其他地区。通过线性回归模型的分析，我们发现老年人口每年受影响的数量呈显著增加趋势，尤其是在城市和建设用地区域。

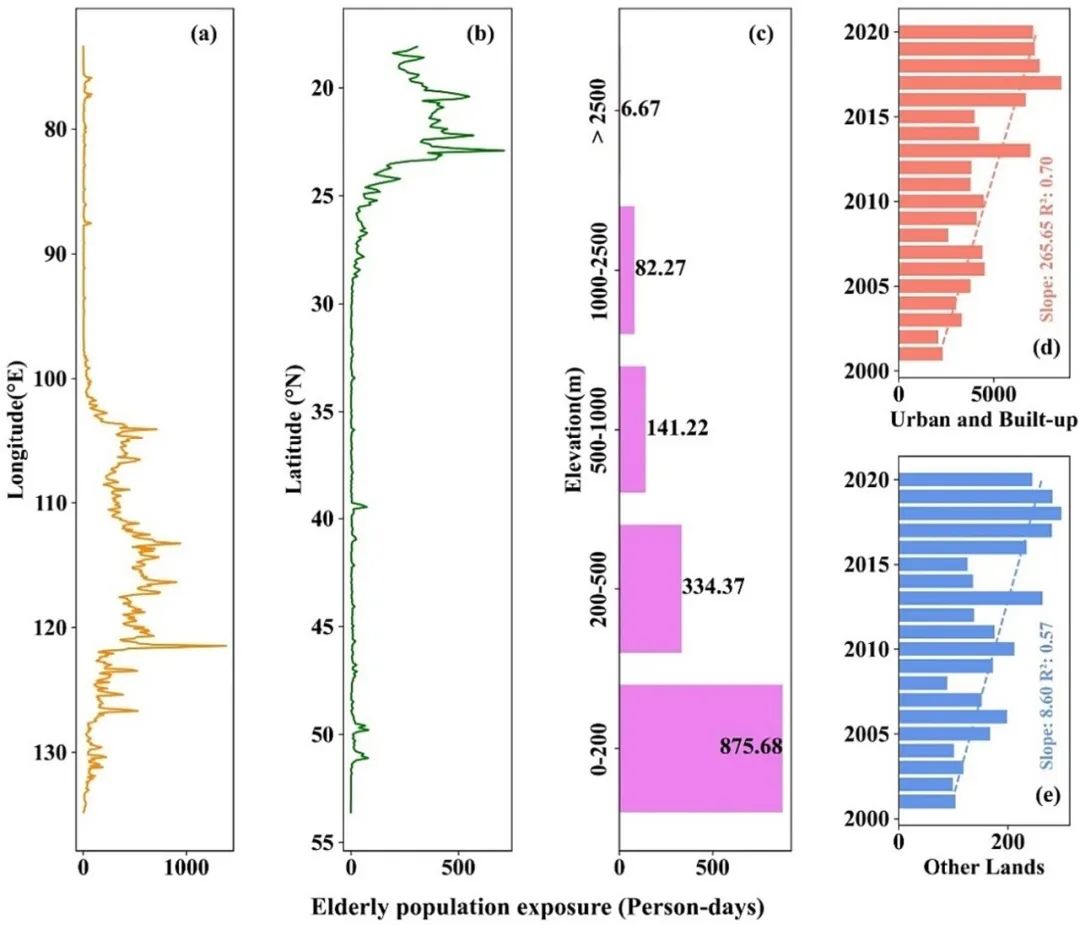
图8.老年人口暴露于热浪的地理模式，沿着不同因素展现：(a) 经度梯度，(b) 纬度梯度，(c) 海拔梯度，(d) 城市和建成区，以及 (e) 其他土地利用，跨越2001年至2020年。

3.暴露的分解

该研究利用2001年的老年人口暴露数据作为参考，深入探讨了全国范围内气候、老年人口的人口结构变化，以及它们对热浪暴露的交互作用的影响（图9）。在20年的时间里，受热浪影响的老年人口数量急剧增加，从2001年的11,963,100人增加到2020年的30,311,770人，比2001年基准增长约153％（见图9b）。年均增长约为1,119,545人（R²= 0.60，p<0.05）。分解气候、人口变化及其相互作用对热浪暴露的影响，该研究观察到每个因素的不同影响。虽然热浪日数总体呈上升趋势，但2013年和2018年等年份的热浪特别严重。气候变化单独导致每年约有390,124名老年人受热浪影响的增加（R²=0.25，p<0.05）。过去20年中老年人口的显著增长，可能是由于预期寿命增加，导致每年额外有479,580名老年人暴露于热浪中（R²=0.88，p<0.05）。气候变化和老年人口的不断增长共同导致估计每年有245,558名老年人受热浪影响的增加（R²=0.44，p<0.05）。总而言之，在2001年至2020年期间，气候效应（由于温度变化引起）占热浪影响老年人口增加的约34.85％，而人口效应（由于人口动态变化，如老龄化或增长）占约42.84％。其余的22.31％来自这些因素之间错综复杂的。

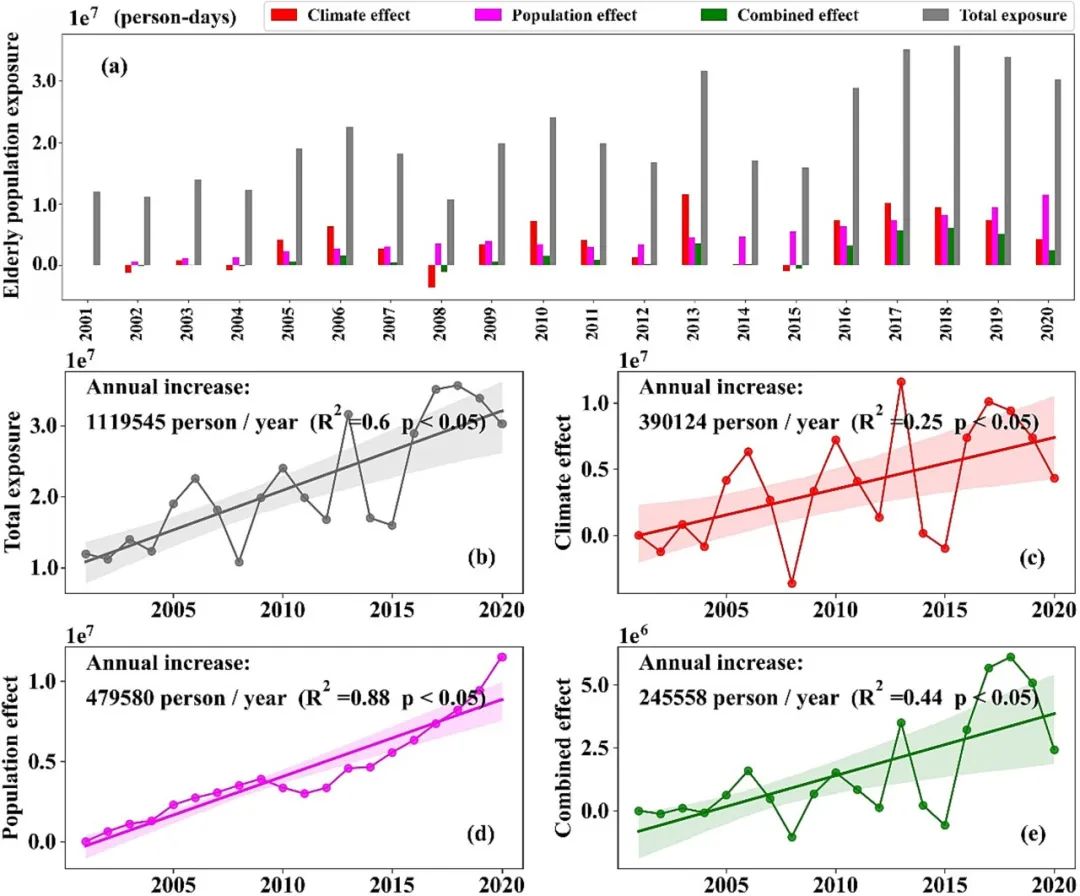
图9.(a) 对中国2001年至2020年老年人口的年度总体暴露进行分解。(b) 总老年人口暴露的线性变化，(c) 气候影响引起的线性变化，将2001年老年人口保持不变，(d) 人口影响引起的线性变化，将气候保持在2001年水平，(e) 组合效应引起的线性变化。实线表示线性趋势，而回归线周围的半透明带表示回归估计的置信区间（p < 0.05）

研究讨论

热浪时空趋势

该研究对热浪的影响进行了深入探究，主要分析了其空间和时间趋势以及与公共健康的关系。在定义热浪方面，该研究采用了EHF、TX90和TN90等指标，综合考虑了热浪的严重程度和当地气候条件，特别关注了老年人群体的暴露情况。通过与其他定义进行比较分析，该研究发现EHF能更准确地捕捉热浪事件，尤其是持续和强烈的情况。利用长期数据，我们发现近六十年来中国热浪频率和持续时间明显增加，尤其是在南部地区。然而，热浪的强度变化不显著，可能受当地气候影响。人口暴露于热浪的趋势与相关死亡数据相符，2013年和2017年的暴露水平明显增加。通过对比不同年份的热浪频率和区域分布，该研究验证了EHF方法的可靠性和适用性。这些发现强调了热浪对公共健康的重要性，以及在研究和应对热浪时考虑地区气候特征的必要性。

Sci. Total Environ | 中国热浪和老年人口暴露的时空变化

正文

(adsbygoogle = window.adsbygoogle || []).push({}); 第一时间获取气象科研资讯 『 气象学家 』 公众号 交流群 加入

请到「今天看啥」查看全文

第一时间获取气象科研资讯

『气象学家』公众号交流群

加入