你相信这些数学事实么?(上)
1、三门问题(蒙提霍尔问题)
假如你正在参加一个节目。主持人给了你三扇门,其中一扇门里面是一款崭新的汽车,另外两扇门里面都是一只羊。你选择了其中一扇,然后,主持人打开你未选的另外两扇门里是羊的那一扇,然后——
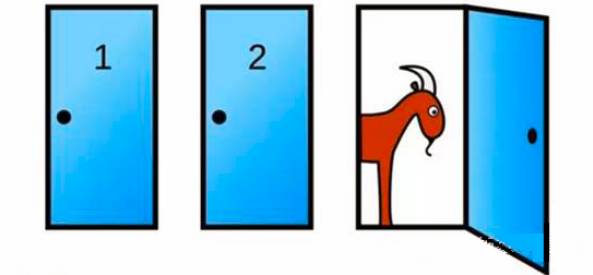
主持人问你:你是否要换一扇门?还是就要你刚才选的那一扇?
你会怎么做?
你第一反应一定是就要你刚才选的那一扇。
到目前为止,一切都没有问题,对吧?
因为现在只有两扇门了,你可以推断出,有一半的机会赢得那辆车。对吗?

你错了??
这个游戏的最佳策略就是
“换门”
,每次都换。
如果你每次都换,只有当你第一次选的那扇门里就是车的时候你才会输。
因为你第一次选中车的几率是1/3,而每次都换你输掉的几率也是1/3。
这就意味着,如果你每次都换的话,赢得几率就有2/3。
换门赢的几率是不换门赢的几率的两倍。
还不信吗?这么说吧,假如你选的是一号门,请看下面所有可能发生的情况:
如果你不换门,三种情况只有一种情况能赢;如果换门,就有两种情况能赢。
你还不信?
那我们换成50扇门再做一遍。你不选一号门。
我把其他是羊的48扇门都亮给你。对你的选择还那么有信心吗?别忘了:你第一次选对的机会只有1/50。道理完全是一样的。
2、
0.999...=1
无限循环小数0.999...等于1。
有许多的证法都可以证明这个等式,但仍然有很多的人纠结这个概念,下面就是一个很好的正面:
x=0.999...
10x=9.999...
10x-x=9.999...-0.999...
9x=9
x=1
很多人纠结这个理念的原因,是我们人类的思维很难去理解“无限”这个概念。在某种层面上,大多数人只是想象最终总会以一个“9”结束。
数字这东西总是换种方式表达就会看起来不大一样,当然这个也不例外。
这其中的原因是和“无限”与“有限”的概念紧密关联的,光这些就够我们大伤脑筋的了。
下面是另外一种证法:
1/3=0.333...
3×1/3=3×0.333...
1=0.999...
3、偶数和自然数一样多
偶数和自然数一样多。
表示事物个数的数叫做自然数,如1,2,3,4等等。
自然数的数量是无限的。偶数的数量也是无限的。
你或许会想象自然数要比偶数多,因为自然数由奇数和偶数组成。
那你就错了。
我们可以在自然数和偶数之间建立一个一对一的对应关联式,这个关联式将告诉你,每个自然数都有一个与其对应的偶数。
我们可以这样想:每个自然数都有一个等于它两倍的偶数,而每个偶数也都有一个等于它一半的自然数:
12
24
36
48
510
612
714
816
这是什么意思呢?
就是说,
每一个自然数,都有一个与之对应的偶数
。
这就是说,这两个无限集的大小是相等的,我们称之为
“可数无限集”
这就将其与“不可数无限集”如“实数集”或“复数集
”区分开了。
例如,我们不能再自然数和实数之间建立一个一对一的对应关联式。
其他的可数无限集还包括:有理数集合奇数集。
4、本福特定律
在实际的数字中,数字“1”作为首位数字出现的几率是30%.















