
文章链接:https://www.nature.com/articles/s41467-024-47903-3
摘要
低维材料的范德华 (vdW) 组装已证明能够创建具有按需特性的结构。据预测,vdW 封装可以引起几 GPa 的局部高压,这将强烈改变被捕获材料的结构和性能。在这里,我们报告了 vdW 封装引起的碳纳米管 (CNT) 的结构崩溃。通过简单地用六方氮化硼薄片覆盖碳纳米管,大多数碳纳米管(约77%)从管状结构转变为塌陷的扁平结构。无论其原始直径如何,所有塌陷的碳纳米管均表现出约 0.7 nm 的均匀高度,大致相当于双层石墨烯的厚度。拉曼光谱进一步证实了这种结构塌陷,拉曼 G 峰显示出显着的展宽和蓝移。局部 vdW 压力的分子动力学模拟完全捕获了 vdW 封装引起的 CNT 塌陷。进一步的近场光学表征揭示了伴随碳纳米管结构塌陷的金属-半导体转变。我们的研究不仅为基础研究提供了一种产生局部高压的便捷方法,而且还为纳米电子应用提供了塌缩碳纳米管半导体。
研究背景和主要研究内容
高压可以强烈改变材料的结构、物理和化学特性,因此成为材料科学,能源工程研究的有力工具、和生物医学。高压通常在大型压力机中产生,该大型压力机通过两个或更多个坚固的砧集中大的力来压缩样本。然而,对专用设备的需求严重限制了高压的应用。绕过该困难的一种方法是减少高压持续时间,即使用动态高压,这可以使用瞬态脉冲负载来容易地实现。另一种方法原则上是将高压区域缩小到纳米尺度,这样很小的力就可以产生非常高的压力,因为压力与加载面积成反比。
范德华 (vdW) 异质结构,即通过 vdW 力组装低维材料,近年来由于设计具有按需特性的新型材料的前景而受到广泛关注。 vdW 异质结构的独特特征之一是捕获材料上的纳米级局部高压,预计该高压为 GPa 级,实验观察到的值为 1.2 GPa 。这种通过简单地堆叠低维材料来产生局部高压的便捷方法被认为可以创造新的化合物并探索纳米材料的科学,例如低维材料中的超导性、相变和储氢器。
另一方面,碳纳米管的塌陷早已被发现。已经报道了用于诱导CNT塌缩的各种方法 ,例如施加静水压力 、使用电子束照射以及采用球磨 。最近,陈等人已经证明了利用金刚石砧和热处理产生的高压将碳纳米管塌缩成宽度小于 10 nm 的纳米带的能力。然而,有些方法在纳微米尺度上应用具有挑战性,而另一些方法则复杂且低效。此外,理论研究还提出了碳纳米管的详细塌陷相图,并确定了不同直径和壁厚的碳纳米管在不塌陷的情况下可以承受的压力范围。
在这里,我们证明了 vdW 封装产生的局部高压可以引起 CNT 的结构塌陷。通过简单测量纳米管高度,我们发现大多数六方氮化硼封装的碳纳米管(约77%)都发生了结构塌陷。拉曼光谱进一步证实了碳纳米管的塌陷,其中G峰从11 cm -1显着展宽至63 cm -1,蓝移为7 cm -1。我们的分子动力学 (MD) 模拟完全捕获了 CNT 的塌陷,表明 vdW 封装可以在纳米尺度上产生几 GPa 的局部高压。我们通过卢廷格液体等离子体的近场光学表征进一步观察了塌陷碳纳米管中的金属-半导体转变。我们的方法提供了一种简单的途径来制造带隙可调的折叠碳纳米管,并在电子和光电子学中得到实际应用。此外,vdW 封装可以作为一种简单的方法来产生几 GPa 的局部高压,用于探索纳米尺度的高压现象。
hBN 封装导致 CNT 塌陷
图 1a显示了SiO2基底上的六方氮化硼封装引起的CNT塌陷的示意图。单壁碳纳米管最初通过化学气相沉积在SiO2基底上生长,然后通过机械转移被六方氮化硼薄片覆盖。有关样品制作的更多详细信息,请参阅“方法”部分。由于粗糙的SiO2表面和六方氮化硼层之间的vdW吸引力和钉扎效应,当六方氮化硼薄片遇到CNT时,在六方氮化硼薄片中建立了大的拉伸应变。 hBN中的这种拉伸应变会对下方的 CNT 产生压力,导致 CNT 塌陷。
在实践中,我们选择典型厚度为 2 nm 的非常薄的 hBN 薄片来封装 CNT。这是为了避免厚的六方氮化硼掩盖后续碳纳米管高度和拉曼信号的测量。图 1b显示了通过原子力显微镜 (AFM) 测定的直径为 1.8 nm 的 CNT 的形貌。当CNT被hBN封装时,其高度从1.8 nm下降到0.7 nm(图 1c),推断CNT的结构崩溃。补充说明1中分析了六方氮化硼的结构弯曲对碳纳米管高度测量的影响 ,由于六方氮化硼的厚度较小,可以忽略不计。有关该样本的更多数据可以在补充说明2中找到 。我们测试了许多 CNT 样品,以及所有有和没有 hBN 封装的碳纳米管的高度。如图1d所示 ,没有六方氮化硼覆盖的碳纳米管的直径范围为1.0 nm至2.0 nm。有趣的是,在 hBN 封装区域,大多数 CNT 高度下降至 0.7 nm 左右,这与结构塌陷相对应。
拉曼光谱进一步证实了碳纳米管的塌陷。图 1e、f显示了在图1b所示的CNT的两个不同位置处获取的拉曼光谱 。图 1e显示了从圆形CNT(图1b中的紫色点)收集的拉曼信号 ,显示出尖锐的G峰,半峰全宽(FWHM)仅为11 cm -1。从塌陷的碳纳米管(图 1b中的蓝点)获取的拉曼光谱如图1f所示 ,它显示了几个不同的特征。首先,拉曼D峰出现在1330cm -1附近,表明结构缺陷的存在或新散射路径的激活41。 hBN 声子峰出现在 1360 cm -1附近,该峰来自封装的 hBN 层。其次,G峰的半高宽从11 cm -1增加到63 cm -1,表明碳-碳键共振频率的多样性,这为结构塌陷提供了明确的证据。第三,G峰也具有约7cm -1的蓝移。前面的实验4表明G带在低于4.0 GPa时以5.4 cm -1 GPa -1的速率发生蓝移。据此,我们可以通过比较 G 波段蓝移与暴露在 hBN 外部的 CNT 来估计 CNT 上的 vdW 压力。蓝移7.0 cm -1对应于1.3 GPa的平均压力。使用卷积模型,我们可以通过拉曼光谱估计高达 10 GPa 的 vdW 压力。更多拉曼数据和详细信息可以在补充说明 3和4中找到。
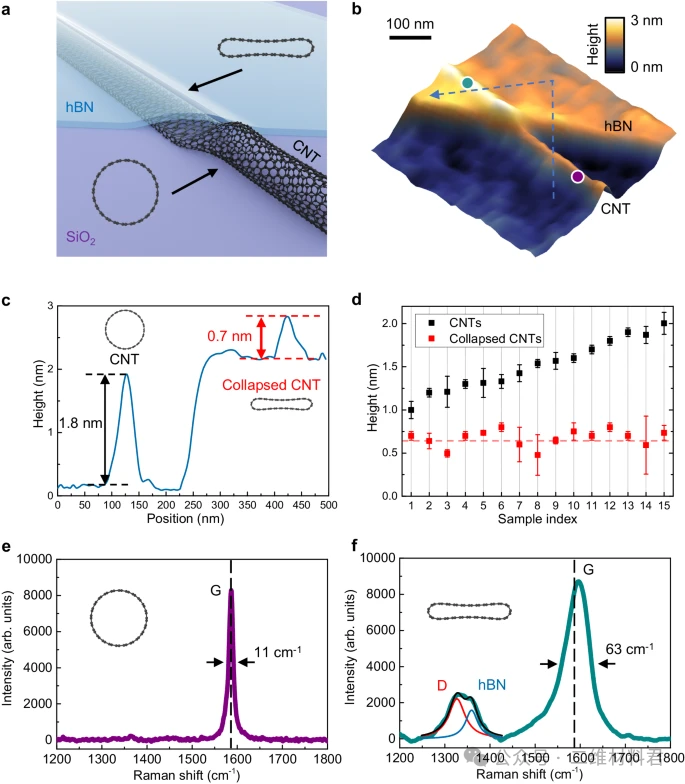
图 1:六方氮化硼封装的碳纳米管的结构塌陷。a SiO2基板上六方氮化硼封装的 CNT 挤压成塌陷 CNT 的示意图。b直径为 1.8 nm 的六方氮化硼封装的 CNT 的 AFM 形貌。c形貌线轮廓显示,h-BN 封装的高度发生显着变化。d有(红色方块)和没有(黑色方块)hBN 封装的 CNT 高度的统计。所有塌陷的碳纳米管,无论其初始直径如何,都表现出约 0.7 nm 的恒定高度。红色虚线代表塌陷碳纳米管的理论高度。误差线代表在同一碳纳米管的不同位置测量的五个高度值的标准偏差。e圆形 CNT(紫色曲线)和f hBN 封装的塌陷 CNT(绿色曲线)的拉曼光谱。虚线表示圆形碳纳米管的初始G峰位置。红线和蓝线分别是 D 和 hBN 面内声子峰的洛伦兹拟合。
局部高压的MD模拟与理论分析
为了了解高压的发生,我们进行了 MD 模拟。考虑到六方氮化硼和碳纳米管之间的微小不匹配会导致相当大的超级单元,我们用与碳纳米管具有相同晶格常数的石墨烯代替六方氮化硼,以节省计算消耗。补充图 6显示了由约 60,000 个原子的六方氮化硼封装的 CNT 的更准确的完全原子 MD 模拟,并得出相同的结果。图 2a显示了石墨烯封装的CNT的MD模拟的截面图。
在这里,我们设置直径为 1.8 nm 的 CNT,并固定底部石墨烯。我们在碳纳米管顶部添加三层石墨烯,并对顶部石墨烯中远离碳纳米管的一些原子施加向下的力。一旦上层石墨烯接近下层石墨烯,由于vdW相互作用,石墨烯层会自发地粘在一起,最终将CNT压缩成塌陷相并改变结构的高度。图 2b显示了作用在碳管下表面的层间vdW力和压力。注意到我们的 MD 模拟显示最大局部压力约为 10 GPa,这与之前的预测非常吻合。产生如此高压的原因可能是封装的2D材料薄膜可以有效地将向下的vdW力从较大的区域施加到非常局部的CNT上。
为了确保高度变化的贡献,模拟了不同直径的CNT,如图 2c所示。模拟结果表明,无论直径是多少,CNT在vdW层间相互作用下都会被严重压缩(图 2c)。上层原子的高度波动约为0.7 nm,这与AFM形貌结果(点)一致。这些模拟结果表明,即使是直径为 0.8 nm 的 CNT 也可以被压缩为层间距离为 0.34 nm 的完全塌陷相。塌缩相的临界直径从 5.1 nm 减小到 0.8 nm,这是由单向 vdW 压力而不是 Levy-Carrier 方程40中的各向同性均匀压力引起的,如补充说明7所示 。这些模拟结果以及补充说明 9中的额外模拟表明,vdW 压力导致的 CNT 塌陷在理论上是可能的。
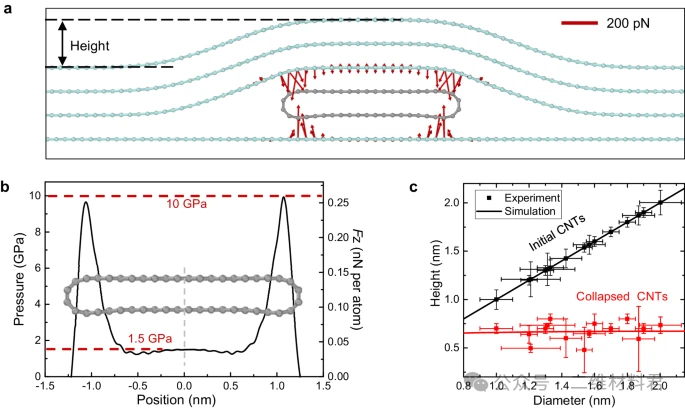
图 2:六方氮化硼封装的碳纳米管的 MD 模拟。MD 模拟的六方氮化硼封装的 CNT 的截面图。红色箭头代表原子上的力的方向,长度代表大小。绘图右上角箭头的长度代表 200 pN。b作用在 CNT 上的 vdW 压力/力的空间分布。c圆形碳纳米管(黑色)和六方氮化硼封装的塌陷碳纳米管(红色)的提取高度。直径为 0.8 nm 至 2.0 nm 的 CNT 在 vdW 压力下塌陷至 0.7 nm 左右。误差线代表同一碳纳米管不同位置的多个测量值的标准偏差。
CNT塌陷率统计
为了估计通过六方氮化硼封装而塌陷的碳纳米管的产量,统计了84个生长的碳纳米管和15个六方氮化硼封装的碳纳米管。图 3a、b显示了SiO2基底上生长的CNT和六方氮化硼封装的CNT的高度的分布直方图。图 3a显示了生长时 CNT 的高度分布,范围为 1 nm 至 2 nm。图 3b显示了六方氮化硼封装的碳纳米管的高度分布直方图,其中观察到直径显着减小。这里,小于0.9nm的高度被认为是塌缩相CNT。 hBN封装的塌陷CNT产率约为77%,这是一个相当高的塌陷率。由于六方氮化硼层中的应力分布不均匀,一小部分碳纳米管仍然存活。一种可用于提高塌陷率的可能方法是增加六方氮化硼层的厚度。我们的 MD 模拟表明,较厚的六方氮化硼薄片会导致较高的 vdW 压力和较高的塌陷率(更多详细信息请参阅补充说明 6和8)。此外,其他 2D 材料(例如少层石墨烯)的封装也可能导致 CNT 塌陷(更多详细信息请参阅补充说明 5)。
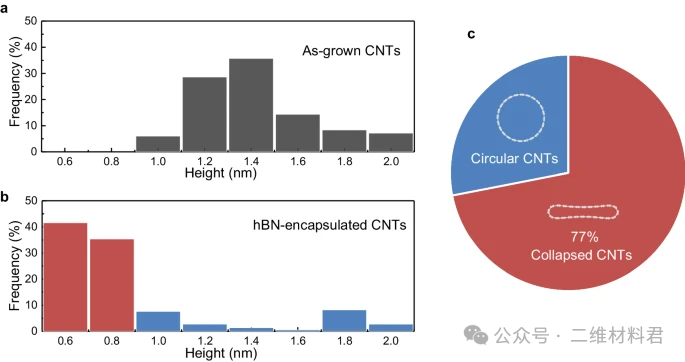
图3:vdW封装前后CNT高度的分布直方图。a , b分别为六方氮化硼封装之前 ( a ) 和之后 ( b )的 CNT 高度的分布直方图。 c塌陷率约为77%。该百分比是指折叠的碳纳米管与所有研究的碳纳米管之间的长度之比。
塌陷引起的金属-半导体转变
伴随着碳纳米管的结构塌陷观察到金属-半导体转变。通过CNT的Luttinger液体等离子体的近场光学表征,以实验方式揭示了CNT的金属-半导体转变。在这里,我们选择了一个在六方氮化硼覆盖区域既有塌陷部分又有圆形部分的特定CNT样品,这样我们就可以直接实现塌陷引起的近场光学响应变化。图 4a显示了不同栅极电压下CNT等离子体激元的近场光学测量示意图。波长 10.6 μm 的红外激光束聚焦在镀金的 AFM 尖端上,可以同时激发和探测 CNT 中的等离子激元(更多详细信息参见“方法”部分)。先前的研究分别报道了金属和半导体碳纳米管中的线性和非线性卢廷格液体等离子体。在金属碳纳米管中,等离子体激元波长是恒定的,与栅极电压控制的费米能级无关。而在半导体碳纳米管中,等离子体激元波长很大程度上取决于费米能级,并且可以通过栅极电压进行调节(更多详细信息请参阅补充说明 8中碳纳米管中等离子体激元的卢廷格液体理论)。
图 4b显示了封装的CNT的形貌以及不同栅极电压下封装的CNT中的等离子体激元的红外响应。显然,塌陷区域(上部)的光学响应比圆形区域(下部)低得多,特别是在电荷中性(V g = 0 V)处。此外,沿着纳米管可以看到周期性图案,这是等离子体干扰的结果。我们分别提取并绘制了图4e、g中本征区域和塌缩区域的等离子体线轮廓 。对于本征圆形区域,不同栅极电压下等离子线轮廓具有相似的幅度和周期(图 4e)。为了定量研究等离激元波长,我们将图4e中的线轮廓 与指数衰减正弦波函数进行拟合。提取的等离激元波长绘制在图 4f中,其中等离激元波长保持恒定值约65 nm,而与栅极电压无关。这些等离子体激元特征与之前报道的金属碳纳米管等离子体激元非常吻合。因此,我们确定圆形区域是金属碳纳米管。
相反,图 4g中塌陷区域的等离子体线轮廓随着栅极电压的变化而发生显着变化。当V g = 0 V 时,几乎没有近场光学响应。随着栅极电压的增加,近场光学响应以及等离子体激元波长增加。提取等离子体激元波长作为栅极电压的函数并绘制在图 4h中,其表现出强非线性Luttinger液体等离子体激元,与先前报道的半导体碳纳米管中的等离子体激元行为非常一致。因此,我们推断塌陷的部分是半导体的。除了上面介绍的例子之外,我们还在其他七个塌陷的 CNT 样品中观察到了金属-半导体转变,如补充图 9所示。
为了从理论上理解观察到的金属-半导体转变,我们对塌陷和圆形碳纳米管的能带结构进行了第一性原理密度泛函理论(DFT)计算,分别如图 4i、j所示。当塌陷时,碳纳米管的上壁和下壁接近约0.3 nm,具有哑铃结构,如图 2a所示。塌陷碳纳米管上下壁之间的相互作用改变了其电子能带结构。结果,打开了约200 meV的能隙,这可以很好地解释观察到的半导体等离子体激元行为。特别是, 当费米能级位于半导体塌缩碳纳米管的带隙中时,在V g = 0 V 时观察到的低光学响应是由于自由载流子湖造成的。此外,其他转变,例如从半导体到金属的转变,也预计会在结构塌陷中发生,这在很大程度上取决于CNT 的手性。相应地,碳纳米管的光学和电子特性可以通过 vdW 封装进行结构调整。
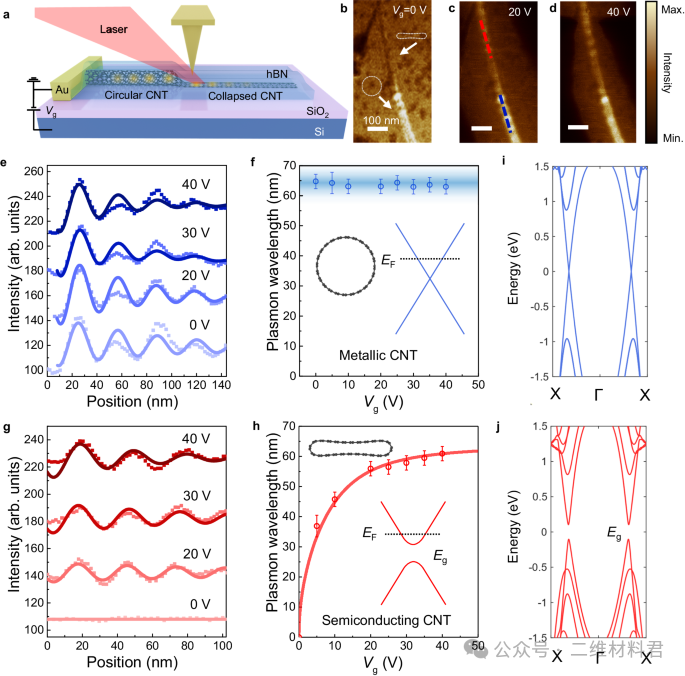
图 4:结构塌陷引起的金属-半导体转变。a 样品结构图解和扫描近场光学显微镜 (SNOM) 示意图。部分 CNT 由于 vdW 压力而塌陷,并在圆形和塌陷的 CNT 之间形成结。b – d 0 V、20 V 和 40 V 不同栅极电压下的近场红外图像。比例尺为 100 nm。e提取的圆形金属碳纳米管(蓝点)和g不同栅极电压下塌缩部分(红点)的等离子体轮廓。线条通过指数衰减的正弦曲线进行拟合。f具有不同栅极电压的金属型(蓝点)和h半导体型(红点)的提取等离子体波长。该线由半导体碳纳米管中的非线性卢廷格液体等离子体激元理论拟合。误差线代表多个波长值测量的标准偏差。i计算出的本征金属 CNT 的能带结构,j塌陷的 CNT,显示带隙的开口。
结论
我们已经证明,vdW 封装能够产生几 GPa 的局部高压。这种局部高压会导致碳纳米管塌陷,塌陷率高达约77%。我们的 MD 模拟完全捕捉到了局部高压和塌陷。我们进一步表明,碳纳米管的结构塌陷可以在金属碳纳米管中打开带隙并诱导金属-半导体转变。我们的研究结果提供了一种制备能带隙可调的塌陷碳纳米管的新方法,这有利于其在电子和光电子领域的实际应用。此外,vdW 封装可以作为一种简单的方法来产生几 GPa 的局部高压,用于探索纳米尺度的新型高压现象。
方法
样品制作
通过热蒸发(蒸发速率:0.004 nm s -1,基础真空压力:1 × 10 -6 mbar)将催化纳米颗粒(Fe)沉积在SiO2 /Si芯片上。然后将芯片放入管式炉(安徽贝琪装备技术有限公司)中,在常压氢气和氩气混合气体下逐渐加热至CNT生长温度(850℃)。当达到生长温度时,用甲烷代替氩气以开始CNT生长。60分钟的生长期后,系统在氢气和氩气保护气氛下冷却至室温。之后,将PPC薄膜上机械剥离的hBN薄片转移到SiO2 /Si芯片上生长的CNT上。最后,将封装的 CNT 样品暴露于 280°C 的氢等离子体中,以去除所有有机残留物和污染物。获得的六方氮化硼封装的纳米管密度非常低,通常彼此相距几微米,如补充图 10所示。采用标准电子束光刻、电子束沉积和剥离技术将金电极定位在碳纳米管的独立部分上。
近场红外成像
自制的扫描近场光学显微镜(SNOM)用于等离子体激元的近场红外纳米成像。 CO 2激光束(10.6 μm)聚焦到 SNOM 系统中导电 AFM 尖端的顶点。尖端顶点处的增强光场与尖端下方的 CNT 相互作用。携带 CNT 样品局部光学信息的散射光由放置在远场的 MCT 探测器(KLD-0.1-J1,Kolmar)收集。使用锋利的 AFM 尖端可以获得空间分辨率优于 20 nm 的近场光学图像。在我们的测量过程中,这种近场红外图像与 AFM 形貌扫描同时记录。
拉曼测量
使用商用 Renishaw inVia Qontor 共焦拉曼显微镜进行该测量。 532 nm 波长的激光束通过 100 倍物镜 (NA = 0.9) 聚焦到样品上。激光器的功率约为2 mW。光栅刻槽密度选择为1200刻槽mm -1。
DFT计算
第一原理 DFT 计算是使用维也纳从头算仿真包、投影仪增强波方法和 Perdew-Burke-Ernzerhof 泛函的广义梯度近似来执行的。计算中使用了 1.42 Å 的碳键长度和足够厚 (>10 Å) 的真空层。为了在DFT计算中模拟hBN对CNT施加的外部vdW压力,我们在CNT的两侧固定了两个hBN层,并且仅松弛碳原子的坐标,直到力低于0.01 eV Å -1。两个六方氮化硼层之间的不同固定距离对应于对碳纳米管施加的不同压力。
分子动力学模拟
模拟模型系统由单元碳纳米管(扶手椅式、锯齿形和(22,1)碳纳米管)、大型石墨烯基板和三层顶部石墨烯组成。在模拟过程中,基板保持固定。封装的碳纳米管模型内的层内相互作用是通过 AIREBO 势计算的。 CNT 和石墨烯层之间的层间相互作用通过具有精细参数化的依赖于注册表的 ILP 进行描述,我们在 LAMMPS 中实现了这一点。封装的碳纳米管的初始构型是使用 cg 算法通过几何优化生成的,并在三层石墨烯的边缘添加向下的力 (2 eV Å -1 )。封装的碳纳米管的最终结构以 10 − 6 eV Å − 1的阈值力进行优化。









