扩散模型综述

22年9月 来自北大、北邮和美国加拿大几所大学研究机构 的扩散模型综述“Diffusion Models: A Comprehensive Survey of Methods and Applications“。

摘要 ：扩散模型是一类AI生成深度模型，在各种任务上显示出令人印象深刻的结果，具有坚实的理论基础。尽管扩散模型取得成功，但往往需要昂贵的采样程序和次优的似然估计。已经在改进扩散模型性能上各方面作出了重大努力。本文对扩散模型的现有方法进行全面回顾。具体来说，提供扩散模型的分类法，划为三种类型： 采样加速增强，似然最大化增强和数据泛化增强 。还介绍其他生成模型（即变分自编码器、生成对抗网络、归一化流、自回归模型和基于能量的模型），并讨论扩散模型与这些生成模型之间的联系。然后，回顾扩散模型的应用，包括计算机视觉、自然语言处理、信号处理、多模态建模、分子图生成、时间序列建模和对抗性纯化。此外，提出一些与生成模型开发相关的新观点。

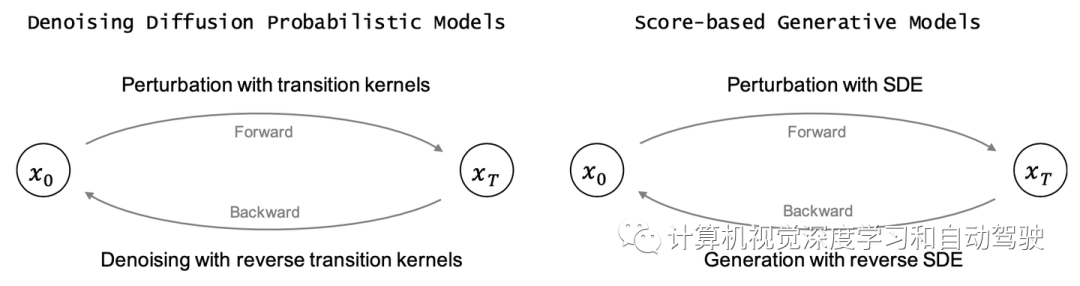
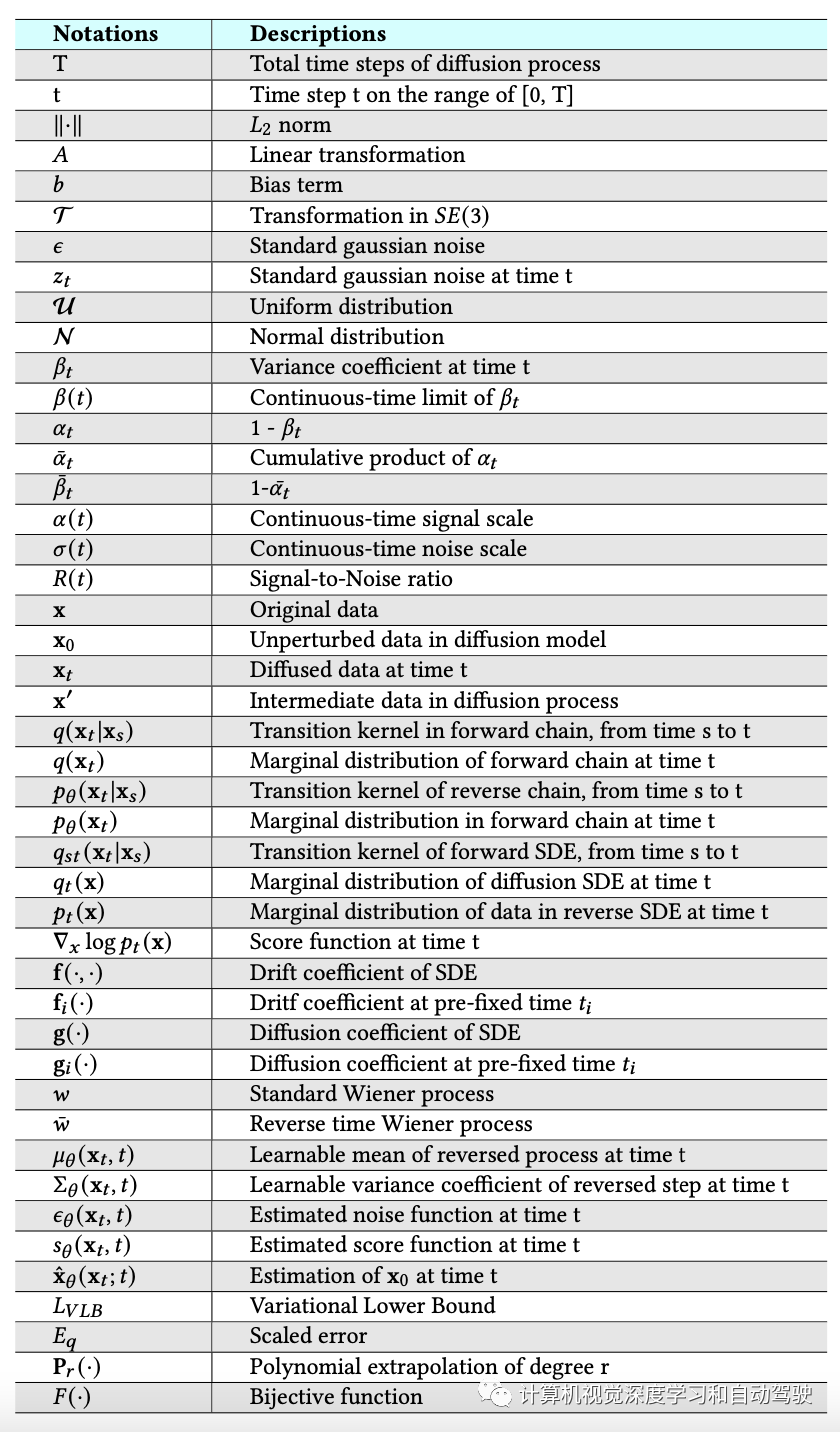
生成建模的一个核心问题是模型概率分布的灵活性和易处理之间的权衡。扩散模型的基本思想是通过正向扩散过程系统地扰动数据分布中的结构，然后通过学习反向扩散过程来恢复结构，从而产生高度灵活和易于处理的生成模型。如图显示了扩散模型中两种主要范式之间的比较，即去噪扩散概率模型和基于分数的生成模型。下表列出了用于描述以下扩散模型的符号。

去噪扩散概率模型（DDPM）[78]由两个参数化的马尔可夫链组成，并使用变分推理在有限时间后生成与原始数据匹配的样本。前向链通过预设计的时间表逐渐添加高斯噪声来扰乱数据分布，直到数据分布收敛到给定的先验，即标准高斯分布。反向链从给定的先验开始，并用参数化的高斯转移核学习逐渐恢复未受干扰的数据结构。

目标函数可以通过蒙特卡罗尔算法[146]估计，并使用随机优化器[196]进行训练。在生成过程中，首先从标准高斯先验中选择一个样本，然后用学习的反向链按顺序描绘出一个样本，直到获得新数据。

或者，可以将上述扩散概率模型视为基于分数生成模型的离散化[195]。基于分数的生成模型构建随机微分方程 （SDE），以平滑的方式干扰已知先验分布的数据分布，以及相应的反向时间 SDE 将先验分布转换回数据分布。

DDPM [78] 中的前向过程可以看作是特殊的前向 SDE 离散化。反向 SDE 的解与前向 SDE 具有相同的边际密度，但它在时间上反向演进。要反向这个扩散过程并生成数据，唯一需要的信息是每个时间步的评分函数（梯度）。借用分数匹配[191]的技术，可以训练一个基于时间依赖的基于分数模型，通过优化去噪分数匹配目标来估计分数函数。

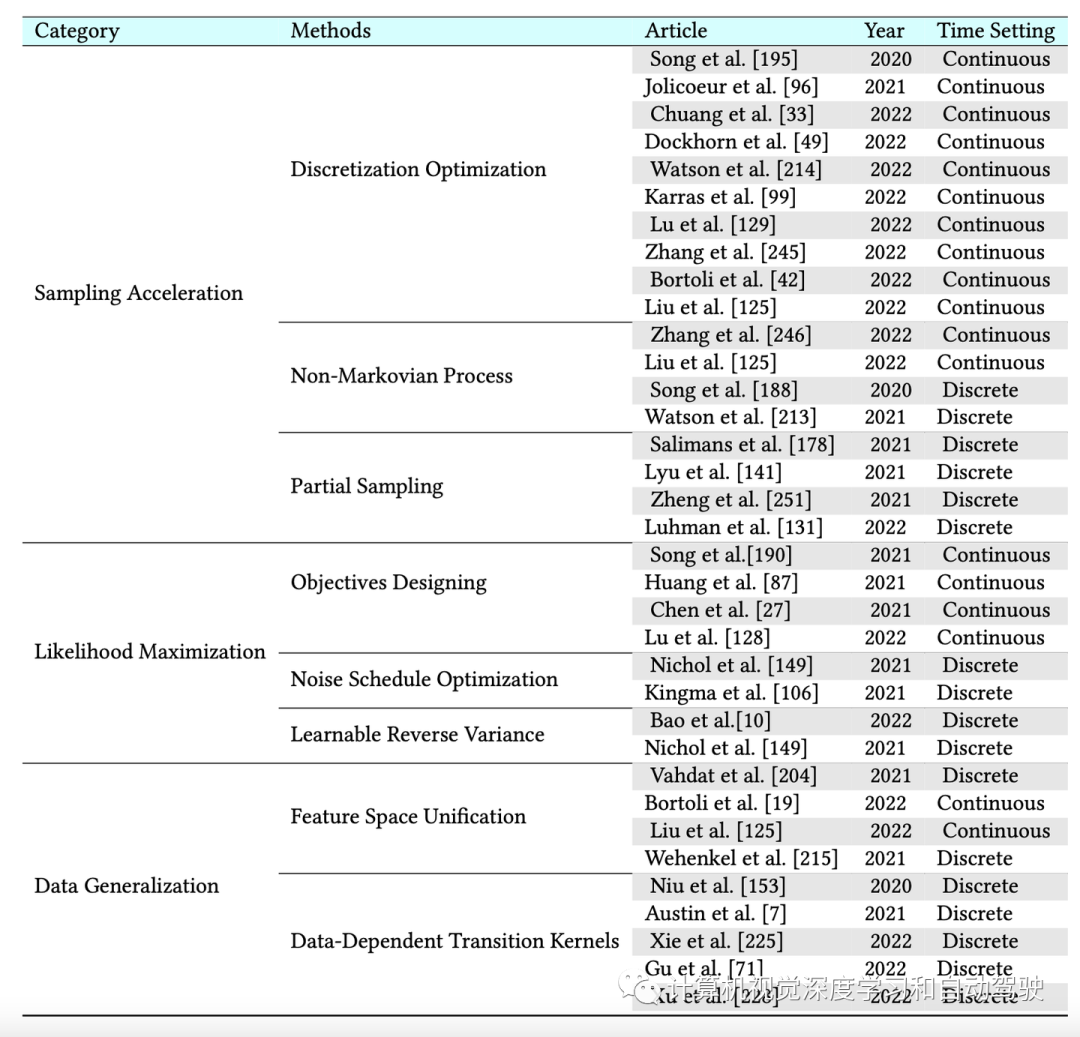
经典扩散模型有三大缺点：采样程序效率低下、似然估计欠佳、数据泛化能力差。近年来，为解决这些缺点作出了重大努力。高级扩散模型分为三类：采样加速、似然最大化和数据泛化，与模型增强有关，如下表给出为例。

马尔可夫过程仅依靠最后一步的样本进行预测，限制了先前大量样本的信息利用。相反，非马尔可夫过程的转换核可以依赖更多的样本，并且可以利用来自这些样本的更多信息。因此，它可以以较大的步长做出准确的预测，从而相应地加快采样过程。DDIM [188] 将原始 DDPM 扩展到非马尔可夫情况。DDIM的生成方案可以看作是ODE（ordinary differential equation）的特殊离散化；因此，可以确定性地对数据进行采样。GGDM [213] 建议在生成过程的每一步使用所有先前的样本来预测下一个样本，这泛化了 DDIM。

生成模型是一个热门的研究领域，具有许多应用。例如，生成高质量图像[100]，合成逼真的语音和音乐[205]，推进半监督学习[38，108]，识别对抗性示例[193]，模仿学习[77]，强化学习优化[156]。如表总结将扩散模型与其他生成模型集成的算法，如图 还提供了示意图。