“你认为最美的数学、物理方程是什么？”当代十位大数学家、物理学家给出了他们自己的回答。这些回答构成了大雅之美（The Concinitas Project）的十篇文章。我们分上下两期，为读者带来这些大师对自己眼中最美方程的精彩解读。在本文中，我们将会看到代数几何学家芒福德（Mumford）、数论家邦别里（Bombieri）和数学物理学家戴森（Dyson）则提出了纯数学中的一些精妙的公式。著名的物理学家、诺贝尔物理学奖得主温伯格（Weinberg）和盖尔曼（Gell-Mann）也各自推出了其成名作。
上期回顾：数学物理学家心中的十大最美方程（上）
撰文 大卫·芒福德1（David Mumford）
翻译 陈见柯（中国传媒大学）
校译 林开亮
数学家们一大部分的工作是在研究那些经推理而得的“对象”，使其变得像我们日常生活一样真实，虽然它们远非实物一样地存在。柏拉图2正多面体在高维情形的推广是相对简单的例子。人们希望能在高迪3主持修建的圣家族大教堂4的某个尖顶上放置正二十面体，这的确是可真实触碰的对象。但数学家们一致认为，空间的维数可以超过3，19世纪数学家施莱夫利5发现了柏拉图多面体在四维情形下的推广。对此，我们只能想象。记Mg是亏格g的光滑射影曲线的模空间，很长时间里，我的一直关注于如何很好地理解其结构。在我的学生时代，即便以数学家所谓清晰的标准来看，这类空间似乎依旧笼罩在烟雾之中，它们是一种介于成熟数学和幻象之间的存在。我一度努力改变这种状况。
与此同时，亚历山大·格罗滕迪克6横空出世。他有着前人从未具有的高度抽象的思维能力，并对人们尚未理解的具体问题予以启发。事实证明，他深刻的结果可以应用于长期困扰我的空间结构问题。而那时的我却不知该如何利用。这些结果的强大之处在20年后才变得明显起来：通过与乔·哈里斯7合作，我们终于能够将Mg看作真实的对象（借助标准术语，它是一个拟射影代数簇）。
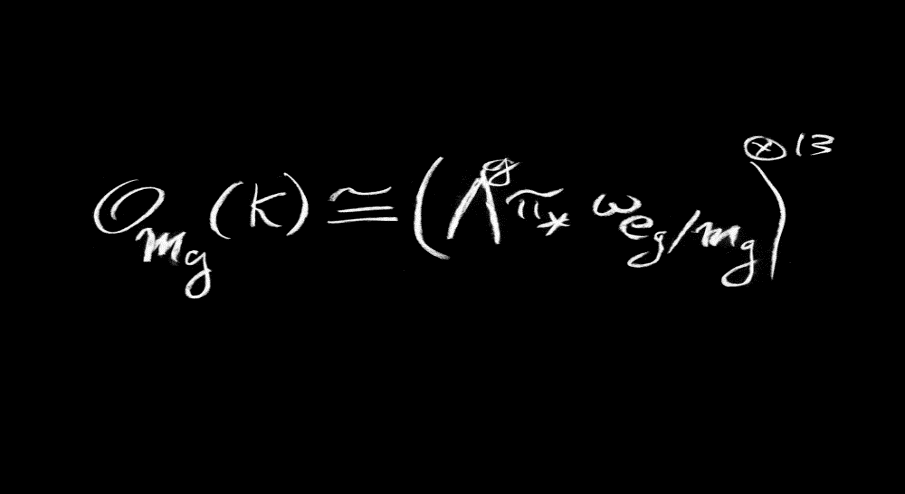
这个公式意味着什么？它优美在何处？它表明：两个对象（“线丛”）本质相同（“同构”）。等式左边的对象决定Mg的几何。追溯至高斯8，人们就已经知道空间可大致分为三种：像平面一样的平坦空间；像球面一样的正曲率空间；以及像马鞍面一样的负曲率空间（曲面上三角形内角和小于180°）。等式左边决定了Mg在上述三分法中的位置；博特9将等式右边称为“重言”结构：完全由Mg决定的基本对象。上述同构表明，在g充分大的条件下，Mg是负曲率空间。
上述公式最让人惊讶的地方是数字13。翻阅数学杂志，你会发现，除页码外，论文中一般不会出现大于2的数字。此处出现的13是计数得出的，计数问题有悠久的历史，另一个著名的例子，是一个三次曲面上恰好有27条直线（包括复直线）。就此而言，我始终觉得造物主在跟我们开玩笑。
1 大卫·芒福德，David Mumford，1937年——，美国数学家。
2 柏拉图，Plato，约公元前427年——公元前347年，古希腊哲学家。
3 安东尼·高迪，Antoni Gaudí，1852年——1926年，西班牙建筑师。
4 圣家族大教堂（加泰罗尼亚语：Basílica i Temple Expiatori de la Sagrada Família），又译作神圣家族大教堂，简称圣家堂（Sagrada Família），是位于西班牙加泰罗尼亚巴塞罗那的一座罗马天主教大型教堂，始建后由西班牙建筑师安东尼·高迪接手设计与建设。
5 路德维希·施莱夫利，Ludwig Schläfli，1814年——1895年，瑞士数学家。
6 亚历山大·格罗滕迪克，Alexander Grothendieck，1928年——2014年，法国数学家。
7 乔·哈里斯：Joe Harris，1951年—— ，美国数学家。
8 卡尔·弗里德里希·高斯：Carl Friedrich Gauss，1777年——1855年，德国数学家。
9 拉乌尔·博特：Raoul Bott，1923年——2005年，匈牙利裔美国数学家。
撰文 邦别里10（Enrico Bombieri）
翻译 林开亮（西北农林科技大学理学院）
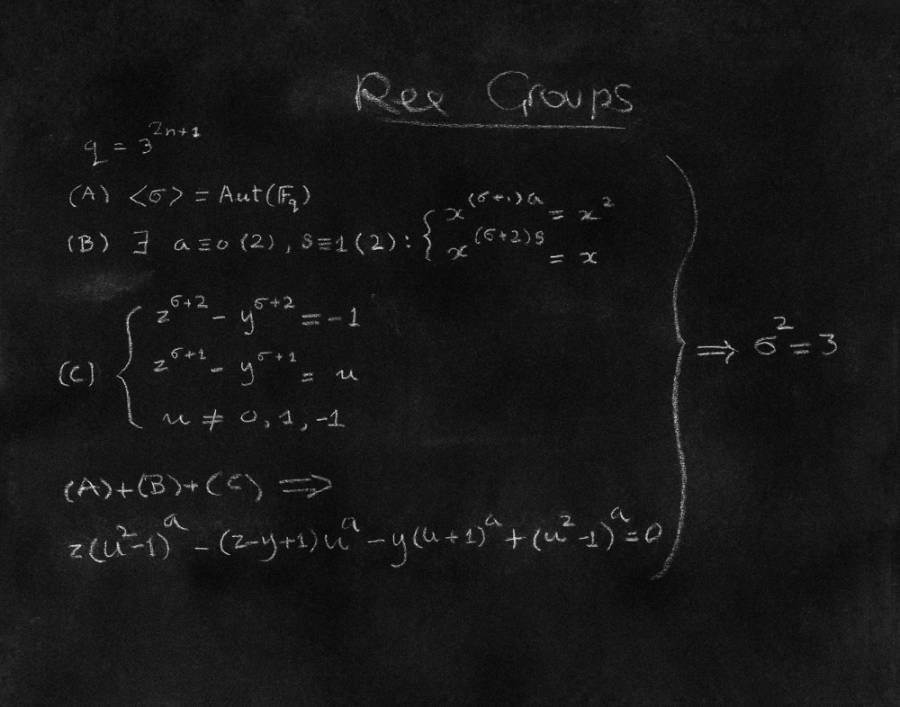
数学中存在美吗？这个问题关心的是数学对象及其关系，可被验证的证明即真正的数学对象。数学家通常会赞同，在定理和证明的结构之中的确存在着美，即便大多数时候这种美只有数学家自己才能看得到。
群的概念漂亮地表达了数学中的对称。群是什么？考虑任意一个对象，不论它是具体的还是抽象的。该对象的一个对称——数学的行话叫自同构——就是该对象到自身的一个保持它的所有性质的映射。两个对称的乘积，即两个映射的复合，仍然是一个对称，而且每个对称都有一个倒过来的逆。数学家认为连续的Lie群——譬如圆周或球面的旋转群——是很大一部分数学和物理的漂亮基础。除了连续的Lie群，还有不连续的有限群和离散群；有一些是通过将Lie群约化到一个有限或离散的框架下得到的。
群可以极其复杂。给定一个群，也许会出现这样的情况，存在从该群到另一个群的一个保持乘积结构的映射。一个群称为单群，如果这样一个映射的像要么是该群的一个复本要么是只有一个元素（恒同映射）的平凡群。单群是构建所有群的基本积木，因此在研究任意群时，知道所有的单群非常重要。对称的一般有限群首次出现在伽罗瓦（Évariste Galois）关于代数方程的工作中。伽罗瓦在18岁时就证明了五次一般代数方程不可通过代数操作求解，其论证要点是，作用在5个字母a,b,c,d,e上的偶置换（即由偶数个对换相乘得到的置换）群A5是单群。这个群是最小的非交换的单群，同时也是正二十面体的对称群。正二十面体是一个非常漂亮的几何对象！可以想见，单群可以描述为一些特殊几何对象的对称群。然而，研究一个抽象化、假设出的单群，其困难恰恰包含了从其内蕴性质构造出一个丰富的几何对象。迄今为止，罗列出所有有限单群的分类定理的完全证明占据3000多页篇幅，汇聚了一百多位数学家近四十年的努力。
源自Lie群的有限单群系列很容易就发现了，只有三个例外。这些系列不是来自实数或复数，而是来自特征为p的有限域，这里p是一个素数。在特征为p的有限域里，仍然可以做普通的算术，不过，一个数用p去乘总是得到0。一切都很顺利，即便可能没那么容易，除了数学家Ree的发现——特征2下的Lie群B2和F4和特征3下的G2也存在额外的对称，它们可以得到新的单群系列，今天我们称之为twisted Ree 群——留下的问题：twisted B2群及其唯一性之前由铃木（Suzuki）通过完全不同的方法得到，F4情形的唯一性也得到了，但G2情形则难以捉摸。
经过汤普森（Thompson）的艰苦努力，G2的唯一性问题归结为，证明特征为3的有限域上的某个满足一组极其复杂的多元方程组的变换σ，具有性质其平方σ2作用于x如同x3，换言之σ2=3。不幸的是，消元法的普通代数操作很快就会给出项数是如此之多的等式，以至于全世界所有的计算机合在一起都无法存储下来。怎么办？早在1973年，汤普森就引发了我对这个问题的兴趣，但我迷失在公式的迷宫里。1979年，当有限单群的分类工作达到高潮时，我再一次考察了汤普森等式。我自问：是否有必要写下这些“不可能”的公式，也许有办法可以绕开。利用一个奇妙的技巧，可以发现，通过消元能够提取到一点点有用的额外信息，再度利用那一技巧重新消元并结合新的信息，额外的信息可以精细化。重复这个精细化过程三次，就得到了所需要的等式σ2=3，除了极少数情形需要用计算机验证。因此，唯一性的问题解决了，另一项技巧也添加到有限单群分类的证明中。11
这个等式是用白色粉笔写在暗蓝灰色的黑板上，左边是汤普森等式，双箭头指向σ2=3，意指左边的等式蕴含了twisted Ree群的唯一性。问题很漂亮，而所期待的解答也很简单，因而优美，汤普森等式具有内在隐秘的美，因为它反映了一个群的性质。对专家来说，避开蛮力而得到的解答也具有其自身的美。事实上，数学家在追寻其真理时——有时是自动地——以寻求美为向导。正如诗人济慈（Keats）所说，美即真，真即美。
10 谢谢Sarah Jones Nelson。
11 Bombieri, Enrico. "Thompson's Problem (σ2=3).." Inventiones mathematicae 58 (1980): 77-100.
撰文 戴森（Freeman Dyson）
翻译 林开亮（西北农林科技大学理学院）
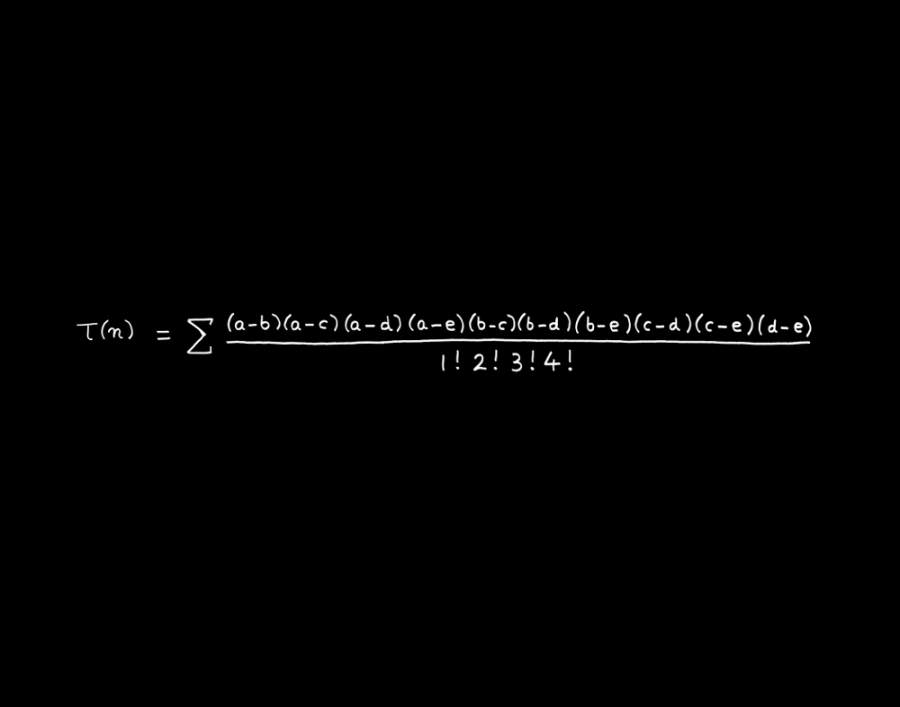
麦克当纳（MacDonald）等式是我最美妙的发现。它属于数论，这是数学中最无用和最古老的分支。我的朋友麦克当纳（Ian MacDonald）享受了第一个发现它的快乐，而我作为第二个发现者享有几乎同等程度的快乐。我们的女儿在同一班上小学，因此我们谈论我们的女儿而不谈数学。我们发现了τ函数满足的一个方程，τ函数是32岁英年早逝的印度天才数学家拉马努金（Srinivassa Ramanujan）最后四年里探究的课题。这里我写下τ函数的麦克当纳等式。
麦克当纳等式具有神奇的五重对称性，这一点逃过了拉马努金的法眼。在等式的右边，有十个乘在一起的差，此即五重对称性。我们要感激拉马努金，不仅感激他所发现的许多美妙的东西，还有他留给后人发现的其它美妙的东西。
为解释麦克当纳等式的意义，我们来查考一下最简单的三种情况，n=1,2,3求和取遍所有满足条件a+b+c+d+e= 0且a2+b2+c2+d2+e2=10n的整数a,b,c,d,e。而“(mod5)”的条件意味着，a是被5除余1的数，b是被5除余2的数，c是被5除余3数，d是被5除余4的数，e是被5除余0（整除）的数。而等式中的惊叹号含义是1!=1,2!=1×2=2,3!=1×2×3=6,4!=1×2×3×4=24。因此，当n=1时，a,b,c,d,e只有唯一取值1,2,-2,-1,0，根据MacDonald等式，我们得到τ(1)=1。当n=2时，a,b,c,d,e只有唯一取值1,-3,3,-1,0，我们得到τ(1)=-24。当n=3时，a,b,c,d,e有两种取值1,-3,-2,4,0和-4,2,3,-1,0，我们得到τ(3)=252。容易验证，τ(n)的这三个值与Ramanujan等式给出的值一致。
麦克当纳等式是麦克当纳发现的存在于两种对称之间的更深刻联系的一个特殊情况。这两种对称我们分别称为模对称与仿射对称，它们最初在科学的不同部分被发现，模对称来自数学，仿射对称来自物理。每个人都可以通过欣赏艺术埃舍尔（Mauritz Escher）画中飞翔的天使与魔鬼而看到模对称的展示。埃舍尔懂得数学，准确掌握了细节。仿射对称则体现于物理学家用高能加速器创造的粒子的稀有组合中。数学家朗兰兹（Robert Langlands）第一个猜测出这些对称与其它类型的对称之间的联系。麦克当纳在实现朗兰兹的梦想方向上迈出了一大步。我在这里所写下的等式仅仅是麦克当纳那一大步留下的一点印记。
撰文 温伯格（Steven Weinberg）
翻译 刘云朋（天津大学理学院）
校译 林开亮
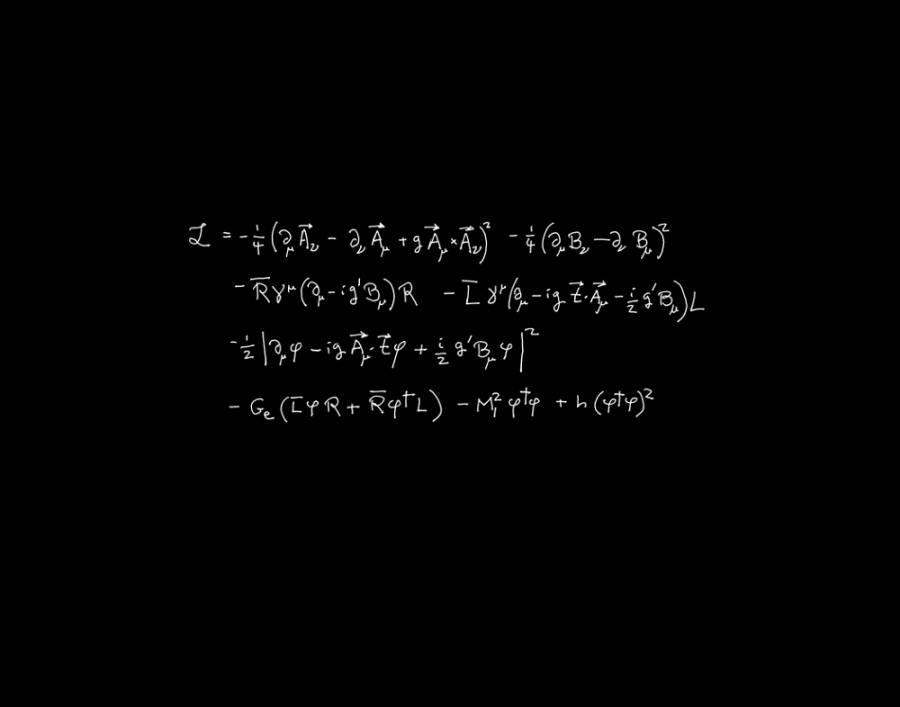
这是方程的原始版本，后来成了自然界两种基本的力——电磁力与弱核力——的标准理论。弱核力尽管不像电磁力那么常见，却产生一种重要的放射性（β衰变）以及核反应链的第一步（太阳和其它恒星赖此发热）。我在这方面的第一篇论文发表于1967年，其中的(4)式就是这个方程。它在那几年是基本粒子物理领域发表的论文中引用最多的，也许现在仍然如此。
电弱理论是一种场论，它的基本成分是场，其中也包括电场和磁场。方程左侧的L由场及场的变化率组合而成，称为此理论的拉格朗日密度。拉格朗日密度是像能量密度那样的东西，根据物理学家从二十世纪三十年代就开始使用的规则，理论中各种场所遵循的方程都方便地蕴含在拉格朗日密度之中。
方程右边的大部分符号是理论中的各种场。弱力和电磁力由
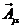和
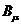传递，电场和磁场是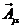和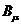的组合。中微子和左手电子场（该场描述的电子，其自旋对运动方向的环绕与左手四指弯曲时对拇指的环绕方向一致）合在一起用L表示。右手的电子场用R表示。g 和 g’是数值常数，与电子的荷有关，其值只能从实验得到。
符号φ 表示某四分量的场，它与其它场相互作用，从而赋予电子质量而使中微子仍无质量，赋予传递弱相互作用的三种粒子质量而使光子（光的粒子）仍无质量。余下的常数Ge、M12、h 与电子的质量、弱力的强度有关。φ 场的四分量之一对应某种新的粒子，到2012年实验上才见到它的踪影。方程的第三、四行描述了理论中中微子和左手电子之间、弱力和电磁力之间的对称性破缺机制。
这个方程可能看似不大美，它美在浑然天成——给定成分后，其结构可由数学的自洽条件很好地确定下来。略去一行，甚或只把一个负号改成正号，都会让整体不再自洽。
方程从简，略去了缪子（一种像电子而更重的粒子）和相应的中微子。显然，可以类比电子及其中微子把它们包含进来。
1971年，此理论进而把夸克（构成质子和中子的基本粒子）也包含进来，之后不断得到实验的验证。
撰文 盖尔曼（Murray Gell-Mann）
翻译 刘云朋（天津大学理学院）
校译 林开亮
1932年发现中子，人们开始认识到原子核由中子和质子构成。再向它们内部看去，可以发现每个中子和质子都由三个夸克构成——粗略地说，每种“色”一个
。正是色力把夸克束缚在一起，形成中子和质子。作为变量，色有三个不同的取值，俗称“红”、“绿”、“蓝”。带“色”的物质受到禁闭，无法彼此脱离而单独探测。在三种色互相转换的色SU3 变换群下，物理理论完美地对称。
这里的表达式给出“量子色动力学(QCD)”的拉格朗日密度，它用数学表达式概括了强相互作用的动力学。强相互作用同引力、弱力、电磁力一样，都是自然界中基本的力。此表达式美在寓真实于其中。它还美在简洁，不过是做了一点清理之后的简洁。这里有三项，前两项Lgt、Lq 分别包含胶子、夸克的贡献（场），Laddl 包含“附加”项，其中部分的场最终预言了近期才发现的希格斯玻色子。
追忆往昔，我与诸同事获得这个公式，并非灵光乍现，而是厚积薄发。这公式不仅总结了大自然的一个真理，还凝聚着日积月累的大量艰苦工作。它的每一项都荟萃了数年研究发现的精华。随着时间推移，我和其他人清楚了要把哪些项包含其中。（我想补充一点，我们在以有点与众不同的方式考虑强相互作用。）我们本可以在中间任何一步停下来，把更多的东西丢给“附加”项，但这个公式感觉很好，它很完整，满足SU3 群所要求的对称性条件。这条件也让我们无法涉足当时尚未完全探索的领域。所以，它尽管真实，在某种意义下却并非终极真理，总有更多的细节可以补充进去——除了希格斯，还有多种标量场，我们知道其存在，却不清楚如何正确描述——从而有更多的东西尚待发现，这也是一种美。
本文译自：
http://www.concinnitasproject.org/portfolio/
本文原载《中国数学会通讯》2017年第1期，经再次修订编辑后发表在“环球科学”微信公众号。感谢《中国数学会通讯》授权刊登。
大雅之美由“数学火炬手”中的部分成员翻译。“数学火炬手”是一群热爱数学的中青年数学爱好者，大部分是活跃于各个高校的数学教师和物理教师，致力于与公众分享美妙的数学，推动数学的普及。就像奥运火炬手一样，数学火炬手期待成为数学普及的领跑者，促进公众对数学的认识。本项目是“数学火炬手”合作完成的第一个项目，以后会推出更多精彩的作品。
——数学火炬手代表 林开亮（西北农林科技大学理学院数学教师）
