大家经常看到的贝叶斯公式（Bayes）是写成如下图的形式，通常以P(A|B)，P(B|A)的形式表示，虽然数学上看着简单，那到底A，B是什么意思，应该怎么去理解呢，然后怎么运用于实际情况呢？
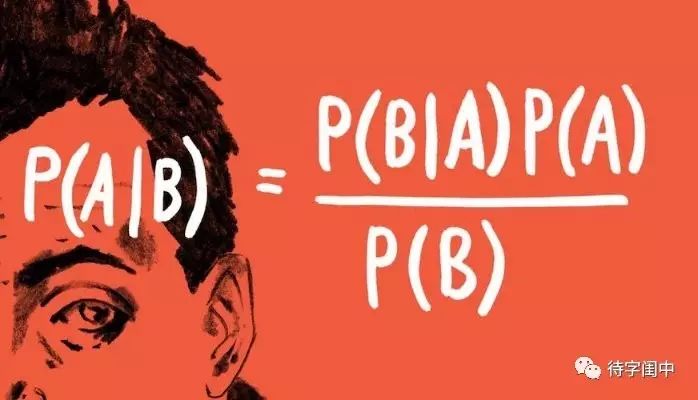
贝叶斯（Bayes）公式是解决由观察到的现象（或是测量的数据）去推断现象（或是数据）后面的规律（或是假设）的发生的概率的问题。那么如果将上面公式中的A换成“规律”，B换成“现象”，这个公式就一目了然，能很容易理解和运用了。
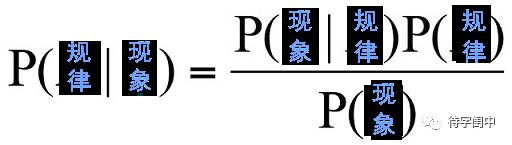
对于一个场景，可能有几种不同的规律来解释，根据对场景的一些现象的观测，怎么知道各种可能的规律在背后发生作用的概率，这就是想回答的问题P(规律|现象)。直接去计算有难度，但是我们知道在某个规律下，不同现象发生的概率P(现象|规律)，和每个现象发生的概率P(规律)，和不同现象发生的概率P(现象)。贝叶斯就是告诉怎么用这些知道的知识去计算现象后面的规律发生的概率（具体推导请参考条件概率和文氏族图）。所以，最重要的是分清（理解）场景或是问题中的规律和现象！
看几个例子。
第一个例子。两个一模一样的碗，一号碗有30颗水果糖和10颗巧克力糖，二号碗有水果糖和巧克力糖各20颗。现在随机选择一个碗，从中摸出一颗糖，发现是水果糖。请问这颗水果糖来自一号碗的概率有多大？
分清和定义现象和规律。这儿有两个规律：从一号碗来规律，从二号碗来规律。有两种现象：水果糖现象，巧克力现象。而且知道两个一模一样的碗，所以两个规律的概率一样，P(从一号碗来规律)＝P(从二号碗来规律)＝0.5。同时知道P(水果糖现象|从一号碗来规律)＝30/(30+10)=0.75，P(巧克力现象|从一号碗来规律)=10/(30+10)=0.25；P(水果糖现象|从二号碗来规律)=20/(20+20)=0.5，P(巧克力现象|从二号碗来规律)=20/(20+20)=0.5。另外，P(水果糖现象)＝(30+20)/(30+10+20+20)=0.625，P(巧克力现象)=(10+20)/(30+10+20+20)=0.375。现在的问题是观察到了一个水果糖现象，要求推断后面的规律，即从一号碗来的规律的概率是多大，也就是P(从一号碗来规律|水果糖现象)。
好了，有了前面那些知识，根据贝叶斯公式，就可以计算问题的答案。
P(从一号碗来规律|水果糖现象)＝P(水果糖现象|从一号碗来规律)*P(从一号碗来规律)/P(水果糖现象)=0.75*0.5/0.625=0.6。
这样，理解了问题中的现象和规律，是不是就很好理解了。
第二个例子。一所学校里面有 60% 的男生，40% 的女生。男生总是穿长裤，女生则一半穿长裤一半穿裙子。假设你走在校园中，迎面走来一个穿长裤的学生（很不幸的是你高度近似，你只看得见他（她）穿的是否长裤，而无法确定他（她）的性别），你能够推断出他（她）是男生的概率是多大吗？
同样，分清和理解问题中的规律和现象。这儿有两个规律：是男生规律，是女生规律。而且知道各个规律的发生概率P(是男生规律)=0.6，P(是女生规律)=0.4。有两种现象：穿长裤现象，穿裙子现象。而且知道各个现象发生概率，假设有10个学生，6个男生，4个女生，那么，P(穿长裤现象)=(6+2)/10=0.8，P(穿裙子现象)＝2/10=0.2。另外，P(穿长裤现象|是男生规律)=1.0，P(穿裙子现象|是男生规律)=0.0，P(穿长裤现象|是女生规律)=0.5，P(穿裙子现象|是女生规律)=0.5。现在，看到了一个穿长裤的学生，需要推断是男生的概率，即P(是男生规律|穿长裤现象)。
好了，有了前面那些知识，根据贝叶斯公式，就可以计算问题的答案。
P(是男生规律|穿长裤现象)=P(穿长裤现象|是男生规律)*P(是男生规律)/P(穿长裤现象)=1.0*0.6/0.8=0.75。
再次看到，只要理解了问题中的规律和现象，运用贝叶斯公式是多么自然和容易。
所以，理解和运用贝叶斯公式的关键是：理清问题中的规律和现象！
思考题：
垃圾邮件检测中，什么是规律，什么是现象？
拼写错误纠正中，什么是规律，什么是现象？
