用遗传算法实现符号回归或可运用到大气污染臭氧预报领域——浅析gplearn

第一时间获取气象科研资讯

『 气象学家 』 公众号 交流群

加入

提起Python里的机器学习包，我们通常会想到Scikit-Learn、XGBoost、LightGBM、Keras和TensorFlow。在这里，我将向大家介绍gplearn。它是目前Python内最成熟的符号回归算法实现。

原文链接可见：https://zhuanlan.zhihu.com/p/31185882

（摘自知乎作者光喻）

简介

在线性模型中，目标变量y可以表示为：

然而，即使加入了多项式特征，它也很难发现特征变量与目标变量之间更复杂的关系。

作为一种一种监督学习方法， 符号回归 （ symbolic regression ）试图发现某种隐藏的数学公式，以此利用特征变量预测目标变量。

符号回归的具体实现方式是 遗传算法 （ genetic algorithm ）。一开始，一群天真而未经历选择的公式会被随机生成。此后的每一代中，最「合适」的公式们将被选中。随着迭代次数的增长，它们不断繁殖、变异、进化，从而不断逼近数据分布的真相。
公式的表示方法

假设我们有特征X0和X1，需要预测目标y。一个可能的公式是：

它也可以写作：

同时，我们也可以把它转化成一个S-表达式：

公式里包括了变量（X0和X1）、函数（加、减、乘）和常数（3和0.5）。 有了S-表达式，我们可以把公式表示为一个 二叉树 ：

在这个二叉树里，所有的 叶节点都是变量或者常数 ， 内部的节点则是函数 ；公式的输出值可以用递归的方法求得。

在用遗传算法实现符号回归时，所有的公式都会以S-表达式和二叉树的形式存在。 值得注意的是，上图树内的 任意子树都可以被修改或替代 。 例如，如果把

中的（✖3X1）替换成（✖6X0）,那么我们就得到了一个新的公式：

gplearn包括了一系列不同的函数，以供用户选择。 它们的关键词是：

'add'： 加法，二元运算
'sub'： 减法，二元运算
'mul'： 乘法，二元运算
'div'： 除法，二元运算
'sqrt'： 平方根，一元运算
'log'： 对数，一元运算
'abs'： 绝对值，一元运算
'neg'： 相反数，一元运算
'inv'： 倒数，一元运算
'max'： 最大值，二元运算
'min'： 最小值，二元运算
' sin'： 正弦（弧度），一元运算
'cos'： 余弦（弧度），一元运算
'tan'： 正切（弧度），一元运算

因为输入值很可能是随机产生的，所以这些函数需要处理诸如「除以零」的问题。 因此，gplearn中的许多函数并不符合它们原本的数学定义，而是「受保护」的修改版：

gplearn还允许用户自定义函数。

公式的适应度

物竞天择，适者生存。 ——《天演论》

和其他机器学习算法一样，遗传算法的核心在于衡量公式的 适应度 （fitness function）。 在符号回归里，适应度的地位类似于目标函数、score、loss和error。

gplearn的主要组成部分有两个： SymbolicRegressor 和 SymbolicTransformer 。 两者的适应度有所不同。

SymbolicRegressor是回归器。 它利用遗传算法得到的公式，直接预测目标变量的值。

SymbolicTransformer是转换器。 它并不直接预测目标变量，而是转化原有的特征、输出新的特征，这在特征工程的阶段尤为有效。

SymbolicRegressor的适应度有三种，都是机器学习里常见的error function： mae : mean absolute error

mse : mean squared error

rmse : root mean squared error

SymbolicTransformer会最大化输出的新特征与目标变量之间的 相关系数的绝对值 ： （并非相关系数本身，因为很大的负相关反而有利于预测）

pearson ：皮尔逊积矩相关系数（Pearson product-moment correlation coefficient），默认设置。因为它衡量线性相关度，所以适用于下一个预测器（分类或回归）是线性模型的情况。

spearman ：斯皮尔曼等级相关系数（Spearman's rank correlation coefficient）。因为它衡量单调相关度，所以适用于下一个预测器（分类或回归）是决策树类模型的情况。

当然，用户也可以自定义适应度的标准。

遗传算法内，耗时最大的部分无疑是适应度的计算。所以，gplearn允许用户通过修改 n_jobs 参数控制并行运算。 在数据量和公式数量较大时，并行计算的速度优势最为明显。

公式的进化

gplearn中最重要的超参数都与公式的进化方式有关。

在 初始化 阶段， population_size 棵公式树（参见上文「公式的表达方法」）会被随机生成。 每棵公式树的深度都会受到 init_depth 参数的限制。 init_depth是一个二元组(min_depth, max_depth)，树的初始深度将处在[min_depth, max_depth]的区间内（包含端点）。

通常而言，变量越多，模型越复杂，那么population_size就越大越好。

每棵公式树的初始化方式由 init_method 控制，分为三种策略：

grow ：公式树从根节点开始生长。在每一个子节点，gplearn会从所有常数、变量和函数中随机选取一个元素。如果它是常数或者变量，那么这个节点会停止生长，成为一个叶节点。如果它是函数，那么它的两个子节点将继续生长。用grow策略生长得到的公式树往往不对称，而且普遍会比用户设置的最大深度浅一些；在变量的数量远大于函数的数量时，这种情况更明显。

full ：除了最后一层外，其他所有层的所有节点都是内部节点——它们都只是随机选择的函数，而不是变量或者常数。最后一层的叶节点则是随机选择的变量和常数。用full策略得到的公式树必然是perfect binary tree。

half and half ：一半的公式树用grow策略生成，另一半用full策略生成。因为种群的多样性有利于生存，所以这是init_method参数的默认值。

为了模拟自然选择的过程，大部分「不适应环境」，即适应度不足的公式会被淘汰。从每一代的所有公式中， tournament_size 个公式会被随机选中，其中适应度最高的公式将被认定为生存竞争的胜利者，进入下一代。 tournament_size的大小与进化论中的 选择压力 息息相关： tournament_size越小，选择压力越大，算法收敛的速度可能更快，但也有可能错过一些隐藏的优秀公式。

进入下一代的优胜者未必原封不动——完全不改变优胜者，直接让它进入下一代的策略被称为 繁殖（reproduction） 。 用户可以采取一系列的变异措施：

交叉（Crossover）

优胜者内随机选择一个子树，替换为另一棵公式树的随机子树。此处的另一棵公式树通常是剩余公式树中适应度最高的。

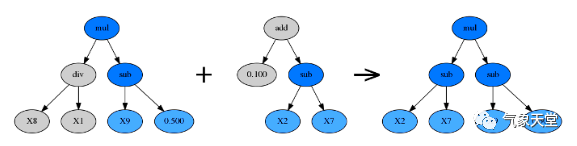子树变异（Subtree Mutation）

由 p_subtree_mutation 参数控制。 这是一种更激进的变异策略： 优胜者的一棵子树将被另一棵完全随机的全新子树代替。

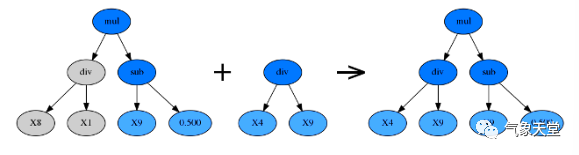hoist变异（Hoist Mutation）

由 p_hoist_mutation 参数控制。hoist变异是一种对抗公式树 膨胀 （ bloating ，即过于复杂）的方法：从优胜者公式树内随机选择一个子树A，再从A里随机选择一个子树B，然后把B提升到A原来的位置，用B替代A。hoist的含义即「升高、提起」。

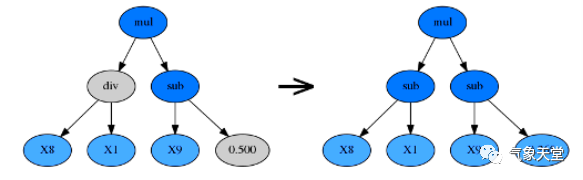
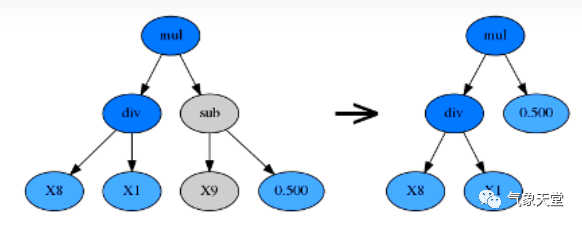点变异（Point Mutation）

由 p_point_replace 参数控制。 一个随机的节点将会被改变，比如加法可以被替换成除法，变量X0可以被替换成常数-2.5。 点变异可以重新加入一些先前被淘汰的函数和变量，从而促进公式的多样性。

由于进化过程的黑箱属性，调参很大程度上依赖于用户的直觉和经验。对于实际问题本身的理解也必不可少，如：最终的公式可能有多复杂？

在使用SymbolicRegressor时，对目标变量进行 标准化 （standardization）和 区间缩放 （min-max-scaling）可以有效避免常数值区间不符的问题。 （假如目标变量的区间是[-1000, 4000]，那么区间为[-1, 1]的常数恐怕不会有多大帮助，最终得出的公式只会是一串几乎毫无意义的加法和乘法。 ）

公式树的膨胀以及解决办法

一棵公式树的复杂度有两个方面： 深度 （树的深度）和 长度 （节点的总数量）。 当公式变得越来越复杂，计算速度也越发缓慢，但它的适应度却毫无提升时，我们称这种现象为 膨胀（bloating） 。

对抗膨胀的方法如下：

1、在适应度函数中加入节俭系数（parsimony coefficient），由参数parsimony_coefficient控制，惩罚过于复杂的公式。节俭系数往往由实践验证决定。如果过于吝啬（节俭系数太大），那么所有的公式树都会缩小到只剩一个变量或常数；如果过于慷慨（节俭系数太小），公式树将严重膨胀。不过，gplearn已经提供了'auto'的选项，能自动控制节俭项的大小。

2、使用hoist变异，削减过大的公式树。

3、每一代的进化中，只有一部分样本会被随机选取，用于衡量公式的适应度。此处样本的数量由参数max_samples控制。这种做法不仅提升了运算速度、保证了公式的多样性，还允许用户查看每一个公式的out-of-bag fitness，更为客观。

例： 符号回归 vs. 决策树 vs. 随机森林

首先，创造一个基于

的数据生成分布：

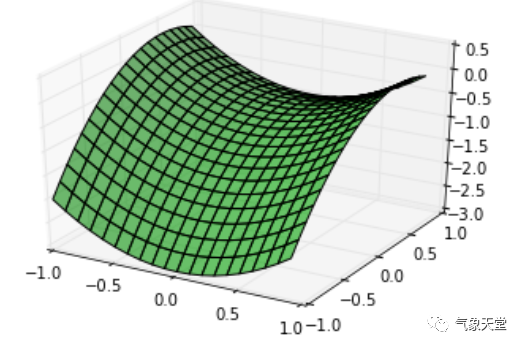
x0 = np.arange(-1, 1, 1/10.)x1 = np.arange(-1, 1, 1/10.)x0, x1 = np.meshgrid(x0, x1)y_truth = x0**2 - x1**2 + x1 - 1
ax = plt.figure().gca(projection='3d')ax.set_xlim(-1, 1)ax.set_ylim(-1, 1)surf = ax.plot_surface(x0, x1, y_truth, rstride=1, cstride=1,                       color='green', alpha=0.5)plt.show()

得出的图象为：

然后，根据数据生成分布生成随机的训练集和测试集：

rng = check_random_state(0)
# Training samplesX_train = rng.uniform(-1, 1, 100).reshape(50, 2)y_train = X_train[:, 0]**2 - X_train[:, 1]**2 + X_train[:, 1] - 1
# Testing samplesX_test = rng.uniform(-1, 1, 100).reshape(50, 2)y_test = X_test[:, 0]**2 - X_test[:, 1]**2 + X_test[:, 1] - 1

接下来，我们训练一个SymbolicRegressor：

est_gp = SymbolicRegressor(population_size=5000,                           generations=20, stopping_criteria=0.01,                           p_crossover=0.7, p_subtree_mutation=0.1,                           p_hoist_mutation=0.05, p_point_mutation=0.1,                           max_samples=0.9, verbose=1,                           parsimony_coefficient=0.01, random_state=0)est_gp.fit(X_train, y_train)
    |    Population Average   |             Best Individual              |---- ------------------------- ------------------------------------------ ---------- Gen   Length          Fitness   Length          Fitness      OOB Fitness  Time Left   0    38.13     386.19117972        7   0.331580808730   0.470286152255     55.15s   1     9.91    1.66832489614        5   0.335361761359   0.488347149514      1.25m   2     7.76      1.888657267        7   0.260765934398   0.565517599814      1.45m   3     5.37    1.00018638338       17   0.223753461954   0.274920433701      1.42m   4     4.69   0.878161643513       17   0.145095322600   0.158359554221      1.35m   5      6.1    0.91987274474       11   0.043612562970   0.043612562970      1.31m   6     7.18    1.09868887802       11   0.043612562970   0.043612562970      1.23m   7     7.65    1.96650325011       11   0.043612562970   0.043612562970      1.18m   8     8.02    1.02643443398       11   0.043612562970   0.043612562970      1.08m   9     9.07    1.22732144371       11   0.000781474035  0.0007814740353     59.43s

作为 比较，我们同时使用scikit-learn的决策树和随机森林进行训练：

est_tree = DecisionTreeRegressor()est_tree.fit(X_train, y_train)est_rf = RandomForestRegressor()est_rf.fit(X_train, y_train)
y_gp = est_gp.predict(np.c_[x0.ravel(), x1.ravel()]).reshape(x0.shape)score_gp = est_gp.score(X_test, y_test)y_tree = est_tree.predict(np.c_[x0.ravel(), x1.ravel()]).reshape(x0.shape)score_tree = est_tree.score(X_test, y_test)y_rf = est_rf.predict(np.c_[x0.ravel(), x1.ravel()]).reshape(x0.shape)score_rf = est_rf.score(X_test, y_test)
fig = plt.figure(figsize=(12, 10))
for i, (y, score, title) in enumerate([(y_truth, None, "Ground Truth"),                                       (y_gp, score_gp, "SymbolicRegressor"),                                       (y_tree, score_tree, "DecisionTreeRegressor"),                                       (y_rf, score_rf, "RandomForestRegressor")]):
    ax = fig.add_subplot(2, 2, i+1, projection='3d')    ax.set_xlim(-1, 1)    ax.set_ylim(-1, 1)    surf = ax.plot_surface(x0, x1, y, rstride=1, cstride=1, color='green', alpha=0.5)    points = ax.scatter(X_train[:, 0], X_train[:, 1], y_train)    if score is not None:        score = ax.text(-.7, 1, .2, "$R^2 =\/ %.6f$" % score, 'x', fontsize=14)    plt.title(title)plt.show()

作图的结果如下：

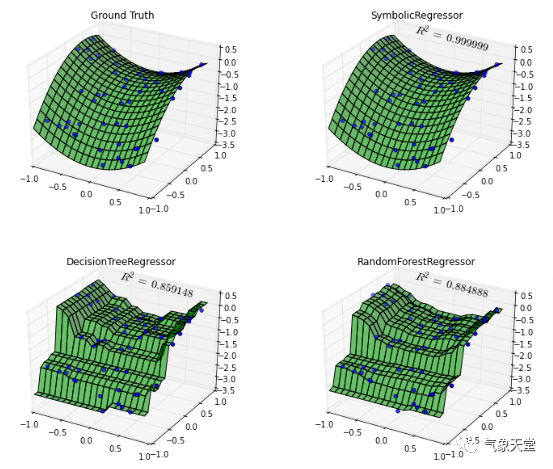如图所示，SymbolicRegressor几乎完美地还原了数据生成分布。