聚类是一种无监督学习(无监督学习是指事先并不知道要寻找的内容,没有固定的目标变量)的算法,它将相似的一批对象划归到一个簇,簇里面的对象越相似,聚类的效果越好。聚类的目标是在保持簇数目不变的情况下提高簇的质量。给定一个 m 个对象的集合。把这 m 个对象划分到 K 个区域,每个对象只属于一个区域。所遵守的一般准则是:同一个簇的对象尽可能的相互接近或者相关,而不同簇的对象尽可能的区分开。之前在文章聚类算法(一)中已经介绍过 KMeans 算法与 bisecting KMeans 算法,本文将会介绍一个流式的聚类算法。
流式聚类算法(One Pass Cluster Algorithm)
既然是流式的聚类算法,那么每个数据只能够进行一次聚类的操作。有一个简单的思路就是对于每一个未知的新样本,如果它与某个类足够相似,那么就把这个未知的新样本加入这个类;否则就自成为一个新的类。如下图所示:
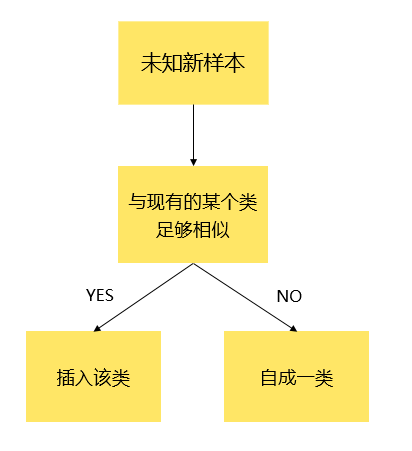
基于以上思路,我们可以设计一个流式的聚类算法。假设 dataMat 是一个 m 行 n 列的一个矩阵,每一行代表一个向量,n 代表向量的维度。i.e. 在 n 维欧几里德空间里面有 m 个点需要进行聚类。
流式聚类的算法细节:
参数的设定:
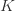 表示在聚类的过程中允许形成的簇的最大个数;
表示在聚类的过程中允许形成的簇的最大个数;
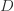 表示距离的阀值,在这里两个点之间的距离可以使用
表示距离的阀值,在这里两个点之间的距离可以使用 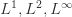 范数;
范数;
聚簇的质心定义为该类中所有点的平均值。i.e. 如果该类中的点是 ![A[0],A[1],\cdot\cdot\cdot,A[n-1]](http://mmbiz.qpic.cn/mmbiz_png/BNfPv196ib6fkRTS7C3H8CSSqUVnUvicR7IjJibSV2YBgenf91XlLZWFTV2ApKsA16KMZc85paibZKa0bLkhExqpcw/0?wx_fmt=png) ,那么质心就是
,那么质心就是 ![\sum_{i=0}^{n-1}A[i]/n](http://mmbiz.qpic.cn/mmbiz_png/BNfPv196ib6fkRTS7C3H8CSSqUVnUvicR7cqiab1X8ibDLngYxNWDj5OvwicHKdTOribwmx6Ard5HXJ6txkMsHJVk1Nw/0?wx_fmt=png) ;
;
第 j 个聚簇中元素个数用 ![num[j]](http://mmbiz.qpic.cn/mmbiz_png/BNfPv196ib6fkRTS7C3H8CSSqUVnUvicR7zd6aDesmycMqzOUZE9LoiazkHpJ4UIRVTZiamaArmvN5tRl5e1ro6kzg/0?wx_fmt=png) 表示。
表示。
方法:
Step 1:对于 ![dataMat[0]](http://mmbiz.qpic.cn/mmbiz_png/BNfPv196ib6fkRTS7C3H8CSSqUVnUvicR7DyX3qY2yNF6ahibIJLD0JUE0xxEUzWMd9ibD5ZXEoQpp33MQNm9WbtFg/0?wx_fmt=png) 而言,自成一类。i.e. 质心就是它本身
而言,自成一类。i.e. 质心就是它本身 ![C[0]=dataMat[0]](http://mmbiz.qpic.cn/mmbiz_png/BNfPv196ib6fkRTS7C3H8CSSqUVnUvicR7EmzkMcMVcP7mKt9w8xvl9jv42mPFn7ja38Pyj6XpYfja9KMZ21Yo3g/0?wx_fmt=png) ,该聚簇的元素个数就是
,该聚簇的元素个数就是 ![num[0]=1](http://mmbiz.qpic.cn/mmbiz_png/BNfPv196ib6fkRTS7C3H8CSSqUVnUvicR72QDUExqTjUW7icpAAibiayRNv5icygr60UEiaf9lt5dRm44trXly2rgA2VQ/0?wx_fmt=png) ,当前所有簇的个数是
,当前所有簇的个数是 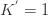 。
。
Step 2: 对于每一个 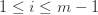 ,进行如下的循环操作:
,进行如下的循环操作:
假设当前有 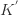 个簇,第 j 个簇的质心是
个簇,第 j 个簇的质心是 ![C[j]](http://mmbiz.qpic.cn/mmbiz_png/BNfPv196ib6fkRTS7C3H8CSSqUVnUvicR7ZK6mDzGPmCQ3haVJE5IVKiallxLTe6IdV8vVG1zuich6boNDLQ9ud2Kg/0?wx_fmt=png) ,第 j 个簇的元素个数是
,第 j 个簇的元素个数是 ![num[j]](http://mmbiz.qpic.cn/mmbiz_png/BNfPv196ib6fkRTS7C3H8CSSqUVnUvicR7zd6aDesmycMqzOUZE9LoiazkHpJ4UIRVTZiamaArmvN5tRl5e1ro6kzg/0?wx_fmt=png) ,其中
,其中 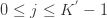 。
。
计算 ![d= \min_{0\leq j\leq K^{'}-1}Distance(dataMat[i],C[j])](http://mmbiz.qpic.cn/mmbiz_png/BNfPv196ib6fkRTS7C3H8CSSqUVnUvicR7duKQNCRVHribIxXxYMt3kQOOphghUxg4qBBsERCokN95p7Z2JS7yFtw/0?wx_fmt=png) ,其中的 Distance 可以是欧几里德空间的
,其中的 Distance 可以是欧几里德空间的 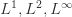 范数,对应的下标是
范数,对应的下标是 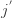 。i.e.
。i.e. ![j'=argmin_{0\leq j\leq K'-1}Distance(dataMat[i],C[j])](http://mmbiz.qpic.cn/mmbiz_png/BNfPv196ib6fkRTS7C3H8CSSqUVnUvicR7GOtdWsfe6K5j7w0yZicx8bFRKtYib6wKdapvFne20Q9EiaiabIxzpic28ibQ/0?wx_fmt=png) 。
。
(i)如果当前 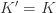 或者
或者 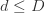 ,则把
,则把 ![dataMat[i]](http://mmbiz.qpic.cn/mmbiz_png/BNfPv196ib6fkRTS7C3H8CSSqUVnUvicR7muN5ibDVzP0RDBBcFaByw5s0icpVWItg74HDC1c7jPTfbcs95ksxaI5w/0?wx_fmt=png) 加入到第
加入到第 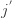 个聚簇。也就是说:
个聚簇。也就是说:
质心更新为 ![C[j'] \leftarrow (C[j']*num[j]](http://mmbiz.qpic.cn/mmbiz_png/BNfPv196ib6fkRTS7C3H8CSSqUVnUvicR7VSwqHmjlEfIDXjb1HnylzGQjqds7R1VNF4ZCDpLkCTIORKkicPQ3rtw/0?wx_fmt=png) +
+ ![dataMat[i])/(num[j]](http://mmbiz.qpic.cn/mmbiz_png/BNfPv196ib6fkRTS7C3H8CSSqUVnUvicR750IYPQLJqggklg8ytpg3pgRAGxLQ4ScialbKzhN2jghzqwHtx0LIVfA/0?wx_fmt=png) +
+ 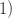 ,
,
元素的个数更新为 ![num[j'] \leftarrow num[j']](http://mmbiz.qpic.cn/mmbiz_png/BNfPv196ib6fkRTS7C3H8CSSqUVnUvicR7XMxXHvMTyw4M1HJGLmeIia8d2ibbmuI8y6N7iczQSZaGMbORfB7XzpbzA/0?wx_fmt=png) +
+ 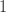 。
。
(ii)否则,![dataMat[i]](http://mmbiz.qpic.cn/mmbiz_png/BNfPv196ib6fkRTS7C3H8CSSqUVnUvicR7muN5ibDVzP0RDBBcFaByw5s0icpVWItg74HDC1c7jPTfbcs95ksxaI5w/0?wx_fmt=png) 需要自成一类。i.e.
需要自成一类。i.e. 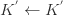 +
+ 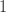 ,
,![num[K'-1]=1](http://mmbiz.qpic.cn/mmbiz_png/BNfPv196ib6fkRTS7C3H8CSSqUVnUvicR7Rxf6vibdn0UAIm7BhnIbM6nl15RAqrHOSnI8aSfGVXyFGFNANC6yCpw/0?wx_fmt=png) ,
,![C[K'-1]=dataMat[i]](http://mmbiz.qpic.cn/mmbiz_png/BNfPv196ib6fkRTS7C3H8CSSqUVnUvicR7EibqFNRDrbZicRvmUlQx0MDQPZ2Btm2iaJCV0TMvjjItPoxtwRAG8Mbjw/0?wx_fmt=png) 。
。
注:
(1)数据的先后顺序对聚类的效果有一定的影响。
(2)该算法的时间复杂度与簇的个数是相关的,通常来说,如果形成的簇越多,对于一个新的样本与质心的比较次数就会越多。
(3)如果设置簇的最大个数是一个比较小的数字的时候,那么对于一个新的样本,它需要比较的次数就会大量减少。如果最小距离小于 D 或者目前已经达到最大簇的个数的话,那么把新的样本放入某个类。此时,可能会出现某个类由于这个新的样本导致质心偏移的情况。如果设置 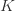 很大,那么计算的时间复杂度就会增加。因此,在保证计算实时性的时候,需要考虑到
很大,那么计算的时间复杂度就会增加。因此,在保证计算实时性的时候,需要考虑到 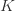 的设置问题。
的设置问题。
效果展示:
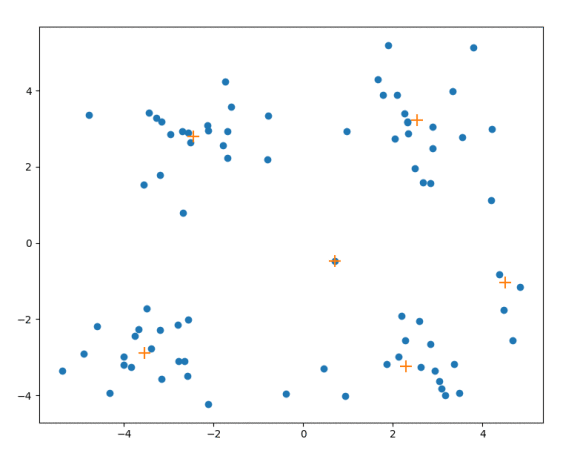
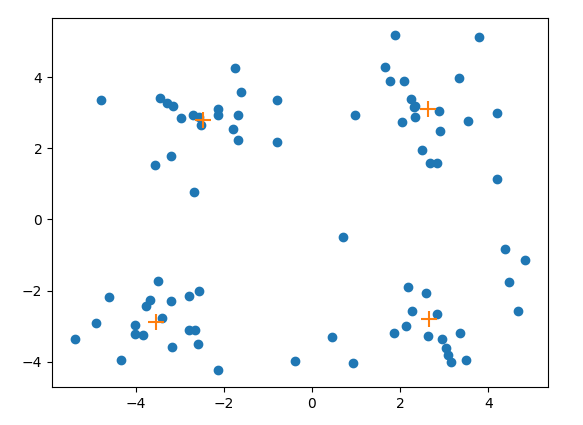
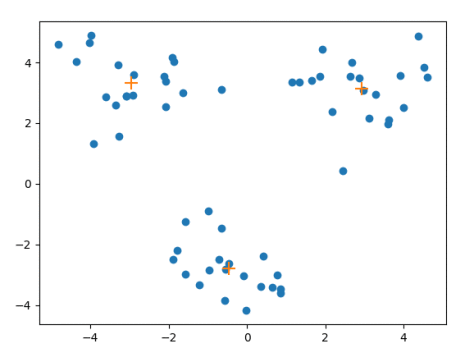
使用一批二维数据集合,进行流式聚类算法可以得到下图:’+’ 表示的是质心的位置,其余就是数据点的位置。通过选择不同的距离阈值 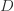 ,就可以得到不同的聚类情况。其中 ‘+’ 表示该簇质心的位置,蓝色的点表示数据点。如下图所示:
,就可以得到不同的聚类情况。其中 ‘+’ 表示该簇质心的位置,蓝色的点表示数据点。如下图所示:
欢迎大家关注公众账号数学人生
(长按图片,识别二维码即可添加关注)















