作者简介:吕坚平博士, 神经网络早期探索者之一,早在上世纪九十年代耶鲁大学攻读博士期间就开创性地结合神经网络与信号处理,在NIPS上发表的工作被工业界广泛使用。他先后在Nvidia、MediaTek和Intel担任资深架构师和资深总监的职务,现任异构智能(NovuMind)VP of Engineering。
近日Google在In-Datacenter Performance Analysis of a Tensor Processing Unit的论文中公开了TPU (Tensor Processing Unit) 的技术细节和基于脉动阵列 (Systolic Array) 的矩阵运算性能,该论文也成为了最近最热门的论文之一。TPU主要是围绕着基于脉动阵列的矩阵乘法器建制而成。但因为脉动阵列本身扩充性不高,我主张我们应该继续找寻其他替代方案。
为什么关注矩阵乘法?
Google 声称TPU在性能和能效比 (energy efficiency) 方面都优于CPU和GPU几个数量级,并把这归功于他们的DSD (domain-specific design ,基于应用领域的定制化设计)。另一方面,NVIDIA 在最近发表的博客文章AI Drives the Rise of Accelerated Computing in Data Centers中,以自家整理出来的性能报告回应,并强调无论是TPU还是GPU其主旨都是在加速深度神经网络 (Deep Neural Networks,DNN) 中的高维矩阵张量的计算。张量是用于表示深层神经网络层的高维数据阵列,深度学习任务可以描述为如下张量计算图:
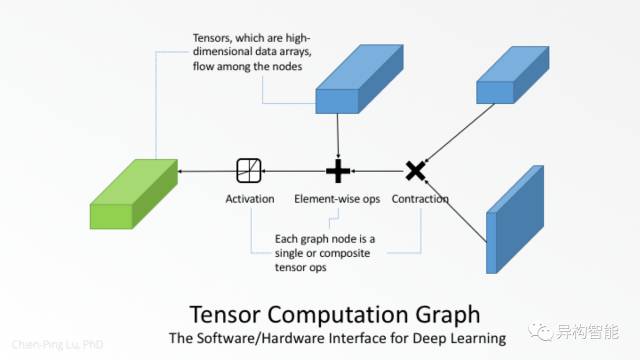
TPU 专门用于解决深度学习中的矩阵运算,而GPU最初是为图像渲染加速而开发,并逐渐演化成通用的并行计算单元。GPU能够为深度学习所用是因为它拥有高度优化的矩阵内码库 (matrix kernel library) , 尤其是曾经为高性能计算 (HPC) 开发的矩阵乘法。
当GPU被用于深度学习时,张量被展开成多个二维矩阵,矩阵运算是由从host CPU调用矩阵代码库完成的,矩阵代码库是针对GPU底层优化过的矩阵运算代码。尽管程序开发人员可以编写他们自己的代码,大部分人仍然会选择采用已经内置的矩阵代码库。这样的以矩阵为中心的方法 (参考论文:cuDNN: Efficient Primitives for DeepLearning) 可能是TPU设计团队以矩阵作为基础元件并把整个TPU建立在矩阵乘法之上的灵感来源。
为什么要用“脉动阵列”?
引人注目的是TPU设计团队选择使用脉动阵列。脉动阵列是一系列在网格中规律布置的处理单元 (Processing Elements,PE) 。脉动阵列中的每一个PE会以预定的步骤和它相邻的PE进行数据传输。脉动阵列中的每个PE 是MAC (Multiply-Accumulate Unit,乘加器); 在processor mesh中,每个PE是完整的处理器;而GPU计算集群中的PE是一个较简化的处理器,并与同一个集群中的其他PE共享前端和外设。在以上三种解决方案中,MAC单元的密度在脉动阵列中最高。这三者的不同可以在下图中看出:
尽管脉动阵列具有设计简单而规则,计算与I/O的耗时较平衡,容易实现高并行性且PE间通信较简单等优势,但是直到TPU的出现,脉动阵列才第一次真正商业化。真正令人印象深刻的是,TPU团队不仅让孔祥重院士 (H.T. Kung) 在1982年提出的一个古老的想法重燃生机而且性能突出,并且也构建了有史以来最大的脉动阵列。
“脉动阵列”可扩展吗?
虽然TPU设计的全部细节尚未得到充分披露,但TPU论文的作者给出了一些令人疑惑的结果,这让人对脉动阵列的可扩展性产生了疑问:
更大的矩阵乘法单元 (512*512) 不能帮助任何DNN
大的维度 (256*256) 的一小部分, 相对来说还是不小
笔者希望使用以下假设图解释这两个声明:
第一个结果似乎表示256*256,512*512维度单元在加速曲线的饱和区域。第二个陈述意味着128*128可能也在在饱和区。这表明,基于芯片上缓冲区大小和内存带宽,Google应该采用128*128或更小的单元的TPU,而不会导致性能下降。从128×128到512×512 (16倍),性能无法提升,可能是由于脉动阵列的不平衡设计或是脉动阵列本质上的限制。作为首次成功实现脉动阵列的应用,TPU有助于我们去发现更多的问题。
在用于矩阵A和B相乘的典型脉动阵列,矩阵B被划分成相同的正方形形状的阵列的方块。矩阵A的子矩阵只被加载一次,然后与B的多个方块相乘。因此,我们可以假定加载A需要的带宽相对较小。
在TPU里,输入矩阵为A,权重矩阵为B。根据对脉动阵列的理解,让我们分析脉动阵列难以扩展的原因:
1. 延迟会随着阵列边长成线性增长
TPU一文强调低延迟是用户要求的关键性·能指标,但是,当脉动阵列的边长增大2倍时,通过阵列的延迟会增加2倍。第一行输入的第一个元素需要256 周期来横向阵列,另外256个周期是第一个部分和 (partial sum) 向下遍历阵列并沿着累加的结果。当脉动阵列的边长从256倍增加到512时,通过阵列的延迟将从512倍增加到1024,如下所示:
2. 加载权重的开销在两个维度上变差
当输入子矩阵相对较维度较小时,执行时间主要由加载权重方块的时间决定。我们假设需要相同的时间来加载一个被充分利用的PE阵列和仅仅被部分利用的PE阵列。在下图中,对于512*512维的矩阵单元,方块未占用部分的总面积的开销要大于 256*256维:
这与TPU论文所述一致:
"The issue is analogous to internal fragmentation of large pages, only worse since it’s intwo dimensions. Consider the 600x600 matrix used in LSTM1. With a 256x256 matrix unit, it takes 9 steps to tile 600x600, for a total of 18 us of time. The larger 512x512 unit requires only four steps, but each step takes fourtimes longer, for 32 us of time."
3. 输入带宽需求随阵列边长平方增加
当输入子矩阵足够高时,我们来看一下这个例子。 B 个周期内,通过将B×512输入子矩阵与512×512维权重方块相乘,预计512×512维矩阵单元将比256×256维快四倍。由于相关的512×512 权重方块的数量是256×256方块的数量的1/2,所以与B×256相比,B×512子矩阵在TPU上只能停留1/2的时间。因此,它需要四倍的输入带宽来及时加载下一个B×512子矩阵,以达到所需的四倍加速。
4. 阵列的利用率随着阵列的边长的增长而减小
这通常发生在卷积神经网络(CNN)的其中一层,其中相应的矩阵乘法的内部维度的长度与特征深度相关。更大的阵列则可能被更少的占用,如下图所示:
总而言之,一个四倍于TPU单元的512×512维的单元将带来四倍大的权重方块,这可能对可扩展性造成如下影响:
延迟会成线性增长
加载权重的开销变差
它需要四倍的输入带宽来实现四倍加速
它使CNN的特征深度变得相对较浅
根据我们的观察,我们解释了512×512维单元不能帮助CNNo之类的受到计算限制的应用,可能的原因是:
1. 512×512维单元必须与四倍的输入带宽匹配,以达到所需的四倍加速。然而,输入通过PCIe总线输送到TPU。标准PCIe总线可能无法应付四倍输入带宽要求。因此,它可能会导致受到计算限制的CNNo成为受到PCIe限制。
2. 由于其特征层数少,CNN1在TPU上的性能较差。因为特征层数的多少与脉动阵列的边长相关,可能是CNNo的特征层数在512×512单元上相对变少。
我们应该拥抱脉动阵列吗?
TPU的成功,指出了使用矩阵作为基础单元来加速深度学习的机会与方向。然而,脉动阵列难以扩展,因为它需要带宽的成比例的增加来维持所需的加速倍数。这违反摩尔定律和储存速度落后于逻辑速度的技术趋势。另外它又使延迟变得更糟,这违反了论文中提到的用户需求的趋势。即使TPU中的矩阵乘法单元只是脉动矩阵乘法的多种选项之一,笔者认为相似的可扩展性问题将出现在任何商业实现中,这是因为来自
The curse of the square shape of a systolic array.
脉动阵列形状必须是正方型的限制
寻找芯片上矩阵乘法的可扩展替代方案不仅是为了构建更大的矩阵乘法单元以获得更好的性能,也是为了能用较小但使用率更高的矩阵乘法单元,来达成一样的性能水平。
根据TPU论文:
"As reading a large SRAM uses much more power than arithmetic, the matrix unit uses systolic execution to save energy by reducing reads and writes of the Unified Buffer"
在脉动阵列中,水平的脉动用于实现数据传播,而垂直脉动用于实现累加,如下图所示:
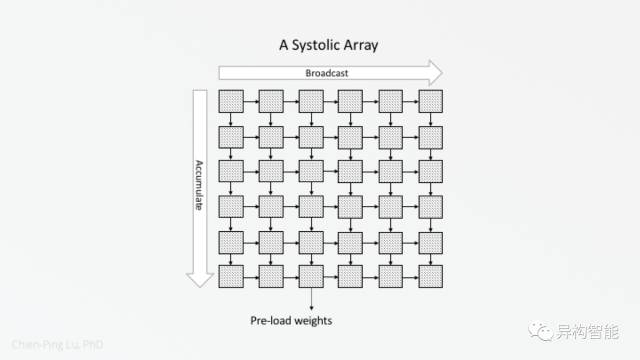
我们是否可以找到可扩展并且节能的替代方案,来实现所需的传播和累加而不以牺牲延迟时间为代价,这是一个值得思考的有趣的话题。
转载自 异构智能 公众号
欢迎关注异构智能公众号
NovuMind - Making Things Think!

本文由矽说原创,矽说旨在为大家提供半导体行业深度解读和各种福利您的支持是我们前进的动力,喜欢我们的文章请长按下面二维码,在弹出的菜单中选择“识别图中二维码”关注我们!

















