Google 面试题 | 种花

作者 | Ben助教+ 施助教

编辑 | Freya

专栏 | 九章算法

一个长条花坛里有若干并排的花槽，有些花槽中已经种了花，有些则还没种花。然而，不能将两株花种在相邻的花槽否则它们会争夺水分导致两者都枯萎。给定一个花坛的种植情况flowerbed（一个包含0和1的数组，0表示该花槽为空，1表示该花槽已经种了花），以及一个数n，问是否可以再种下新的n株花且满足相邻花槽不能同时种花的条件。

样例 1

输入： flowerbed = [1,0,0,0,1], n = 1

输出： True

样例 2

输入： flowerbed = [1,0,0,0,1], n = 2

输出： False

注意

输入数组本身满足相邻花槽不同时种花的条件。

输入数组的长度范围为[1, 20000]。

n是非负整数且大小不会超过输入数组的长度。

a. 为了尽可能的多种点花，应该使花种得尽量的密集。可以使用贪心的方法种花：从左往右扫描花槽，每遇到一个满足条件可以种植的花槽（前后花槽都为空或者为边界），就在这个位置种花，看能种下的花的数量是否大于等于n，是则返回true，否则返回false。一个小优化是当计数计到n时即可直接返回true。算法时间复杂度为O(n)，额外空间复杂度为O(1)。

b. Follow up：证明该贪心算法的正确性。证明贪心算法的正确性一般分为两部分：证明问题具有最优子结构（在这题中就是对于一个种植数量最多的最优种植方案，将方案中的一株花种下后得到新的花坛，方案除掉这株花之后得到到的剩余的方案仍是对于新花坛来说的最优方案），以及证明每一步的贪心选择一定属于某个最优方案。

http://www.jiuzhang.com/solution/can-place-flowers/

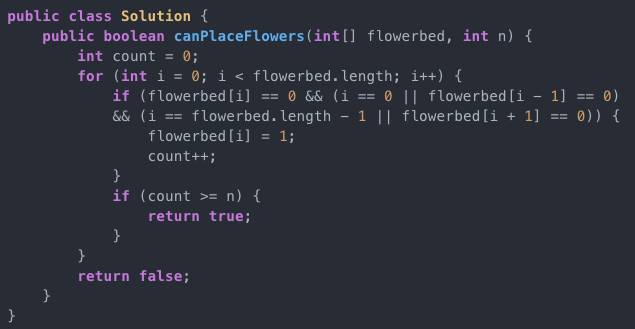
此题属于简单的贪心题，解题思路也很直观。给出正确的算法即可hire。

http://www.lintcode.com/zh-cn/problem/house-robber/