
原文来源
:
Towards Data Science
作者:Philip Osborne
「雷克世界」编译:嗯~是阿童木呀、EVA
导语:现如今,随着在强化学习领域的研究不断取得新的进展,实际生活中越来越多的问题可以用强化学习来解决。最近,数据分析师Philip Osborne在一篇文章中探讨了如何将强化学习应用于实际生活中的问题规划解决,希望能够为那些对此感兴趣的朋友提供一些帮助。
最近,我发表了一些实验示例,在这些示例中,我为一些现实生活问题创建了强化学习(Reinforcement Learning, RL)模型。例如,根据设定预算(Set Budget)和个人偏好(Personal Preference),使用强化学习来进行膳食计划。强化学习可以用于各种各样的计划问题,包括旅行计划、预算计划和商业策略。之所以使用RL是因为它的两个优点:它考虑了结果的可能性,并使得我们能够控制部分环境。因此,我决定写一个简单的示例,以便其他人可以考虑如何开始使用它来解决他们的日常生活或工作问题。
什么是强化学习?
强化学习(RL)是一个测试过程,通过基本的试错法(trial and error)测试哪种动作对环境的每个状态都是最好的。该模型引入了一个随机策略进行启动,每执行一个动作时,一个初始数量(称为奖励)就被馈送到模型中。这种情况一直持续到最终目标达成,例如,你赢得或输掉比赛,那场比赛(或那个事件)结束,比赛重新开始。随着模型经历越来越多的事件,它开始学习哪些行为更有可能引导我们取得正面的结果,因此,在任何给定的状态下都是最好的动作将会被称为最佳策略。
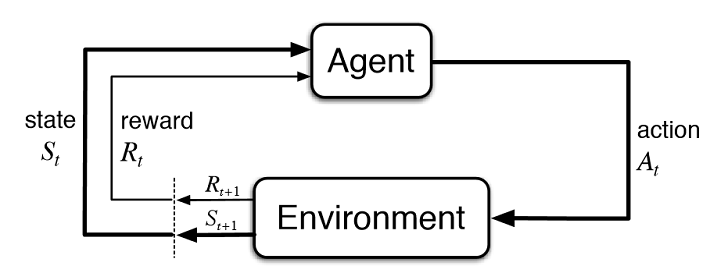
强化学习的一般过程
许多RL应用程序在游戏或虚拟环境中在线训练模型,模型能够反复地与环境进行交互。例如,你让模型对井字棋游戏(tic-tactoe)进行了一遍又一遍的模拟,这样它就能观察到成功和失败,或者尝试不同的动作。
在现实生活中,我们可能无法以这种方式训练我们的模型。例如,在线购物的推荐系统需要一个人的反馈来告诉我们它是否成功,并且基于有多少用户与购物网站进行交互,其可用性受到限制。相反,我们可能有一些样本数据显示了我们可以用来创建估计概率的时间周期内的购物趋势。使用这些方法,我们可以创建所谓的部分可观察马尔可夫决策过程(Partially Observed Markov Decision Process,POMDP),作为一种对潜概率分布进行泛化的方法。
部分可观察马尔可夫决策过程
马尔可夫决策过程(Markov Decision Processe,MDP)提供了一个框架,用于在结果部分是随机的且部分由决策者控制的情况下对决策进行建模。MDP的关键特性是它们遵循马尔可夫属性(Markov Property);对于给定的现状,未来的所有状态都独立于过去。换句话说,进入下一个状态的概率只取决于当前状态。
POMDP的工作原理类似,只不过它是MDPs的一种泛化。简而言之,这意味着模型不能简单地与环境交互,而是根据我们所观察到的结果给出一组概率分布。
我们可以在我们的POMDP上使用值迭代方法(value iteration method),但是在这个示例中,我们决定使用蒙特卡罗学习(Monte Carlo Learning)。
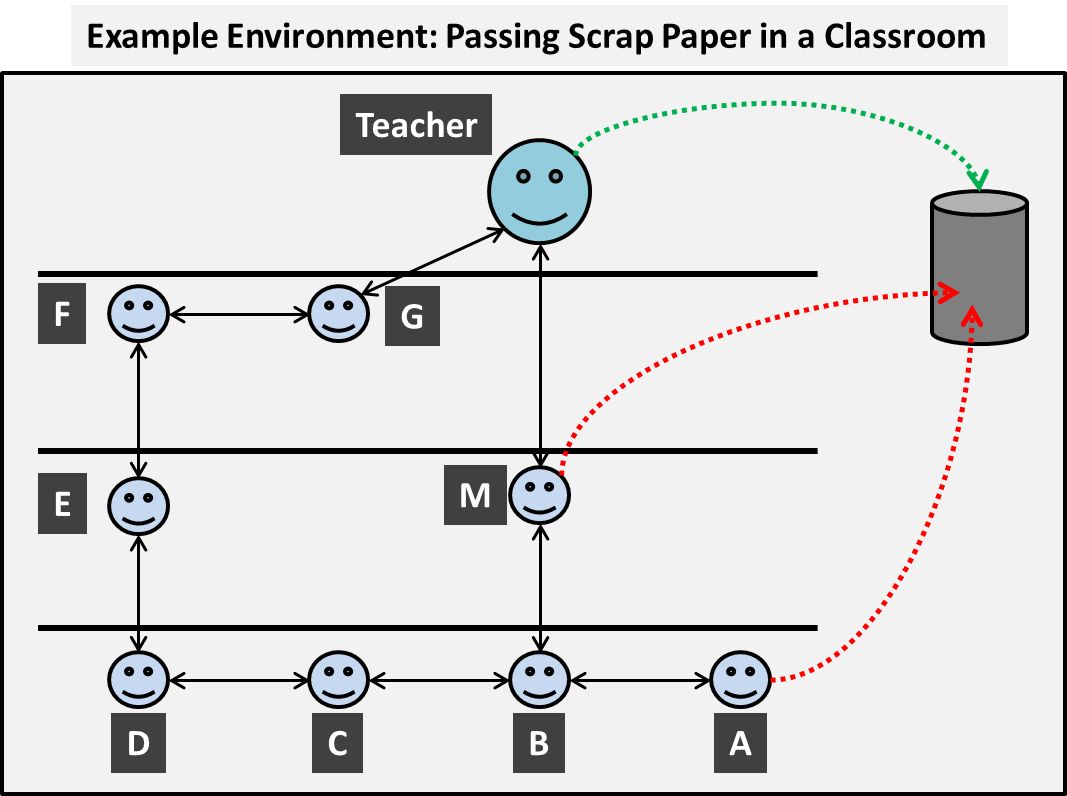
示例环境
想象一下子,你回到学校(或者仍然在学校),并且在教室里,老师对废纸有严格的规定,并且要求任何一张废纸都必须在教室前面传给他,他会把垃圾放入箱子(垃圾桶)中。然而,班上的一些学生对老师的规定并不在意,宁愿自己省去在教室里传递纸的麻烦。相反,这些觉得麻烦的人可能会选择从远处把废纸扔进垃圾桶。现在,这激怒了老师,而那些这样做的人受到了惩罚。这里引入了一个非常基本的动作奖励概念,我们有一个示例教室环境,如下图所示。
我们的目标是为每个人找到最好的指示,以便纸张到达老师那里,并被放置在箱子中,避免被扔进箱子中。

状态和动作
在我们的环境中,每个人都可以被认为是一种状态,他们可以对废纸做各种各样的动作。他们可能会选择把它传给近邻的同学,抓住它,或者有些人会选择把它扔进箱子中。因此,我们可以将我们的环境映射到一个更标准的网格布局上,如下所示。
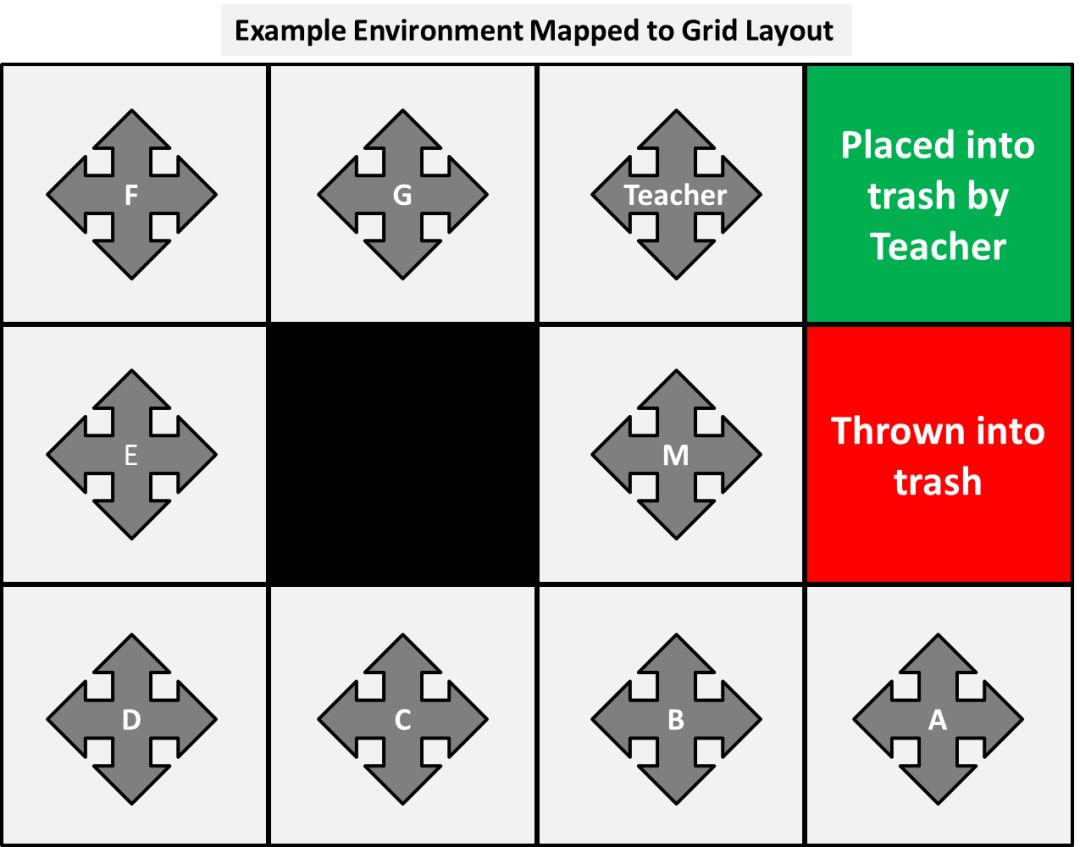
这是有意设计的,以使每个人或状态都有四个动作:上、下、左或右,每个都会根据谁做出动作而产生不同的“实际”结果。把人放入墙壁的动作(包括中间的黑色方块)表示这个人抓住了纸。在某些情况下,这个动作是重复的,但这在我们的示例中不是问题。
例如,人员A的动作的结果是:
上=扔进箱子
下=抓住纸
左=将纸传给人员B
右=抓住纸
概率性环境(Probabilistic Environment)
目前,部分控制环境的决策者是我们。我们会告诉每个人他们应该做出什么样的动作,这就是所谓的策略。
我在学习中面临的第一个挑战是理解环境很可能是概率性的,以及这意味着什么。概率性环境是当我们指示一个状态在我们的策略下做出动作的时候,有一个关于这是否能成功遵循的可能性问题。换句话说,如果我们告诉人员A把纸传给人员B,他们可以决定不遵循我们策略中的指示动作,而是把废纸扔进箱子中。另一个例子是,如果我们推荐在线购物产品,则不能保证该人员会看到每个产品。
可观察转移概率(Observed Transitional Probability)
为了找到可观察到转移概率,我们需要收集一些关于环境如何进行动作的样本数据。在我们收集信息之前,我们首先引入一个初始策略。为了开始这个过程,我随机选择了一个看起来会带来正面结果的。
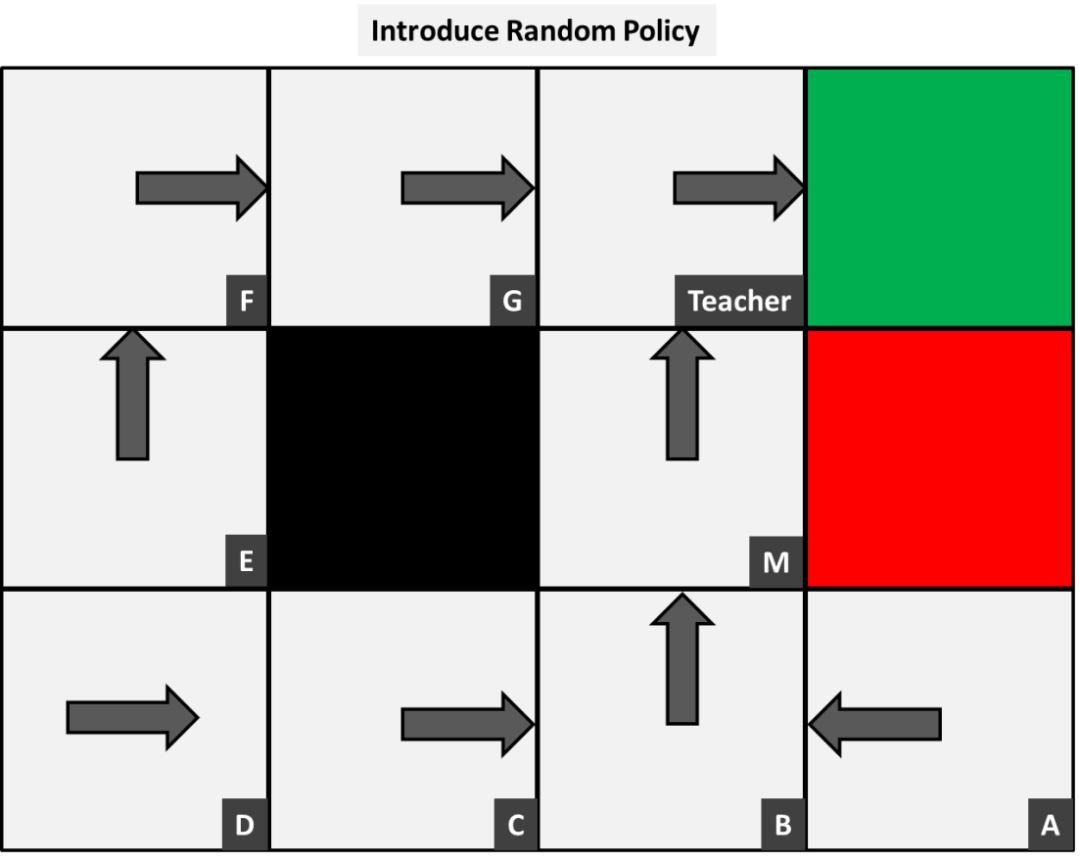
现在我们观察每个人在这个策略下所做出的动作。换句话说,我们坐在教室的后面,简单地观察这个课程,并观察了人员A下面的结果:
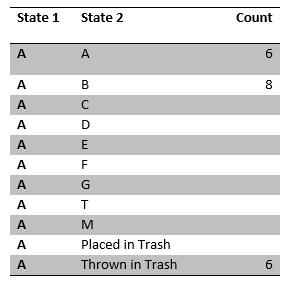
所观察到的人员A的结果
我们看到一张纸通过了这个人20次;6次他们一直抓着,8次他们把它传给人员B,还有6次他们将它扔进了垃圾桶。这意味着,在我们初始策略下,抓着或将其扔进垃圾桶的概率是6/20=0.3,同样,传递给人员B的概率为 8/20=0.4。我们可以观察教室其余的人来收集下面的样本数据:
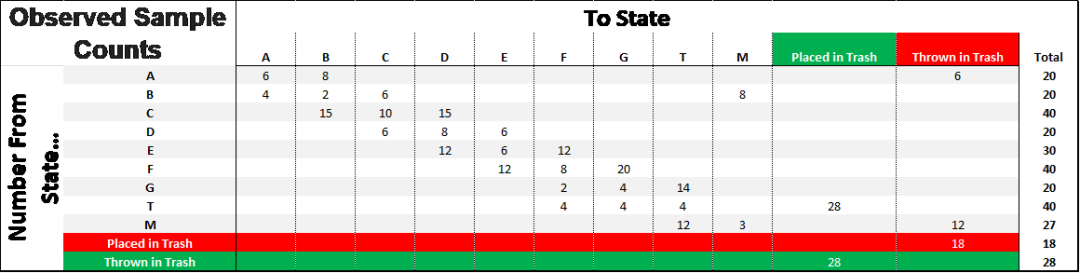
所观察到的实际结果
同样,之后我们计算概率为下面的矩阵,我们可以用这个来模拟经验。该模型的精确度将在很大程度上取决于概率是否是整个环境的真实表征。换句话说,我们需要确保我们有一个足够大且足够丰富的数据样本。
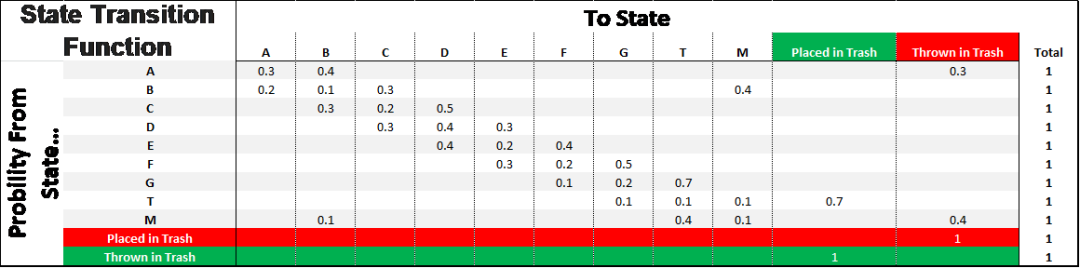
观察到的转移概率函数
多臂赌博机问题,事件,奖励,回报和折现率
所以我们有根据POMDP下样本数据估计的转移概率。在我们引入任何模型之前,下一步是引入奖励。到目前为止,我们只讨论了最后一步的结果;要么是老师把纸放到箱子里并得到一个正奖励,要么被人员A或人员M扔掉并得到一个负奖励。结束这个事件的最后一种奖励就是所谓的“终端奖励(Terminal Reward)”。但是,还有第三个结果也不太理想;这张纸不断地被传递,而且从来没有(或者比我们想要的时间长很多)到达箱子中。因此,总的来说,我们有三个最终结果:
·
纸被老师放到箱子里,并得到一个正的终端奖励
·
纸被一个学生扔到箱子里,并得到一个负的终端奖励
·
纸不断地在房间里传递,或者在学生身上停留的时间比我们想象的要长
为了避免纸被扔到箱子中,我们提供了一个大的负奖励,比如-1。而且因为老师在将垃圾放入垃圾桶时会很高兴,所以这会得到一个很大的正奖励,+1。为了避免它在房间里不断传递的结果,我们将所有其他动作的奖励设置为一个小的负值,比如-0.04。如果我们把它设为正值或空值,那么模型可能会让纸循环,因为获得小的正值比获得接近负值结果的风险要更好。这个数字也非常小,因为它只会收集一个终端奖励,但是它可能需要采取很多步骤才能结束这一事件,并且我们需要确保,如果纸张放到箱子里,正的结果不会被取消。请注意,奖励总是相对的,我选择了任意数字,但是如果结果不尽如人意,这些数字可能被改变。
虽然我们无意中讨论了这个示例中的一些事件,但我们还没有正式地定义它。事件就是每一张纸通过教室到达箱子中的动作,这是终端状态,结束了这该事件。在其他的示例中,比如玩井字棋游戏,你赢或输将是游戏的结束。
本文理论上可以从任何一个状态开始,这引出了为什么我们需要足够的事件来确保每个状态和动作都经过足够的测试,以使我们的结果不会被无效结果所驱动。然而,另一方面,我们引入的事件越多,计算时间就越长,而且根据环境的规模,我们可能没有无限的资源来做到这点。
这就是所谓的多臂赌博机问题(multi armed bandit problem):在有限的时间内(或其他资源),我们需要确保我们对每个状态—动作对进行足够多的测试,以至于我们的策略中所选择的动作实际上是最优动作。换句话说,我们需要验证以往带来好结果的动作不是纯粹的运气,而是事实上就是正确的选择,对于看起来很差的动作也是如此。在我们的例子中,这可能看起来很简单,我们有很少的状态,但想象一下,如果我们增加了规模,那么这将变得越来越成为一个大问题。
我们的RL模型的总体目标是选择最大化预期累积奖励的动作,即回报。换句话说,回报就是这一事件所获得的总奖励。计算这一点的一个简单方法是在每个事件中加上所有奖励,包括终端奖励。
一个更严谨的方法是通过在下面的公式中应用折扣因子γ来,并考虑该事件中的第一步骤要比后面的步骤更为重要:
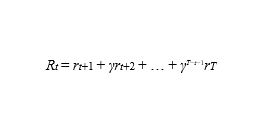
换句话说,我们将所有的奖励加起来,但是在后面的步骤中,以权衡gamma的方式来衡量它达到它们所需要花费的步数。
如果我们对示例进行新的考虑,使用折现回报将会使这一想象更为清晰,因为老师会奖励(或者相应地惩罚)参与这个事件的任何人,但是会根据他们与最终结果之间的距离来衡量。例如,如果纸张从A传递给B,再传递给M,即把纸扔进垃圾桶的人,那么M应该受到最大的惩罚,然后是B,因为是B把纸传递给他的,最后是A,他仍然参与最后的结果,但没有M或者B的任务重。这也强调,在一个状态下开始并且到达垃圾桶所需的时间越长(基于步骤的数量),得到的奖励或惩罚越少,但是为了采取更多的步骤也会累积更多的负的奖励。
在我们的示例中应用一个模型
由于我们的示例环境很小,因此我们可以应用每一个并显示手动执行的一些计算,并且说明更改参数所带来的影响。
对于任何算法,我们首先需要初始化状态值函数V(s),并决定将它们中的每一个的值设置为0,如下所示:

接下来,我们让模型根据我们所观察到的概率分布模拟环境体验。该模型在随机状态开始传递一张纸,在我们的策略下,每个动作的结果都是基于我们所观察到的概率。举例来说,假设我们有前三个模拟如下所示的情景:
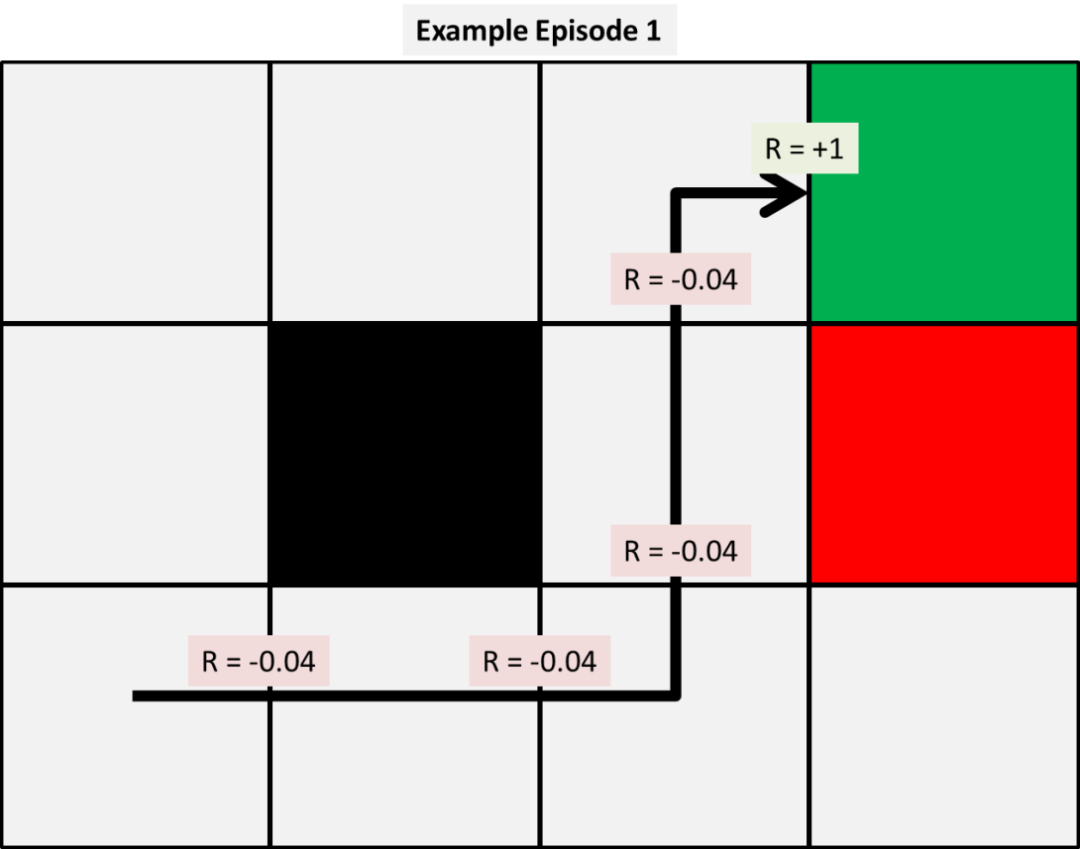
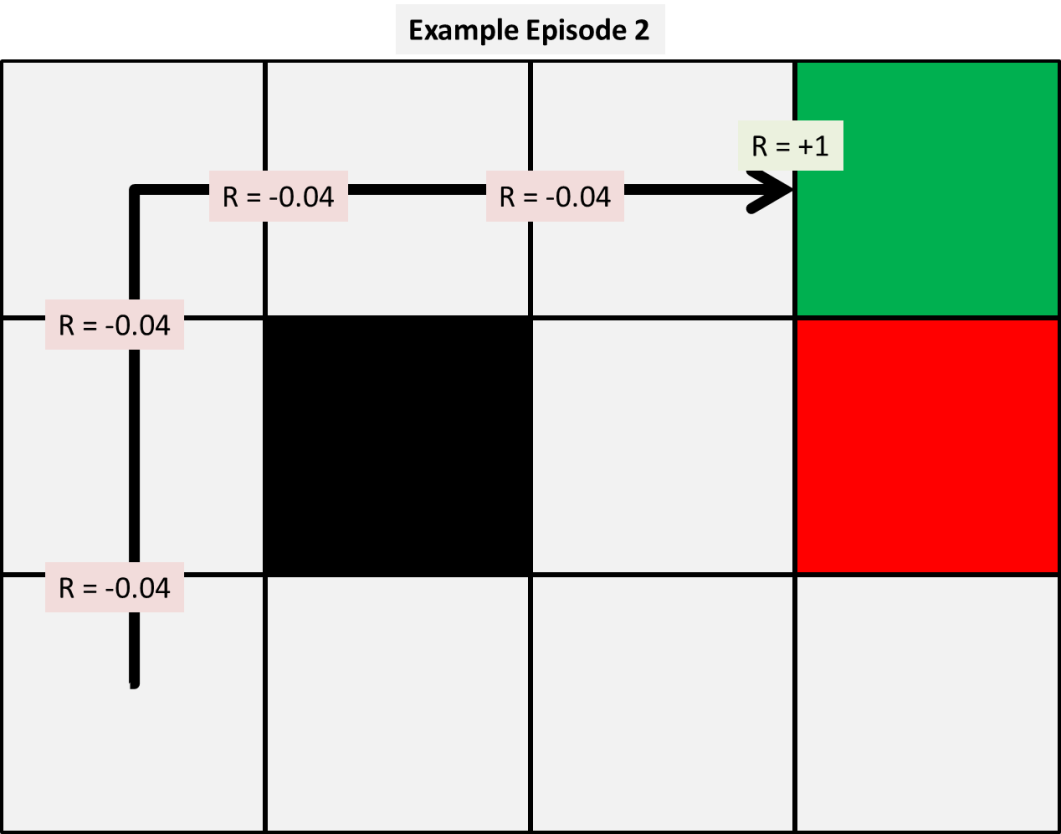
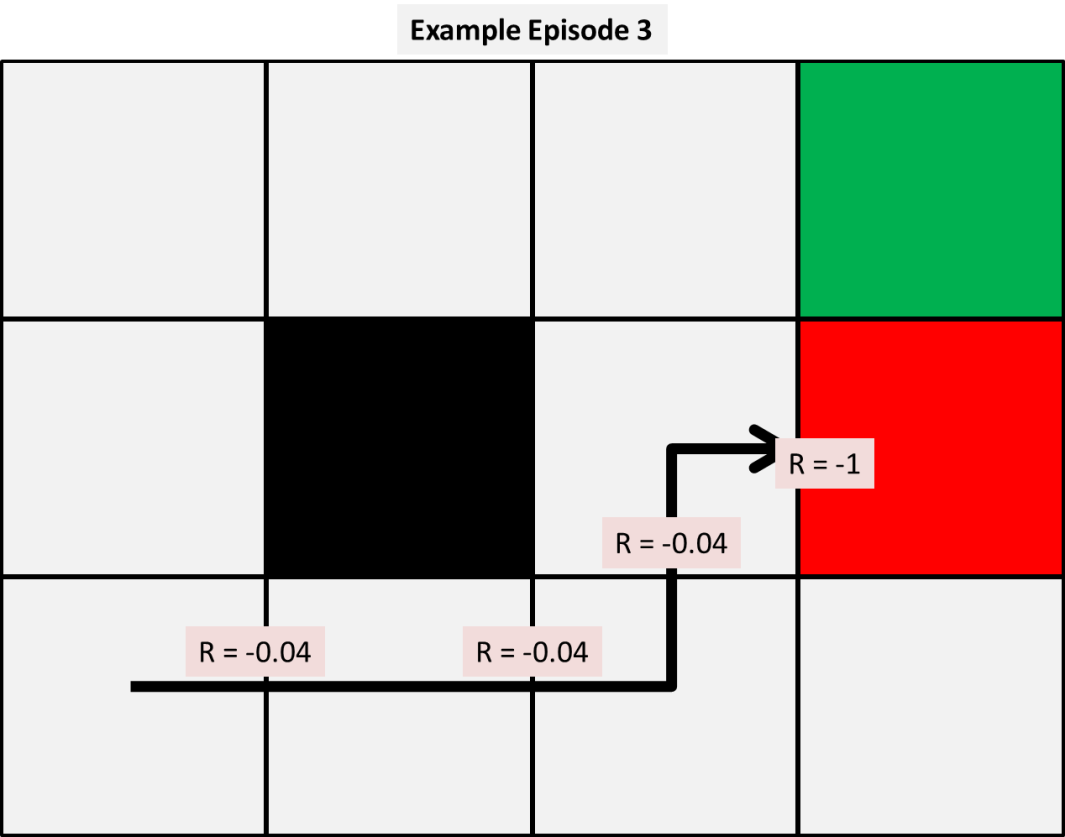
通过这些情景,我们可以使用给定的三个模型中的每一个来计算我们的状态值函数的前几次更新。现在,我们选择一个任意的alpha和gamma值为0.5,从而使我们的手动计算更为简单。稍后我们将会显示这个变量对结果的影响。
首先,我们应用时间差为0,我们模型中最简单的和前三个值更新如下所示:
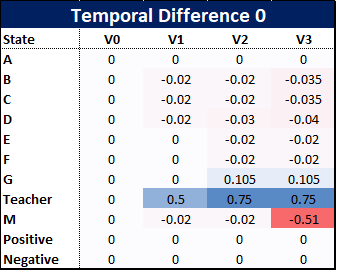
那么该如何计算这些值呢?因为我们的样本很小,我们可以手动显示计算结果。



那么在这个早期阶段我们可以观察到什么呢?首先,使用TD(0)对某些状态来说并不公平,例如一个称之为D的人,他在这个阶段中,三次中有两次没有从到达箱子中的纸张中得到任何东西。他的更新结果只受到下一阶段值的影响,但这强调了正奖励和负奖励是如何从角落向外传播的。随着我们进行的事件越来越多,正面的和负面的终端奖励将在所有的状态中进行进一步的蔓延。正如下面的图表中所看到的那样,这两个情节导致了一个正面的结果影响了教师和G的状态值,而单一的负面情景已经惩罚了一个称之为M的人。
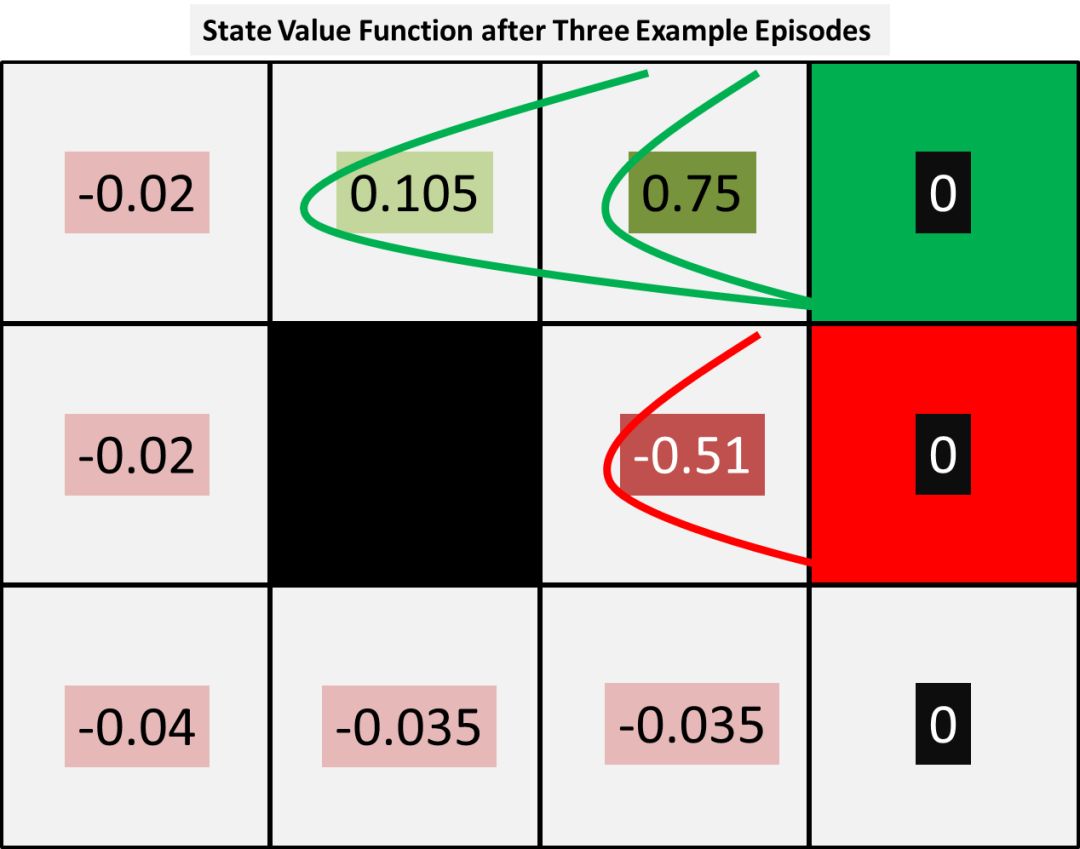
为了表明这一点,我们可以尝试更多的情景,并且如果我们重复已经给出的相同的三条路径,我们会产生以下状态值函数:
(请注意,在这个例子中,为了简单起见我们已经重复了这三个事件,但实际模型会有一些结果是基于所观察到的转换概率函数的事件)
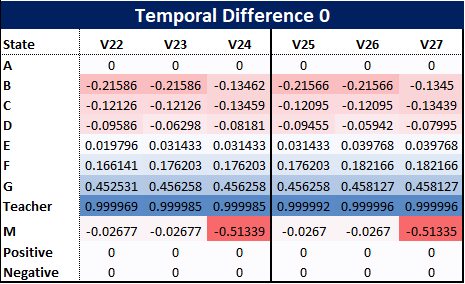
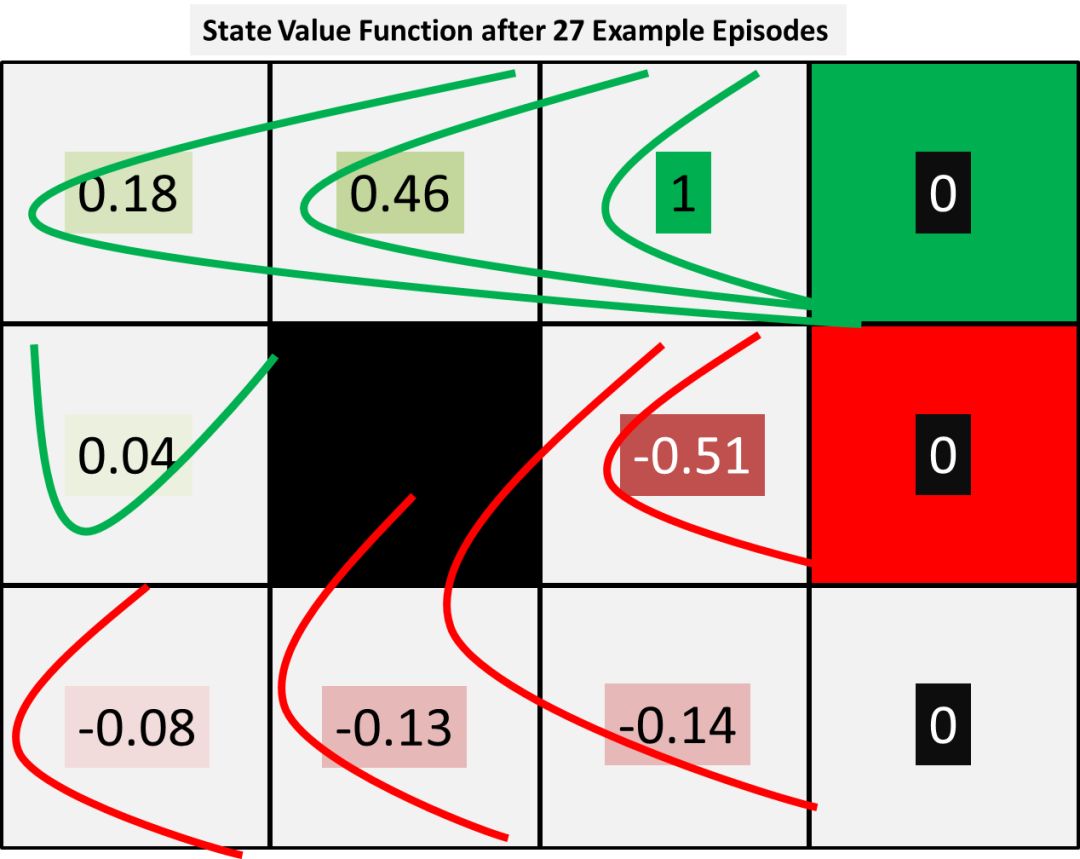
上图显示了从右上角向外传播的终端奖励。由此可见,我们可能会决定对策略进行更新,因为很明显,负面终端奖励已通过M,因此B和C也会受到负面影响。因此,基于V27,对于每个状态,我们可以决定通过为每个状态选择下一个最佳状态值来更新我们的策略,正如下图所示:
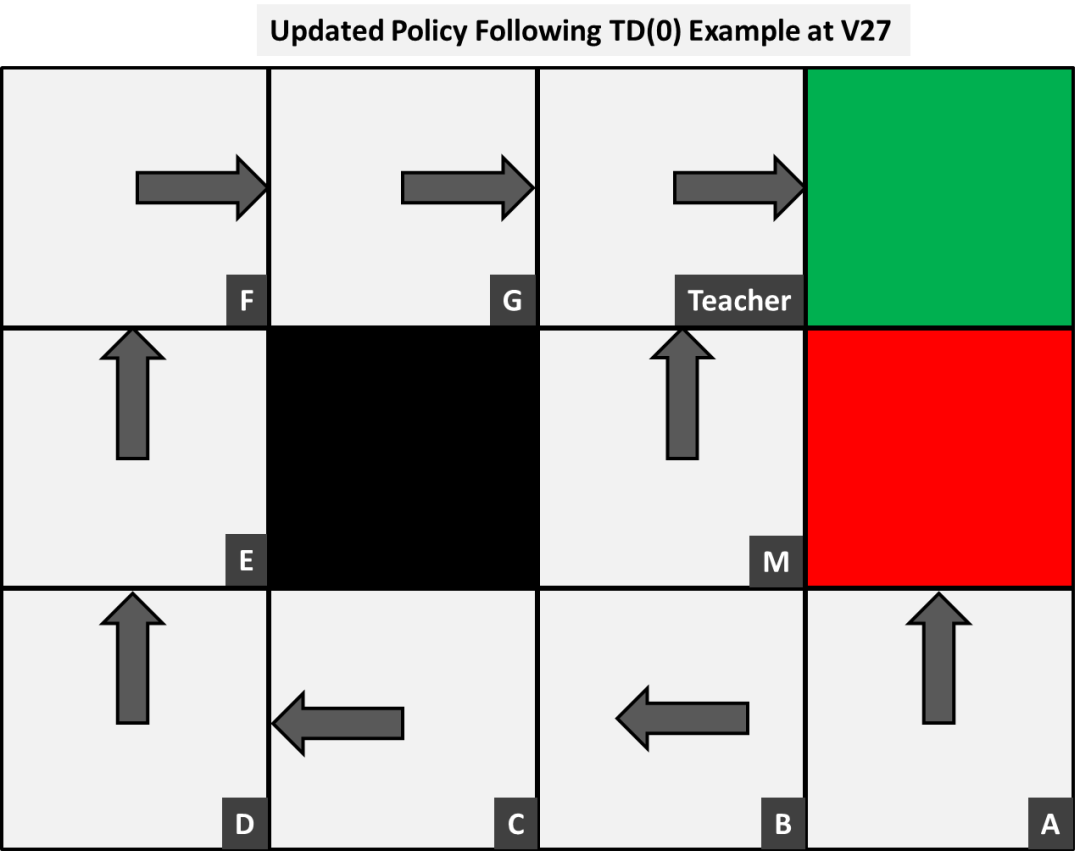
在这个例子中有两个原因需要引起注意,第一个是A的最好的动作是将其投入垃圾箱,并获得负面报酬。这是因为这些事件中没有任何一个访问过这个人,并强调多臂赌博机问题(multi armed bandit problem)。在这个小例子中只有很少的状态需要很多事件才能访问它们,但我们需要确保这些都完成了。这一动作对这个人更好的原因是因为这两个终端状态都没有值,正的和负的结果都在终端奖励中。那么,如果情况需要,我们可以根据结果将V0初始化为终端状态的数字。
其次,事件发生后,M的状态值在-0.03和-0.51(大约)之间来回切换,而我们需要解释为什么会发生这种情况。这是由我们的学习率—alpha造成的。目前,我们只介绍了我们的参数(学习率alpha和贴现率gamma),但没有详细解释它们将如何影响结果。大的学习率可能会导致结果发生振荡,但它不应该太小以至于永远不会收敛。这在下图中将进行进一步显示,它显示了每个事件的总V(s),我们可以清楚地看到,尽管有一个普遍的增长趋势,它在事件之间来回发散。学习率的另一个好的解释如下:
“在高尔夫比赛中,当球远离球洞时,球员会非常用力地击球从而球尽可能接近球洞。稍后当他到达被标记的区域时,他会选择一个不同的棍子来获得准确的短射门。因此,如果不选择短杆,他不可能将球放入洞中,他可能会在目标前进行两三次的传球操作。但如果他能够发挥最佳状态并使用适量的力量将球击进球洞,那将是再好不过的了”。
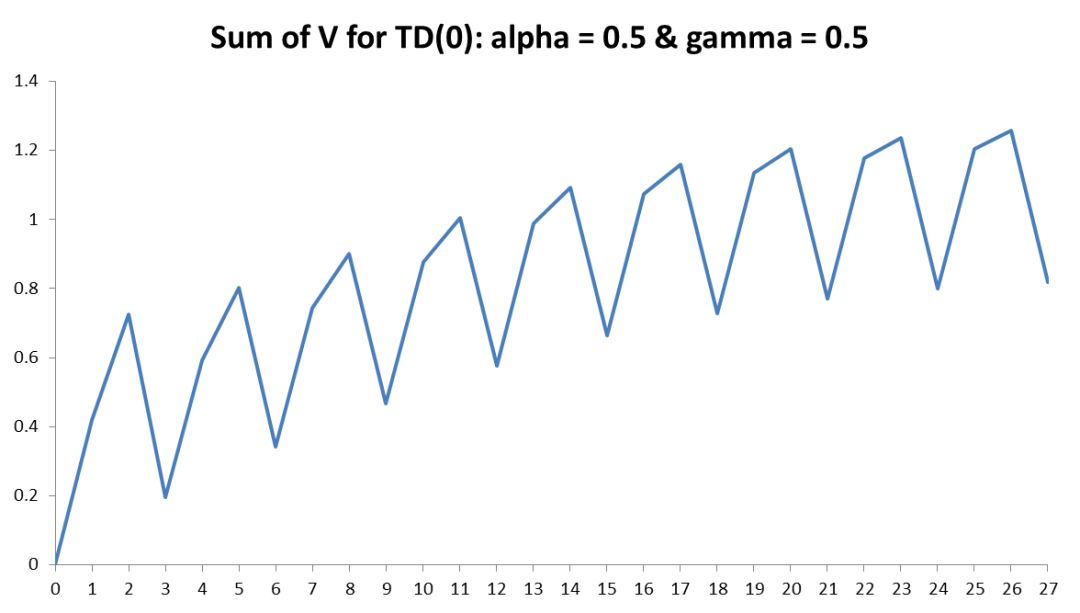
事件





