抖动是数字系统的信号完整性测试的核心内容之一,是时钟和串行信号的最重要测量参数(注:并行总线的最重要测量参数是建立时间和保持时间)。
一般这样定义抖动:“信号的某特定时刻相对于其理想时间位置上的短期偏离为抖动”(参考:Bell Communications
Research,Inc(Bellcore),"Synchrous Optical Network(SONET) Transport
Systems:Common Generic Criteria, TR-253-CORE",Issue 2, Rev No.1,
December 1997".如图1所示。
其中快过10HZ的偏离定义为抖动(Jitter),漫过10Hz的偏离定义为漂移(Wander)。
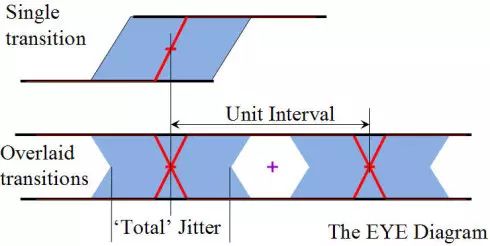
图1. 时钟和数据抖动的定义
抖动和相位噪声和频率噪声有什么关系呢?
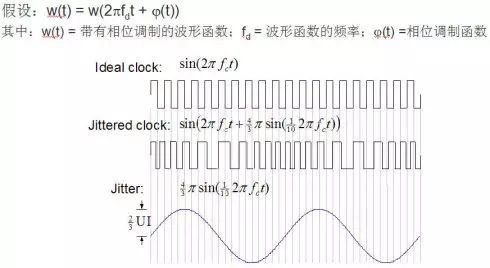

图2.抖动和相位噪声和频率噪声的关系
随着信号速率的不断提高和对精度的越来越高要求,需要进行抖动成分的分离以更深入表征抖动特征和查找问题根源。一般按图3进行抖动成分的分离。
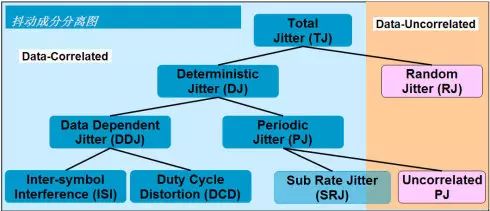
图3.抖动成分分离图
Total Jitter(TJ):总体抖动;
Random Jitter(RJ):随机抖动;
Deterministic Jitter(DJ):确定性抖动;
Data Dependent Jitter(DDJ):数据相关抖动;
Periodic Jitter(PJ):周期性抖动;
Inter-symbol Interference(ISI):码间干扰
Duty Cycle Distortion(DCD):占空比失真;
Sub Rate Jitter(SRJ):子速率抖动。
下面分别讨论每种抖动成分的特征和产生原因。
1、随机抖动RJ
随机抖动是不能预测的定时噪声,因为它没有可以识别的模式。典型的随机噪声实例是在无线电接收机调谐到没有活动的载频时听到的声音。尽管在理论上随机过程具有任意概率分布,但我们假设随机抖动呈现高斯分布,以建立抖动模型。这种假设的原因之一是,在许多电路中,随机噪声的主要来源是热噪声(也称为Johnson
噪声或散粒噪声),而热噪声呈现高斯分布。另一个比较基础的原因是,根据中心极限定理,不管各个噪声源采用什么分布,许多不相关的噪声源的合成效应该接近高斯分布。高斯分布也称为正态分布,但它的一个最重要的特点是:对高斯变量,它可以达到的峰值是无穷大。尽管这种随机变量的大多数样本将会聚集在中间值的周围,但在理论上,任何单一的样本,它可以偏离中间值任意大的量。所以,高斯分布都没有峰到峰边界值,从这种分布中的样本数越多,所测得的峰到峰值将越大。所以,我们用stdev或RMS(均方差)值来衡量随机抖动RJ。
2、确定性抖动DJ
确定抖动是可以重复的、可以预测的定时抖动。正因如此,这个抖动的峰到峰值具有上下限,在数量相对较少的观察基础上,通常可以以高置信度观察或预测其边界。DDJ和PJ根据抖动特点和根本成因进一步细分了这类抖动。确定性抖动和随机抖动在统计图上可以用图4形象化表示。
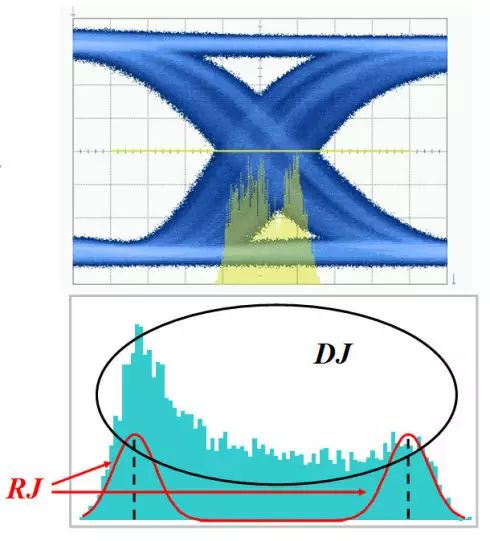
图4.RJ和DJ在统计图上的形象化表示
3、周期性抖动PJ和子速率抖动SRJ
以周期方式重复的抖动称为周期性抖动。由于任何周期波形都可以分解成傅立叶顺序的谐波相关的正弦曲线,这类抖动有时称为正弦曲线抖动。一般来说,周期性抖动与数据流中任何定期重复的码型无关。周期性抖动一般是由耦合到系统中的外部确定性的噪声源而引起的,如开关电源噪声或强的局部RF载波。时钟恢复PLL不稳定也可能会导致周期性抖动。图5是计算机中常用的SSC(扩频时钟)测试结果,SSC是典型的周期性抖动。子速率抖动SRJ是PJ的不同频率成分,可以帮助判断干扰源的频率。
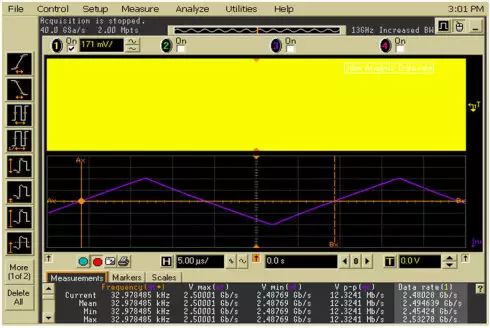
图5.SSC(扩频时钟)是典型的周期性抖动PJ
4、数据相关抖动DDJ
与数据流中的位序列相关的任何抖动都称为数据相关抖动DDJ。DDJ通常是由连接器,电缆,PCB传输线,背板等的不足的频响(阻抗不连续和损耗的综合结果)引起的。不足带宽对数据序列强烈地执行低通滤波,由于滤波,波形没到达完全的高状态或低状态,除非有同极性的多个位连续出现(注:轮流的1,0,1,0,1,0
属于高频,因为每单位区间内,信号都发生电压跳转。连续的1或0,因为信号电压一直维持固定,所以属于低频)。图6显示了这一个波形垂直偏置后与自己相叠加后的波形。可以看到,随着1,0,1,0,1,0,1
序列的下降跳转,比随着1,0,1,0,1,1,1
序列的下降跳转,跨过门限的时间较早。由于这种定时偏移是可以预测的,它与跳转前的特定数据有关,因此它属于DDJ,也称为码间干扰ISI。
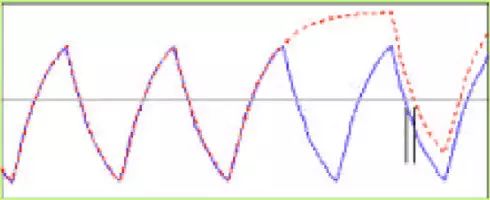
图6.码间干扰ISI的成因图示
5、占空比失真DCD
导致占空比失真DCD抖动的常见原因有两个:
1.
上升沿的转换速率与下降沿的转换速率不同。一般判定门限位于50%幅度点,但波形的上升时间慢,导致上升沿跨过门限的时间比下降沿晚,结果,在眼图上交叉点不是50%的位置,出现占空比失真抖动DCD。
2.
波形的判定门限高于或低于应该值。信号的眼图特征上,交叉点在50%,但是判定门限没有设在50%幅度点上也出现占空比失真抖动DCD,统计直方图看上去与原因1非常类似。
6、使用浴盆曲线和双狄拉克模型预估总体抖动TJ
高斯概率分布以及其峰到峰值在理论上没有界限,把这两项结合在一起考虑,会导致一个有趣的想法:对包含某些高斯抖动的任何信号,如果累计样本的时间足够长,眼图应该会完全合上。那么我们测试眼图和抖动测试多长时间、多少样本数比较合适?一般数字通讯的误码率BER要求为1e-12时(这是串行通信链路常用的误码率容限规范),而示波器要捕获这么多数据需要的时间太长,如何保证短时间捕获却能得出较准确的测量结果?这就要用到浴盆曲线和双狄拉克模型,图7的公式即是双狄拉克模型。
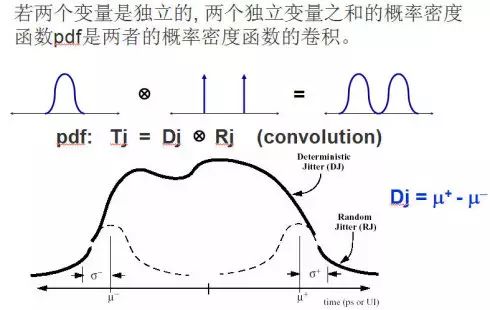
图7.双狄拉克模型和公式
使用示波器捕获足够的数据(一般不用太多,比如200K样点),可以容易分离出RJ和DJ,然后通过RJ和DJ卷积的双狄拉克模型,可以推算出误码率和眼张开度的对应曲线,从而可以推算出不同数据量或误码率对应的抖动值,如图8所示。浴盆曲线不是测试误码率的曲线,而是测试总体抖动的方法,这一点我们一定要正确理解。
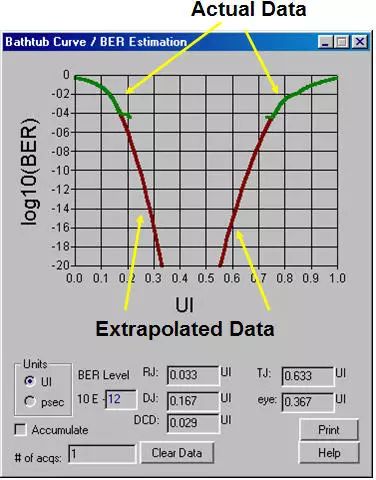
图8.通过浴盆曲线测试误码率为1e-12要求下的总体抖动TJ
本文转载自网络,如涉版权请联系我们删除
看完本文有收获?请分享给更多人
回复关键词有干货:电路设计丨电容丨三极管丨PCB丨接地‧‧‧‧‧‧
长按二维码识别关注

阅读原文可一键关注+历史信息















