用信息论构造出称球问题的解

提要：本文用信息论推导出称球问题的解，并构造了的递推操作的称量办法，彻底解决了任意个球的称球问题。 

关键词：称量 信息量 概率 递推 

经典的称球题目是这样的：“十二个外表相同的球中有一个坏球，它的重量和其它十一个好球不同，现在有一台没有砝码的天平，问需要称几次就能确保找出那个坏球”。 

（一）十二个球称几次

做过这道题目的人知道，答案是3次。不是太难，我们用图论中的策略树将称法记录如下：

称3次，从12个球里找到坏球，并知道坏球的轻重：

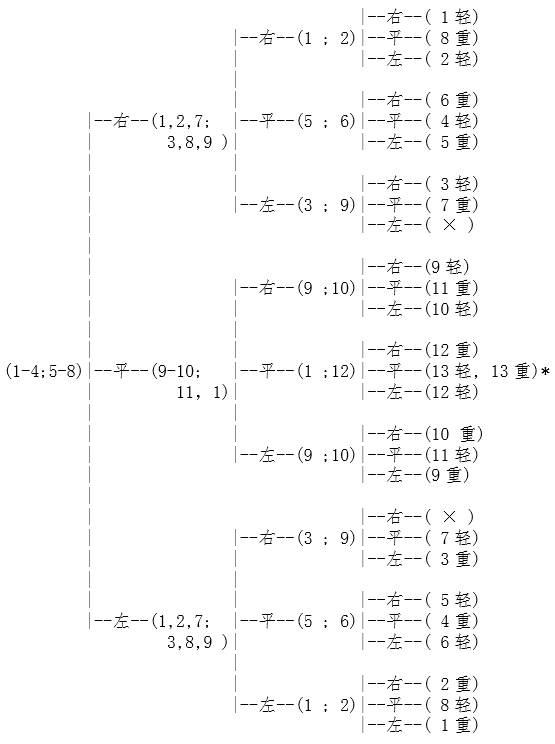
说明： 1、*号所在的一行对应十三个球的情形，留待后面分析13个球的时候使用，现在可以不管。

2、 树的每一处分叉就是一次称量，它有三个分支，分别标注了“右”、“平”和“左”，表示称量的结果为“右重”、“平衡”和“左重”。

3、 (1,2,3,4; 5,6,7,8) 或者(1-4; 5-8)表示“将1-4号放在左边，5-8号放在右边”这样的一次“称量”。无疑，天平两端球数不等时的称量没有意义。

4、(1重)和(2轻)表示 “1号是坏球，且较重，其他球都正常”和“2号是坏球，且较轻，其他球都正常”的最终结果；可以看出，在到达最终结果前经过了几个分叉，便是称量的次数。　　

这个结果是反复尝试得到的，虽然直觉上三次应该是最低了，但我们终究不能百分之百的确定，我们还是会问，两次能搞定吗？或者我们想，十三个球里面找一个坏球，三次可以吗？十四个呢？……，或者问，十个球里面找一个坏球要几次呢？二十个、四十个呢？N个呢？……还有，称三次最多可以从几个球里找到唯一的那个坏球？四次呢？五次、六次呢？M次呢？解这样的题目有规律可循吗？

一般的，我们要解决以下问题：给定任一自然数N，

⑴找出N个球称球问题所需的最小称量次数；

⑵给出最小次数称球的具体方法。

这道题的解决无非是要获得“十二个球中哪一个球是坏球的”的信息，是要确定一个事件集合里最终哪一个事件发生的过程。下面，我们用信息论的几个基本原理，试着分析一下。（随便找一本介绍有关香农信息论的书，都会有下面的内容，对信息论有所了解的，可以跳过下面一段）

香农在他创立的信息论中，将信息定义为对“事物不确定性的消除”，消除了多少不确定性，用信息量来衡量。一个事件集合中究竟发生哪一件事情就是不确定的，每个事件的发生都有一定的概率，比如明天天气可以由“晴、多云、阴、雨”几个事件组合而成，最终哪种天气会出现，今天是不确定的，今天只是知道明天各种天气的发生概率，并且知道所有各种天气出现的概率总和为1。我们来看看事件集合中发生某事件的信息大小和该事件发生的概率之间的关系。某事件发生的概率越小，该事件发生后给我们的“震撼”越大。比如“明天发生、不发生地震”这一事件集合中，明天不发生地震的概率远大于发生地震的概率，所以真的明天发生了地震，那我们所获得的信息量就比没有发生地震要大的多。此外，信息具有可加性，“今天地震了又下雨”给我们的信息应该是今天发生了地震和今天下雨两个事件的信息的和，而两个事件同时发生的概率又是这两个事件各自发生概率的乘积，基于此，香农将某一“发生概率为P”的事件的出现带来的信息量定义为1/P的对数，即1/P。基数r的不同，使得信息量可以有不同的单位，基数r=2，单位就是比特。比如抛一枚硬币结果是“国徽向上”的信息量是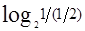=1比特。

好，我们仅用这一点信息理论，就可以解决上面提出来的那个称球问题了。我们的想法是，如果确定12个球当中的坏球需要的信息量是A，而从每次天平的称量结果可以至少获得的信息量是B，那不小于A/B的整数就应该是所需的最小的称量次数了。在称以前，十二只球的任何一个都可能是坏球，而且概率一样，都是1/12，所以称量最终确定了是哪一只后，我们得到了表征“坏球是12个球中的哪一个”的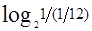=比特信息。另外，表明“好”球、“坏”球是以球的轻重为标准的，所以，如我们从前面策略树上看到的，最终的结果不仅是我们找到了坏球，而且知道了坏球比好球是轻了，还是重了，即不管我们是否需要，我们还获得了表征坏球是“轻”是“重”的=1比特信息。这样，根据信息的可加性，最终找到那只坏球以后，我们共计得到1+= 比特的信息量。

我们再来看一次称量所能给出的信息量。由于是无法码天平，称量能给我们的信息仅仅是天平的右重、左重、平衡三种状态。如果我们设计的称法能够让三种结果等概率出现，都为1/3，则我们就能够保证一次称量不管出现什么结果，我们都可以获得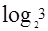比特的信息量。如果三个结果的概率不相等，由于三个结果的概率和为1，无疑，天平出现“发生概率”高的那种结果的话，我们就得不到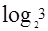比特的信息量。这样，对12个球，只要我们的称量办法能够让三种结果等概率出现，并且，称量次数M能够使得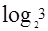M≥，即M≥/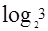=2.89，也就是3次，理论上，我们就能称出坏球。

所以，3次就可以从找到12球里面的找到1个坏球，并且，因为(1+)/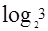=/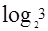=2.97，我们可以试着从13个球里面找一个坏球，看一看3次能不能称出来；而(1+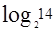)/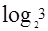=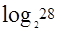/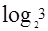=3.03>3，我们可以肯定3次是不可能确保从14个球当中找到一个坏球并知道其轻重的。如果是N个球，需要这样称M次，而我们所设计的称量办法可以让每次天平称量的三种结果等概率出现，那只要M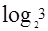≥1+，即M≥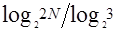=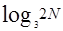,就一定能找到坏球。我们用{a}表示大于等于a的最小整数，则有M={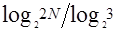=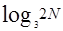}。如果M恰好等于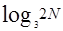，则N=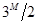。由于N必须为整数，故N最大只能为。

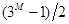所以，理论上，我们可以算出，用无砝码天平称2次、3次、4次、5次……，M次，最多可以从4个球、13个球、40个球， 121个球……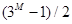，个球当中，找出一个不知是轻了还是重了的坏球。（结论1）

（二）寻求称量方法的预备问题

我们注意到，这个结果不是构造性的，也就是说，上面的结果只是给出了保证称出坏球的最低次数，但是它没有告诉我们如何去称。我们要知道的不仅仅是“需要称三次”，还要知道“如何称这三次”。总球数多了以后，反复尝试的办法就失效了。

从上面的分析可以看出，天平只有每种状态（右重、左重、平衡）出现的概率都为1/3的情况下，一次称量所给出的信息才能保证最低也是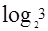比特，而如果称量的三种结果的概率不一样，出现“发生概率高”的那种天平称量结果的话，我们获得的信息量一定达不到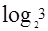，如何去称的问题实际上是如何实现天平称量的三个结果等概率（或者尽可能相近的概率）出现，这样即便天平给出的是最不利的结果（出现概率最大的称量结果），这次称量还能获得的足够多的信息量。保证天平三种状态相近概率出现，实际上就是全部的球如何分组称量的问题，即就是多少球放在天平的左盘，多少球放在右盘，多少球放在下面待称。现在，我们仍然从信息量入手来分析，作为准备，我们需要从一个更为简单的问题开始。

已知12个球中有一个坏球比正常的球重（或轻，分析的过程一样），用无法码天平要几次可以称出来。与前面的题目不一样的是我们已经得到了表征坏球轻重的=1比特信息。这时，找到坏球就只需要的信息，当然，我们还是要/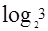=2.26次，也就是3次，但是/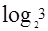=3，我们应该可以用3次称量从27只球当中找出一个已知较轻还是较重的坏球了。我们的想法是对的。称法很简单，假设坏球较重，将27个球编号1-27，取1-9,10-18号球，分别放天平的两侧，哪侧重则坏球便在哪侧的9个球中，比如天平平衡，则坏球在19-27号的9个球中。不管第一次称量结果怎样，再将包含坏球的那9个球等分成3个的三组，继续上面的称法，就得到包含坏球的一组3个球，取其中的两个再称一次，结果就出来了。可以看出由于每次都可以将包含坏球的那一组球等分成三部分，我们每次称量天平出现右重、左重、平衡三种状态的概率一样，那么每次天平称量结果给出的信息都是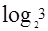比特，所以三次就正好获得所需的比特信息。

为了下面分析的需要，我们将题目变化得稍微复杂一些，并且将球的总数设为N：我们需要从N个球中找到一个坏球，我们不知道那个坏球是轻还是重了，但我们知道，如果坏球出现在N个球的前面X个球中，那一定是重了，如果出现在剩下的(N-X)个球中，那一定是轻了（把题目改成这样，纯粹是后面分析的需要），即我们只要知道了坏球是哪个，那坏球是轻是重就知道了，所以，找到坏球所需的信息量还是比特，用{ /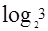}次称量一定可以称出来。

下面开始，叙述更加繁琐，如果大家对推导、证明过程没有兴趣，可以只阅读每节最后归纳的结论。

为了叙述的方便，我们将表述“坏球出现在N个球的前面X个球中，那一定是重了，如果出现在剩下的(N-X)个球中，那一定是轻了”想象成一次称量（X；N-X）的结果（我们在球数少的一侧加上标准重量的球），我们称这次想象的称量为第一次称量，即我们的第一次称量得到了坏球是轻是重的“分布”，这样，我们要研究的就是后续的第二次、第三次……的称量操作方法。

第二次称量的称法是这样的：我们尽可能将X个球均分成3组，这样各组之间的球数差不会超过1个。如果这3组中包含了坏球，那坏球一定是重了，故我们记为重组1、重组2、重组3。同样，余下的N-X个球，也这样分成3组，分别记为轻组1、轻组2、轻组3，如果这3组中包含了坏球，那坏球一定是轻了。我们分别取重组、轻组各1组，合成新的三部分，由于原来轻重各自组的球数差不会超过1个，这样适当的取组安排可以使得三部分的球数差也不会超过1。我们的目的是将要进行称量的球最为均匀地分成三部分（如果N是3 的正整数幂，那三部分的球数都相等）。比如，如果：重组1球数≥重组2球数≥重组3球数，轻组1球数≥轻组2球数≥轻组3球数，我们组合的三部分就可以是（重组1、轻组3）、（重组2、轻组2）、（重组3、轻组1）。我们对这三部分的球进行三种操作：1、“留”（指这部分球留在前一次“想象”称量时所在天平的盘中）。2、 “换”（指这部分球前一次“想象”称量在左盘的，现在要换到右盘；原来在右盘的，现在要换到左盘。3、“下”（指不管前一次“想象”称量在天平的哪一侧盘中，现在这部分球要拿到天平的下面）。我们可以分别称他们“留部分”、“换部分”、“下部分”。因为三部分球数差最多为1，这样我们完成上述留、换、下操作以后，左右盘的球数最多也只相差1个，所以，最多加上1个标准球，我们就可以进行这次称量。

进行这样操作的目的，仍然是为了这一次称量三个结果的出现能尽可能地等概率，它是前一次称量结果下的条件概率，不论这次天平称量是什么结果，我们都可以排除掉三部分中的两部分存在坏球的可能。如果这一次称量，天平的倾斜方向与第一次称量结果相同，那坏球一定在“留部分”当中；如果这一次称量，天平的倾斜方向与第一次称量结果相反，那坏球一定在“换部分”当中；如果天平平衡，那坏球一定在天平“下部分”球当中，三部分的球数对应着天平三种称量结果的概率。不管那一种结果，含有坏球的球的总数最多就只剩{N/3}个了，而且我们仍然知道，如果坏球出现在{N/3}个的哪些球中，那一定是重了；如果出现其他的球中，那一定是轻了。

接着我们对这{N/3}如法炮制，分成6各组，再组合成3部分，称量之后，含有坏球的总数就剩{{N/3}/3}个了……,如此下去，只要{}={/}次称量（如果N是3 的正整数幂，那就正好是/次），就可以从N个球当中找到坏球了，或者说，M次称量最多可以从个球当中找到一个已知坏球轻重“分布”的坏球。

归纳一下：

如果我们知道，坏球出现在N个球的前面X个球当中，那它一定是重了；如果出现在余下的N-X个球里面，那一定是轻了，用没有砝码的天平，称1、2、3、4……M次，能够确保从3、9、27、81……个球中找到坏球。我们有称量的可操作的方法。（结论2）

（三）十二个球的称法

至此，我们可以完整地构造出称球问题的称量方法了。

首先，12可以被3整除，无疑第一次称量要将12个球分成了4、4、4三组，天平的左盘、右盘、下面各放一组。

一、天平倾斜（由于右重、左重两种情况是对称的，我们只分析左重的情况），坏球在天平上的8个球里面，而且知道如果坏球在左边4个球的话一定是重了，在右边的4个球里的话一定是轻了，它是前面第二节分析过的情况，我们用结论2，再两次就可以称出坏球是8个球里面的哪一个了。

二、天平平衡，则坏球一定在天平下面的4个球里。第二次称量我们有三种称法：（1左、1右、2下）；（2左、1+S右、1下）；（1+S左、2右、1下）（+S表示从第一次称量已经知道的8个好球里面拿一个加到天平上,参与称量。同样，后面的两种称法是对称的，下面作为一种分析）。算一下每一种称法各个结果的信息量。第二次称量第一种称法（1左、1右、2下）：如果天平平衡，坏球在下面的2个球里，我们获得的信息量：（1+）-（1+）=1比特，即还剩余1+=2比特信息留到第三次称量；如果天平右重（或左重），坏球一定在天平上的两个球里，而且有了坏球的轻重的信息，则获得信息量是（1+）-=2比特，剩余=1比特信息。第二次称量第二种称法（2左、1+S右、1下）：如果天平平衡，我们知道坏球就是下面的那个球，获得了（1+）-（1+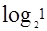）=2比特信息；如果天平倾斜，坏球在天平上的三个球里，而且有了坏球的轻重的信息，我们获得（1+）-=比特信息。我们现在要考虑的是两种分组称法各自最不利情况下的信息量，即要比较的是两种称法下各自获得的最低信息量。无疑，第二种称法是可行的，天平称量的三种可能结果中的最低信息量有 比特，比前一种分组下三种称量结果的最低信息量1比特要大，所以应该选择第二种称法（2左、1+S右、1下）。顺便说一下，第一种称法（1左、1右、2下）两种结果下，最多剩余的信息量还有2比特（原因就在于这次称量三种结果的概率太不均匀，剩余的信息量太大），是不能用剩下的第三次，也就是最后一次称量得到结果的，所以，第二次称量只有第二种称法才是可行的。

最后，剩下的第三次称量很简单，如果是第二种称法的第一种结果，天平平衡，从其他的11个球当中取一个（好球），称一下剩下的这只坏球，坏球的轻重就知道了。如果是第二种结果，一次称量三个已知坏球轻重“分布”的方法，还是用结论2，也不用说了。（参见前面给出的策略树）

从上面的称量办法可以看出，天平的第一次倾斜就给出了坏球轻重的1比特信息。我们从信息的可加性很容易理解这一点。我们将坏球是哪一个和坏球是轻是重两种信息分开看，假设第一次称量时我们已经得到了哪一个是坏球的信息，知道了坏球是天平上的哪一个球，那第一次称量天平的左斜还是右斜不就告诉了我们坏球是轻是重了吗？其实，我们得到的结论2也说明了这一点。

归纳一下：我们有了12个球找到坏球的称量操作办法，即尽可能将要称量的球按球数均匀分组，每次称量，以三种称量结果给出的最低信息量，对球各种分组方法的称量进行比较，取最大者所指示的办法，完成这次称量。

（四）十三个球的称法

按照“每次称量要获得最不利结果情况下的最大信息量”的原则对球进行分组，我们终于有了称球问题的可操作的解决办法。现在把这一结论推广到13个球。

第一节分析过了，从信息量的角度看，称量三次，最多可以从13个球当中找到一个不知是轻了还是重了的球。我们将要称量的13个球尽可能均匀地分成三组，最为均匀只能是4、4、5。由于天平两边的球数相等，称量才有意义，我们将球数为4的两组分别放到天平的两端进行第一次称量，但是我们马上就看到，如果此时天平平衡，坏球一定在剩下的5个球当中，而根据结论1，用剩下的2次是无法称出坏球的。我们再对上面的称法作一下信息量的分析，由于第一次称量我们只获得（1+）-（1+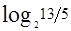）=，达不到一次称量所能获得的最大信息量，而剩余的信息量1+ >2，所以剩下的两次就不可能再称出坏球并知其轻重了。（其他的分组方法更为不均匀，比如5、5、3分组，如果天平倾斜，相当于我们要从已知坏球轻重的10球中找到坏球，根据结论2是不可能的）

现在我们退一步。由于剩余的信息量1+超过了两次称量所能获得的最大信息量，我们想是不是能够不要知道坏球的轻重，而仅仅把坏球找出来，这样我们所需的信息量应该只有，低于两次称量所能得到的信息量2了。果然可行，称量方法如下，其中S表示已经在第一次称量中已经知道是好的球：

称两次，从5个球里找到坏球，不需要知道坏球的轻重：

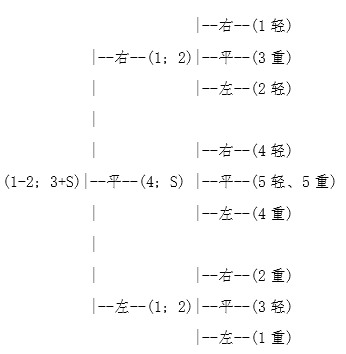
*说明：天平两次都是平衡的情况下，我们就无法得到坏球是轻是重的1比特信息，前面12球的策略树上，我们加上了这种情况。

就是说，不需要知道坏球是轻了还是重了的话，称量3次我们也能确保找到坏球，只是不能确保知道坏球的轻重。

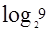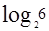注意这里的结果（不要知道坏球轻了还是重了的称量结果）和已经知道坏球的是轻是重的称量结果的不同。对于相同的总球数N，虽然最终获得的有用信息是一样的，都是（两种情况下都不再需要坏球是轻是重那1比特信息了），但是，是否事先知道“坏球是轻是重”这一信息，对称量能获得的有用信息影响很大。我们用N=9个球进行的第一次称量做个说明。无论我们是否知道“坏球是轻是重”这一信息，按照前面的分析，我们的分组都应该是（3左，3右，3下）。如果我们知道“坏球是轻是重”这一信息，那按照结论2，天平的任何称量结果都给出了比特信息，再有一次称量我们就可以找到坏球了；而如果我们不知道“坏球是轻是重”这一信息，天平平衡我们得到比特信息，天平倾斜我们获得了1+-=1+比特信息，但是由于不再需要坏球是轻是重那1比特信息了，此时，最终的有用信息只有，剩余的信息有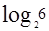，再有一次称量是不能找到坏球的。所以，总球数一样，“不要知道坏球轻了还是重了”的称量次数和“已经知道坏球的是轻是重而不需要知道坏球轻重”的称量次数不一样，虽然最终获得的有用信息是一样的。“坏球轻重”的信息在称量的过程中起了作用。

违背了结论1,十三个球不能三次称出坏球或者找到了坏球却不确保知其是轻了还是重了的原因，是第一次称量没有获得足够大的信息（13球无法平均分成三组），因为天平上的球必须是偶数，这样我们只能在天平上放8个球。按照结论2，余下的两次称量最多可以从9个球当中找到知道轻重的坏球，所以，如果我们事先手上有一只已知的好球，可以叫它标准球（它与好球有相同的质量，但我们一眼可以将它和其它13个球区分开来，比如它有不同的颜色），我们就可以在天平上放9个球，加上这只标准球，我们的第一次称量的球的分组变成（5右、4+S左、4下），此时，如果天平倾斜，我们获得（1+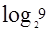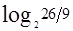）-=比特信息；如果天平平衡，我们获得（1+）-（1+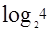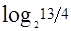）==比特信息，通过添加一只标准球，我们的第一次称量获得了更为均衡的信息量，三种结果都比前面（4左、4右、5）出现天平平衡情况的信息量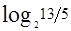要多。所以标准球的加入，“改善”了称量的手段，使称量结果给出的信息量更为均匀。

这样，有了标准球，将13个球按照（5右、4+S左、4下）分组，天平平衡，仿照12个球的方法，我们可以从边上的4个球里称两次找到坏球（参见本文开始给出的策略树）；天平倾斜，按结论2，我们可以从天平上的9个球称两次找到坏球。不管第一次称量的结果如何，余下的两次称量，一定可以找到坏球，而且知道坏球轻重，这样我们就彻底解决了13个球的问题。

我们注意到，额外的标准球只需要在第一次称量时使用，第一次称量完成后，我们就可以知道原来的13个球当中哪些是好球，而可以将他们作为标准球了。

归纳一下：要么找到的坏球不确保能知道它的轻重，要么我们事先有一只标准重量的球，只要具备这两个条件之一，我们就可以通过3次称量，找到13个球中的坏球。 

（五）N个球的递推称法

从13个球的称量办法，我们可以看到，有了标准球，“13个球里称3次找到一个不知轻重的坏球”可以分解成“4个球里称2次找到一个不知轻重的坏球”和“9个球里称2次找到一个已知轻重‘分布’的坏球”。13个球的第一次称量（5右、4+S左、4下）可以写成（9；4）。同样，“13（9+4）个球里称3次找到一个不知轻重的坏球”加上结论2当中的“27球里称3次找到一个已知轻重（分布）的坏球”又可以作为“40（27+13）个球称4次找到一个不知轻重的坏球”问题的第一次称量。我们可以将40个球按照（14右、13+S左、13下）或（27；13）分组，天平平衡，按上节的称法，我们可以从边上的13个球里称3次找到未知轻重的坏球；天平倾斜，我们可以从天平上的27个球称3次找到已知轻重（分布）的坏球，我们就解决了40（27+13）个球找到坏球的问题。

其实，有了标准球，“4个球里称2次找到一个不知轻重的球”一样也可以向前递归成分解成“1个球里称1次找到一个不知轻重的球” （实际上就是用标准球称一下这个球的轻重）和“3个球里称1次找到一个已知轻重（分布）的坏球”。（而如果没有标准球，如同3次从13个球里不能确保称出坏球轻重一样，两次我们不能确保称出4个球里的坏球轻重的）。

按照这样递推的办法，从N个球当中找到一个坏球，我们就有了下面的结论：有1个标准球，用无砝码天平，称量M次，我们最多可以从（-1）/2个球里面找到一个坏球，并且，知道它是比好球（标准球）轻了还是重了。我们的称量办法是：

将[（-1）/2-1]/3=(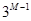-1)/2个球放在天平下面，而将剩下的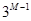个球加上一个标准球，分放到天平的两侧盘里。我们称之为称量[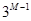;(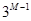-1)/2]。天平倾斜，问题归结为天平上面的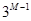个球称M-1次找到已知轻重（分布）的坏球的问题，我们用结论2可以解决；天平平衡，问题归结为天平下面的(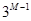-1)/2个球称M-1次找到未知轻重的坏球的问题……，如此逐次递推下去，称球问题得到解决。

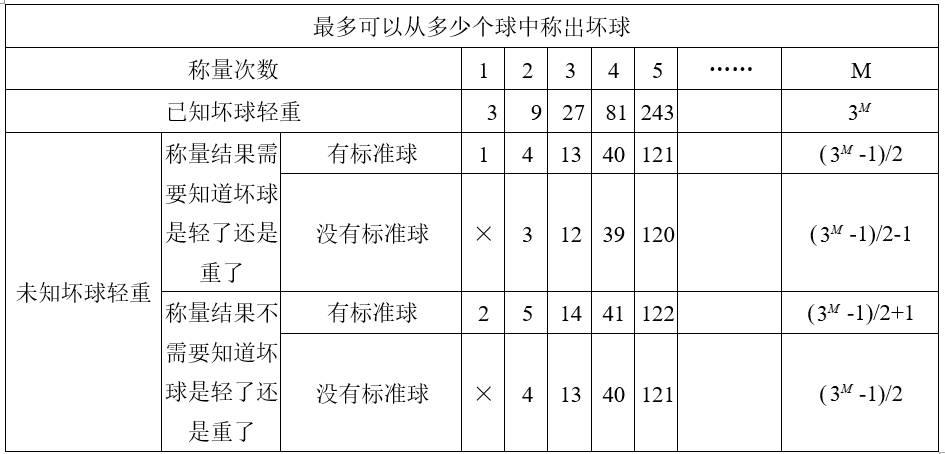
我们将结果汇总于下表。表中同时收进了“已知坏球轻重”、“有无标准球”、“是否需要知道坏球轻重”几种组合情况。 

表一：用无砝码天平称量M次最多可以从多少个球中称出坏球

我们从数学表达式可以很清楚地看出递归性。由于=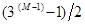+ ++…… +1= +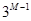，分组就是按照[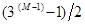;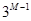]进行,将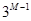个球加上一个标准球放在天平的两边，将个球留在天平下面，而= ++…… +1=+，这样的递归可以一直做到最后分组称量（1；3）。

如果总球数N在M次和M-1次称量所能找出坏球的最多球数之间，即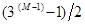,则我们一样留下在天平下面，剩下的如果是偶数，则天平的两边各取一半；如果是奇数则加上标准球后天平的两边各放一半，同样可以完成第一次称量，并递推下去。所以，上述的标准的称量办法就可以完成任意个球的称量，我们完整地拥有了找出“N个球当中的一个未知轻重的坏球”的严格的称量方法。我们将表一转换一下，得到表二；

表二：用无砝码天平确保找出N个球中的唯一一个重量不一样的坏球需要称量的次数

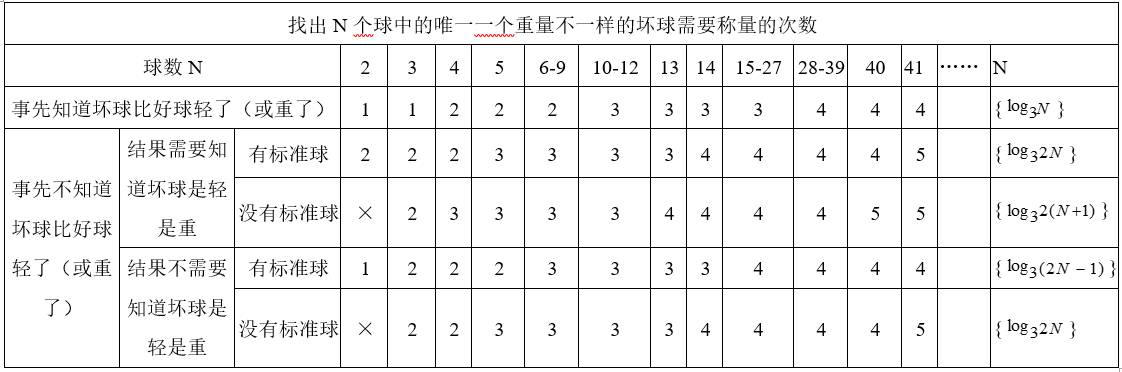
正如我们前面分析过的，同样的球数里面找到坏球，称量次数由于“有无标准球”和“是否需要知道坏球的轻重”的不同，可能是不一样的，原因就在于前者可以均衡称量各个结果的信息量，使最不利称量结果出现时的信息量达到最大；后者表明了我们需要获得的总信息量大小的不同。

顺便说一下，1个球里面找一个坏球，题目的意义仅仅是，如果我们有标准球，称一下这个球是轻了还是重了；2个球里面有一个坏球，也只有提供了标准重量的球才有意义。

归纳一下,对球数N大于2的称球问题：

1) N＜(-1)/2， M次称量就足够了； N=(-1)/2，M次称量能够确保找到坏球，但不能确保知道坏球比标准球轻还是重；如果另有一个标准球，那么称M次能够确保找到坏球，并知道坏球比标准球轻还是重；N=(-1)/2+1，只有在另有一个标准球同时不需要知道坏球比标准球轻还是重的情况下，才能确保找到坏球。具体如表一、表二所示

2) (-1)/2=(-1)/2 +，我们按照[(-1)/2; ]对待称的球进行分组，进行称量，天平倾斜，则应用结论2，完成称量；如果天平平衡，则再次将天平下面的(-1)/2 个球按[；]分组，进行称量。如此递推称量下去，便是解决称球问题的可操作的称量方法。 

（六）补充证明

前面对（12球、13球等）不同分组办法的称量结果的信息量进行了测算，其过程可以看成是用信息论对这些特例的称量办法作出的推导或证明。为严格起见，现在我们将证明推向一般，给出N个球的分组办法的证明。因为（M为称量次数）可以被3整除，为了下面表述的方便，我们以“没有标准球，同时需要知道坏球轻了还是重了”为例。其他三种球数的情况大同小异，只是由于总球数不能被3整除，表述起来困难一些。

如我们在上一节看到的，由于右重和左重是对称的，称量可以看成是将全部的球分成了两组，即天平上的一组（分到左右盘）和天平下的一组，我们再用信息论对分组球数进行推导。

设我们从N个球中留K个球在天平的下面，这样就有N-K个球分放到天平的两边盘中，如果

1、   天平倾斜（比如右重）我们获得的信息量为：;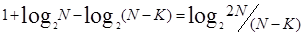

2、    天平平衡我们获得的信息量为：

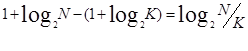
为使得两种结果所获得的信息量均衡，必须有：

即：

即我们取总球数的三分之一留在天平下面，而将其余的三分之二分放到天平上的两端去称量。当然，这一结果与前面递推称量办法采用的球的分组方法是一致的。 

（七）推广

我们用信息论彻底解决了“用没有砝码的天平在N个球当中找唯一一个重量不一样的坏球”的问题，这结论还可以作进一步的推广。我们可以猜测（他们的称法验证过于复杂）：N个球当中有K个坏球比其它球重了，而且这K个球重量一样，我们可以知道需要用无砝码天平称量次，就可以找到全部K个坏球；如果我们还不知道这K个球比其它球重了或者轻了，只知道这K个球重量一样，我们需要用无砝码天平称量，找到这K个坏球，并且知道他们是重了还是轻了；如果K个球有的比好球重，有的比好球轻，只是它们与好球重量的差距一致，那我们用无砝码天平称量，需要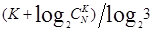次，才能找到全部K个球，并且知道他们各自是重了还是轻了……等等。上述各个结论对我们的实际工作，比如产品检测，应该还有一定的实际意义。

作者简介： 赵明达，男，毕业于华中科技大学，中国联通厦门分公司高级工程师。