当我们做完基因、RNA等芯片之后通常会拿到一组特别恐怖的数据,几百个基因几×几十个样本,这时候我想看这些基因的表达差异是否影响到样本的分布。可是有这么多基因,它们各自肯定都有影响,一个个看是不是很不现实。
比如这个样子,甲基化芯片检测了416个位点的甲基化程度,看不同样本间是否有差异。一共132个样本,分两组。
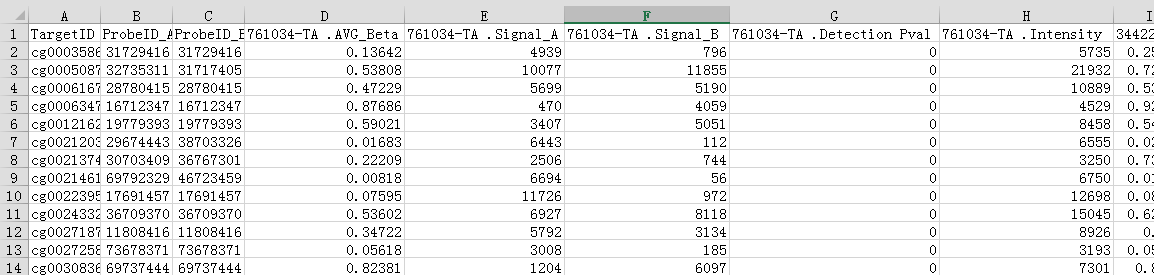
这当然只展示了一很小的部分。
每个样本由416个位点来描述,也就是416个变量,或叫416个维度。咱们生活的空间是3维的啊,如果要精确描述这132个样本的位置,就是建一个416维的空间把它们定位,这是很不现实的。所以要对它进行降维处理之后再观察。
主成分分析(PCA)就是常用的一种降维方法,提取出这么多变量中对样本影响最大的成分。但它不是挑选出某几个变量,而是根据它们的方差贡献,经过线性变换,得到新的变量,即“主成分”。
但再仔细观察,你会发现这表格的坑相当多,从代测公司拿回来就这样。我拉开展示变量名称的那几列,都只是在用不同的参数描述一个样本!
小数点前面是样本编号;小数点后面的Signal A是非甲基化等位基因密度(U),Signal B是甲基化等位基因密度(M),Beta值即甲基化水平值,Beta = M / (M+U+100),而Intensity就是Signal A + Signal B。
况且,它这样样本为行甲基化位点为列,做出来的PCA其实反应的是样本对不同位点甲基化水平的影响,这跟我们的研究目的是相反的,所以要把它倒过来。
你再仔细找找说不定还有缺失值,也有可能等你做了一半才发现,这都是惨淡的现实。
你已经能想到处理它要有多头痛了。不仅要提取每个样本的beta值那一列,还要把它的行和列翻转过来^0.0^我知道大家毕竟医学出身,对R语言代码有点怵,但如果表格简单一点、规模小一点,用SPSS也可以简单完成,但面对如此严酷的事实,咱们还是硬着头皮敲代码吧。其实做下来也不是那么难。
先检查一下缺失值,还都是beta值(唉我是做到一半才发现的,不得不倒回来处理)。在Excel中打开表格,全选,Ctrl+G,在弹出的对话框中点定位条件,查找空值:
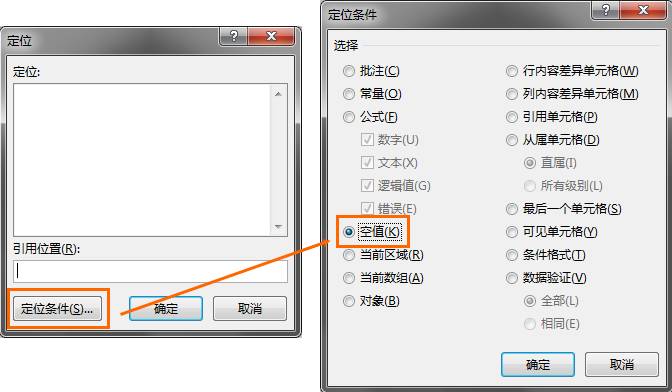
确定之后会自动选中缺失值的单元格,我们随便填个颜色标注出来。处理缺失值的一般方法,可以删除那个样本,或者以均值或中值填充。但既然在本案例中我们知道它的含义,而且有条件算出来,那我还是计算一下吧。
找到一个填了颜色的空值,在其中按Excel格式输入公式,使其符合beta值的计算方法,比如D82的空值就应该输入“=F82/(E82+F82+100)”,然后选中该单元格并Ctrl+C,保持它被选中有虚线围绕的状态。
然后再做一次找空值的操作,这回可以全选表格来查找,也可以只选中有数据的表格(因为后面有几列是跟PCA无关的内容)。找到空值之后Ctrl+V,就把刚才的公式填上了。这样就可以导入RStudio。
下面,书写的格式,就按R中的习惯吧,“##”后面的文字是大步骤,“#”后面的文字是对上一行代码的注释
## 准备工作环境
rm(list = ls())
# 把工作空间先清理干净
setwd("D:/PCA")
# 设置工作目录
library(pca3d)
library(rgl)
library(readxl)
# 载入以上这些R包。如果你还没安装,就先用install.packages(‘包的名称’)装上,再运行library()。装包的时候好像要翻墙,其他时候不用。
Raw
# 用read_excel()函数读取原Excel文件,并把它命名为Raw。其实也可以从菜单“File→Import Dataset→From Excel”导入,反正也是调用这个函数。随意啦。
这样就可以在Environment选项卡中看到这个超大的表格。以后操作过程中可以随时观察这个选项卡中添加了哪些元素。
## 提取所需数据
num
# 定义我们需要的大表格中列的编号。回去观察那个大表,第一个样本的beta值在第4列,所有芯片数据的最后一列是第663列,是个Intensity,from和to就是选定这个范围。我们需要的是beta值,每隔5列出现一个,所以by=5。同理,如果我们需要的是single_A,那么from=5。
Data
# 把从大表格中提取出来的小表格命名为Data。后面的[,num]就是刚才挑选的列号了。
DataRev
# 把小表格的行和列翻转过来,形成一个新的表,命名为DataRev。可以在Environment中可以点击各表查看效果。
Group
# 因为患者的个体编号和分组编号混起来了,所以我们要另外添加一列Group,表示分组。这是定义Group的内容,66个Ca(癌组织)和66个NA(癌旁组织)。
DataRevG
# 把上面的Group添加到DataRev表中,形成的新表命名为DataRevG。
到这里,准备工作才做完。
## 主成分分析
DataRevG_sub
# 因为PCA是不需要Group那列的,那是为将来绘图准备的,所以要建一个子表,把那列减去,命名为新表,原名加上后缀_sub。
DataRevG.pca
# 用prcomp()函数对那个子表做分析,并把结果拎出来,命名为DataRevG.pca的一个大集合。
Pca.sum
# 对PCA结果做描述性分析,命名为pca.sum。可以从这里查看分析的各项结果。
Importance
# 提取pca.sum中的Importance,独立出来成为一个叫Importance的新数据框,它展示的是主成分的重要度。其实不提取也可以,但提出来是为了方便观察。点开它可以看到,它分为标准差、方差贡献率、累积贡献率三行。我们主要看累积贡献率。

PC1是第一个主成分(Principal Component),它的贡献率是30.51%,PC2贡献了8.95%,两者累积39.46%,依此累推。这就决定我们选取几个主成分来观察样本。一般来说,选取累积贡献率达到80%-90%的前几个,有时候2个就满足了,可以做个二维图,不行就三维。
但本例中有点意外,前3个PC贡献率并没有那么高,说明影响较大的主成分比较多。这时可以画个碎石图来观察主成分的分布规律。
screeplot(DataRevG.pca, type = 'line', lwd = 2)
# 画碎石图,type就是碎石图的类型,lwd是线宽。
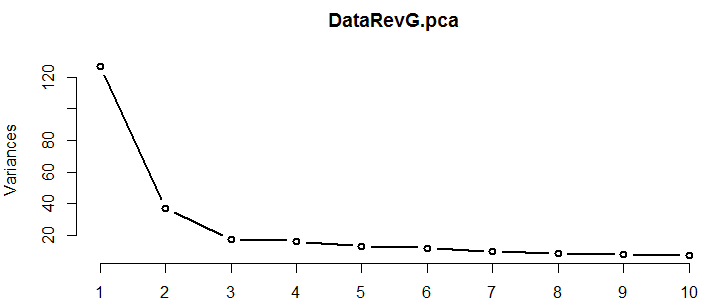
这样看来,第三个主成分之后,方差贡献趋于平缓,那我们还是选取前三个来作图分析。
## 作图
open3d()
# 打开3D图形窗口。
par3d(windowRect = c(100, 100, 612, 612))
# 重设窗口大小。
pca3d(DataRevG.pca, components = 1:3, group = DataRevG$Group, col = c('Ca' = 'light blue', 'NA' = 'yellow'), show.axes = T, show.axe.titles = F, shape = 'sphere', show.plane = F)
# 画散点图。Componets选第1-3个,group则按DataRevG中的Group这一列来分,col是分别给每组的样本选个颜色,show.axes是显示坐标轴,T是指True,即显示,后面的是坐标轴名,F自然就是False不显示了。这些都可根据自己的喜好设置,更详细的参数可以在RStudio的Help中搜索函数名pca3d来查看。
axes3d(edges = 'bbox', labels = T, box = F)
# 给图加个带坐标的边框。
legend3d("topright", legend = c('Ca','NA'), col = c('light blue','yellow'), pch = 16, cex = 1, inset = c(0.02))
# 加上图例。注意颜色和组名的顺序要跟上面作图时一致。
好了,终于可以看效果了:
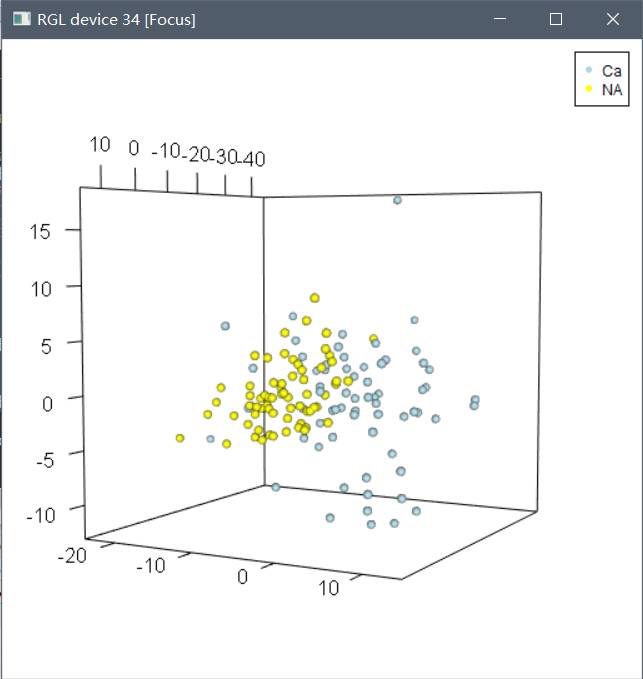
在这个小窗口里,3D图是可以旋转的。找到个好角度,就可以截图下来了。截图,当然不是用日常工具了~用下面这个函数,截成期刊需要的格式:
rgl.postscript('Example.eps', fmt = 'eps', drawText = T)
# 这是截成eps格式。另外也支持ps、tex、pdf、svg、pgf这些优质图片的格式。就是截出来的矢量图文件有点大。
就这样做好了。





